Конспект. конспекты по Астрономии. 1. звезды и созвездия,небесные координаты и звездные карты

• Название: 1. звезды и созвездия,небесные координаты и звездные карты
• Анкор: Конспект
• Дата: 06.02.2023
• Размер: 50.56 Kb.
• Имя файла: конспекты по Астрономии.odt
• Тип: Поэма; #922391

Астрономия . Беседин Павел 131 группа

Тема : 1. звезды и созвездия ,небесные координаты и звездные карты .

Многие характерные «звёздные фигуры» уже в глубокой древности получили имена героев греческих мифов и легенд, а также тех мифических существ, с которыми эти герои сражались. Так появились на небе Геркулес, Орион, Персей, Андромеда, а также Дракон, Телец, Кит. Некоторые из этих созвездий упоминаются в древнегреческих поэмах «Илиада» и «Одиссея». Их изображения можно видеть в старинных звёздных атласах, на глобусах и картах звёздного неба

В наши дни созвездиями называются определённые участки звездного неба, разделенные между собой строго установленными границами.

Все звёзды, видимые на небе невооружённым глазом, Гиппарх во II в. до н. э. разделил на шесть величин. Самые яркие (их на небе менее 20) стали считать звёздами первой величины. Чем слабее звезда, тем больше число, обозначающее её звёздную величину.В каждом созвездии звёзды обозначаются буквами греческого алфавита (приложение II), как правило, в порядке убывания их яркости. Наиболее яркая в этом созвездии звезда обозначается буквой а, вторая по яркости — β и т. д. Кроме того, примерно 300 звёзд получили собственные имена арабского и греческого происхождения.Впоследствии учёные стали располагать фотометрами для измерения освещённости, т. е. потока излучения, приходящего от звезды (или другого источника) к наблюдателю в единицу времени на единицу площади, перпендикулярной лучу зрения.Современная шкала звёздных величин определена так, что звезда первой величины в 2,512 раза ярче звезды второй величины ,самая яркая звезда ночного неба — Сириус (α Большого Пса) получила даже отрицательную звёздную величину —1,5.

2.Небесные координаты и звёздные карты

Невооружённым глазом на всём небе можно видеть примерно 6000 звёзд, но мы видим лишь половину из них, потому что другую половину звёздного неба закрывает от нас Земля. Вследствие её вращения вид звёздного неба меняется. На снимке каждая звезда оставила свой след в виде дуги окружности Общий центр всех этих концентрических дуг находится на небе неподалёку от Полярной звезды. Эта точка, в которую направлена ось вращения Земли, получила название Северный полюс мира.

Ведь сутки — это период полного оборота Земли вокруг своей оси. За час Земля повернётся на 1/24 часть окружности, т. е. на 15°. Следовательно, длина дуги, которую звезда опишет за это время, составит 15°, а за полчаса — 7,5°.Для указания положения светил на небе используют систему координат, аналогичную той, которая используется в географии, — систему экваториальных координат.

Географическая долгота (λ) отсчитывается вдоль экватора от начального (Гринвичского) меридиана, а географическая широта (φ) — по меридианам от экватора к полюсам Земли. Так, например, Москва имеет следующие координаты: 37°30' восточной долготы и 55°45' северной широты.Вторая координата, которая указывает положение светила на небе, аналогична географической долготе. Эта координата называется прямым восхождениеми обозначается буквой α. Прямое восхождение отсчитывается по небесному экватору от точки весеннего равноденствия  в которой Солнце ежегодно бывает 21 марта (в день весеннего равноденствия). В астрономии принято выражать прямое восхождение не в градусной мере, а в часовой. Вы помните, что вследствие вращения Земли 24 ч соответствуют 360°, а 1 ч — 15°. Следовательно, прямое восхождение, равное, например, 12 ч, составляет 180°, а 7 ч 40 мин соответствует 115°.В зависимости от звёздной величины звёзды изображают на карте кружками различного диаметра. Те из них, которые образуют характерные фигуры созвездий, соединены сплошными линиями. Границы созвездий обозначены пунктиром.

Тема:Видимое движение звёзд на различных географических широтах :Годичное движение Солнца по небу. Эклиптика

Ещё в глубокой древности, наблюдая за Солнцем, люди обнаружили, что его полуденная высота в течение года меняется, как меняется и вид звездного неба: в полночь над южной частью горизонта в различное время года видны звёзды разных созвездий — те, которые видны летом, не видны зимой, и наоборот.Круг небесной сферы, по которому происходит видимое годичное движение Солнца, назвали эклиптикой.

Созвездия, по которым проходит эклиптика, получили название зодиакальных(от греч. «зоон» — животное). Каждое зодиакальное созвездие ,перемещение Солнца на фоне звёзд — явление кажущееся. Происходит оно вследствие годичного обращения Земли вокруг Солнца . Поэтому эклиптика представляет собой тот круг небесной сферы, по которому она пересекается с плоскостью земной орбиты. Солнце поднимается над плоскостью земного (и небесного) экватора на 23°26'. В день зимнего солнцестояния (22 декабря), когда Северное полушарие освещается хуже всего, Солнце находится ниже небесного экватора на такой же угол 23°26'.В зависимости от положения Солнца на эклиптике меняется его высота над горизонтом в полдень — момент верхней кульминации. Измерив полуденную высоту Солнца и зная его склонение в этот день, можно вычислить географическую широту места наблюдения. Этот способ издавна использовался для определения местоположения наблюдателя на суше и на море.

1.Движение и фазы Луны

Луна — ближайшее к Земле небесное тело, её единственный естественный спутник. Находясь на расстоянии около 380 тыс. км от Земли, Луна обращается вокруг неё в том же направлении, в котором Земля вращается вокруг своей оси. За каждые сутки она перемещается относительно звёзд примерно на 13°, совершая полный оборот за 27,3 суток. Этот промежуток времени — период обращения Луны вокруг Земли в системе отсчёта, связанной со звёздами, — называется звёзднымили сидерическим(от лат. sidus — звезда) месяцем.Собственного свечения Луна не имеет, а Солнце освещает только половину лунного шара. Поэтому по мере её движения по орбите вокруг Земли происходит изменение вида Луны — смена лунных фаз.Если она расположена так, что обращена к Земле своей тёмной, неосвещённой стороной (положение 1), то мы не можем видеть Луну, но знаем, что она находится на небе где-то рядом с Солнцем. Эта фаза Луны называется новолунием.Через неделю после новолуния мы видим половину освещенного полушария Луны — наступает фаза, называемая первой четвертью . В дальнейшем доля освещённого полушария Луны, видимая с Земли, продолжает увеличиваться до тех пор, пока не наступит полнолуние , а через неделю после полнолуния наступает фаза последней четверти . В последующем её серп, обращённый теперь выпуклостью влево (если смотреть из Северного полушария Земли), становится всё более и более узким , постепенно сближаясь с Солнцем. В конце концов он скрывается в лучах восходящего Солнца — снова наступает новолуние.Полный цикл смены лунных фаз составляет 29,5 суток. Этот промежуток времени между двумя последовательными одинаковыми фазами называется синодическим месяцем(от греч. synodos — соединение). Ещё в глубокой древности у многих народов месяц, наряду с сутками и годом, стал одной из основных календарных единиц.

2.Затмения Солнца и Луны

Как и любые физические тела, находящиеся недалеко от Солнца, Земля и Луна отбрасывают в противоположную от него сторону тени. Периодически во время новолуния может наступить ситуация, когда тень Луны попадет на Землю, и тогда в данной части нашей планеты произойдёт солнечное затмение — Луна заслонит Солнце. В полнолуние, наоборот, Луна может попасть в тень Земли, что вызовет потемнение яркого диска Луны. В этом случае говорят о лунном затмении.

В том случае, если Солнце целиком закрыто Луной, затмение называется полным. Если же случится так, что она закроет лишь часть Солнца, то затмение будет частным. Из-за небольшого изменения расстояний до Солнца и Луны может сложиться ситуация, что центры их видимых дисков на небе совпадают, но видимые размеры Луны окажутся чуть меньше, и она не закроет Солнце целиком, оставив от него яркое тонкое кольцо.

Такое затмени называется кольцеобразным.Полная фаза затмения длится около полутора часов. Путь, который проходит тень Луны, называется полосой полного солнечного затмения .Располагая необходимыми данными о предстоящих затмениях, учёные получают возможность организовать экспедиции в полосу полного солнечного затмения. В момент полной фазы можно наблюдать внешние, наиболее разреженные слои атмосферы Солнца — солнечную корону, которая в обычных условиях с поверхности Земли не видна. В прошлом многие важные сведения о природе Солнца были получены именно во время полных затмений.

Время и календарь

Солнце всегда освещает только половину земного шара: на одном полушарии — день, а на другом в это время ночь, соответственно всегда есть точки, где в данный момент полдень и Солнце находится в верхней кульминации. По мере того как Земля вращается вокруг оси, полдень наступает в тех местах, которые лежат всё западнее. По положению Солнца (или звёзд) на небе определяется местное время для любой точки земного шара. Местное время в двух пунктах (T₁ и Т₂) отличается ровно на столько, на сколько отличается их географическая долгота:

Т₁ - Т₂ = λ₁ - λ₂.

Ясно, что полдень наступает в данном пункте Земли позже, чем в другом, ровно на столько, сколько времени нужно планете, чтобы повернуться на угол, соответствующий разности их долгот. Так, например, в Санкт-Петербурге, который находится на 8°45' западнее Москвы, полдень наступает на 35 мин позднее.

Определив из наблюдений местное время в данном пункте и сравнив его с местным временем другого, географическая долгота которого известна, можно вычислить географическую долготу пункта наблюдения. Условились отсчитывать долготу от начального (нулевого) меридиана, проходящего через Гринвичскую обсерваторию. Местное время этого меридиана называют всемирным временем — Universal Time (UT). Тогда

Т₁ = UT + λ₁,

иначе говоря, местное время любого пункта равно всемирному времени в этот момент плюс долгота данного пункта от начального меридиана, выраженная в часовой мере.

Если бы в своей повседневной жизни мы пользовались местным временем, то по мере передвижения на запад или восток приходилось бы непрерывно передвигать стрелки часов. Возникающие при этом неудобства столь очевидны, что в настоящее время практически всё население земного шара пользуется поясным временем.Местное время основного меридиана данного пояса называется поясным временем.В нашей стране поясное время было введено с 1 июля 1919 г. С тех пор границы часовых поясов неоднократно пересматривались и изменялись.

 Тема : Время и Календарь

Система счёта длительных промежутков времени, согласно которой устанавливается определённая продолжительность месяцев, их порядок в году и начальный момент отсчёта лет, называется календарём.Уже на первом этапе развития цивилизации некоторые народы стали пользоваться лунными календарями. В этих календарях чередовались месяцы продолжительностью 29 и 30 суток.Двенадцать лунных месяцев содержат всего 354 дня.Тропический годсоставляет 365 суток 5 часов 48 минут 46,1 секунды.Непосредственный предшественник современного календаря был разработан в Древнем Риме по приказу императора Юлия Цезаря и потому получил название юлианского. Год, согласно этому календарю, состоял из 12 месяцев и содержал 365 или 366 суток. Лишние сутки добавлялись каждые четыре года: такие годы, номер которых делится на четыре, получили название високосных.С учётом високосных лет продолжительность года по юлианскому календарю (старому стилю) отличалась от продолжительности тропического года на 11 минут 14 секунд, что давало ошибку в 1 сутки за 128 лет, или 3 суток примерно за 400 лет. Юлианский календарь был принят в качестве христианского в 325 г. н. э., и ко второй половине XVI в. расхождение достигло уже 10 суток.Для того чтобы исправить расхождение, папа римский Григорий XIII в 1582 г. ввёл новый стиль, календарь, названный по его имени григорианским. Чтобы уменьшить отличие календарного года от тропического, было решено каждые 400 лет выбрасывать из счёта 3 суток путём сокращения числа високосных лет. Простыми, невисокосными условились считать все годы столетий, за исключением тех, у которых число столетий делится на 4 без остатка. Високосным считались 1600 и 2000 гг. В то же время 1700, 1800 и 1900 гг. были простыми.Нумерация лет как по новому, так и по старому стилю ведётся от года Рождества Христова, наступления новой эры. В России новая эра была введена указом Петра I, согласно которому после 31 декабря 7208 г. «от сотворения мира» наступило 1 января 1700 г. от Рождества Христова.
 Тема:Развитие представлений о строении мира

1.Геоцентрическая система мира

Путь к пониманию положения нашей планеты и живущего на ней человечества во Вселенной был очень непростым и подчас весьма драматичным. В древности было естественным считать, что Земля является неподвижной, плоской и находится в центре мира. Казалось, что вообще весь мир создан ради человека. Подобные представления получили название антропоцентризма (от греч. antropos — человек).

Многие идеи и мысли, которые в дальнейшем отразились в современных научных представлениях о природе, в частности в астрономии, зародились в Древней Греции, еще за несколько веков до нашей эры. Трудно перечислить имена всех мыслителей и их гениальные догадки. Выдающийся математик Пифагор (VI в. до н. э.) был убеждён, что «в мире правит число».Другой не менее известный учёный древности, Демокрит — основоположник представлении об атомах, жившии за 400 лет до нашей эры, — считал, что Солнце во много раз больше Земли, что Луна сама не светится, а лишь отражает солнечный свет, а Млечный Путь состоит из огромного количества звёзд.

Обобщить все знания, которые были накоплены к IV в. до н. э., смог выдающийся философ античного мира Аристотель (384—322 до н. э.). Его деятельность охватывала все естественные науки — сведения о небе и Земле, о закономерностях движения тел, о животных и растениях и т. д.

Планеты размещены на особых сферах, которые вращаются вокруг Земли. Такая система мира получила название геоцентрической  Среди учёных древности выделяется смелостью своих догадок Аристарх Самосский, живший в III в. до н. э. Он первым определил расстояние до Луны, вычислил размеры Солнца, которое, по его данным, оказалось в 300 с лишним раз больше Земли по объёму. Вероятно, эти данные стали одним из оснований для вывода о том, что Земля вместе с другими планетами движется вокруг этого самого крупного тела. В наши дни Аристарха Самосского стали называть «Коперником античного мира».

2.Гелиоцентрическая система мира

Создание гелиоцентрической системы ознаменовало новый этап в развитии не только астрономии, но и всего естествознания. Особо важную роль сыграла идея Коперника о том, что за видимой картиной происходящих явлений, которая кажется нам истинной, надо искать и находить недоступную для непосредственного наблюдения сущность этих явлений.Гелиоцентрическая система мира, обоснованная, но не доказанная Коперником, получила своё подтверждение и развитие в трудах таких выдающихся учёных, как Галилео Галилей (1564—1642) и Иоганн Кеплер (1571— 1630).

Галилей, одним из первых направивший телескоп на небо, истолковал сделанные при этом открытия как доводы в пользу теории Коперника. Открыв смену фаз Венеры, он пришёл к выводу, что такая их последовательность может наблюдаться только в случае её обращения вокруг Солнца. Обнаруженные им четыре спутника планеты Юпитер также опровергали представления о том, что Земля является единственным в мире центром, вокруг которого может происходить вращение других тел. Галилей не только увидел горы на Луне, но даже измерил их высоту. Наряду с несколькими другими учёными он также наблюдал пятна на Солнце и заметил их перемещение по солнечному диску. На этом основании он заключил, что Солнце вращается и, следовательно, имеет такое движение, которое Коперник приписывал нашей планете. Так был сделан вывод о том, что Солнце и Луна имеют определённое сходство с Землёй. Наконец, наблюдая в Млечном Пути и вне его множество слабых звёзд, недоступных невооруженному глазу, Галилеи сделал вывод о том, что расстояния до звезд различны и никакой «сферы неподвижных звёзд» не существует. Все эти открытия стали новым этапом в осознании положения Земли во Вселенной.

Тема:Конфигурация планет. Синодический период

1Конфигурация планет и условия их видимости

Условия видимости планет1 меняются по-разному: если Меркурий и Венеру можно видеть только утром или вечером, то остальные — Марс, Юпитер и Сатурн — бывают видны также и ночью. По временам одна или несколько планет могут быть вовсе не видны, поскольку они располагаются на небе поблизости от Солнца. В этом случае говорят, что планета находится в соединении с Солнцем. Если же планета располагается на небе вблизи точки, диаметрально противоположной Солнцу, то она находится в противостоянии.  Соединение и противостояние, а также другие характерные расположения планеты относительно Солнца называются конфигурациями. Единственной конфигурацией, в которой может находиться любая планета, независимо от того, внутренняя она или внешняя, является верхнее соединение.  Внутренняя планета может оказаться между Солнцем и Землей, и тогда говорят о ее нижнем соединении с Солнцем. Внешняя планета может находиться на любом угловом расстоянии от Солнца (от 0 до 180°). Когда оно составляет 90°, то говорят, что планета находится в квадратуре. Для внутренних планет максимально возможное угловое удаление от Солнца (в элонгации) невелико: для Венеры — до 47°, а для Меркурия — всего 28°.

Конфигурации планеты периодически повторяются.

Промежуток времени между двумя последовательными одноимёнными конфигурациями планеты (например, верхними соединениями) называется её синодическим периодом.

Период обращения планеты вокруг Солнца по отношению к звёздам называется звёздным (или сидерическим) периодом. Рассмотрим, как связан синодический период планеты со звёздными периодами Земли и самой планеты. Чем ближе планета к Солнцу, тем быстрее она совершает свой оборот вокруг него. Пусть звёздный период обращения внешней планеты равен Р, звёздный период Земли — T(T < Р), а синодический период — S. Тогда угловые скорости их движения по орбитам будут равны соответственно 360°/P и 360°/T. От момента какой-либо конфигурации (например, противостояния) до следующей такой же конфигурации планета пройдет дугу своей орбиты, равную   За этот же промежуток времени (за синодический период) Земля пройдёт дугу на 360° большую, которая равна   Тогда:

или

Почти такой же будет формула для внутренней планеты:

Следовательно, зная синодический период планеты, можно вычислить ее звездный период обращения вокруг Солнца.

Законы движения планет Солнечной системы

 Законы движения планет, которые были открыты Иоганном Кеплером и стали первыми естественно-научными законами в их современном понимании. Многие учёные вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой — окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Чтобы построить орбиту Марса, он применил способ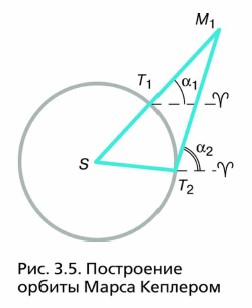


Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение α1, которое выражается углом  Т1M1, где Т1 — положение Земли на орбите в этот момент, а M1 — положение Марса. Очевидно, что спустя 687 суток (таков звёздный период обращения Марса) планета придёт в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости её орбиты. Земля в этот момент находится в точке Т2, и, следовательно, угол  Т2М1 есть не что иное, как прямое восхождение Марса — α2. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил ещё целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты. Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этом

радиус-вектор планеты за равные промежутки времени описывает равные площади.

Впоследствии эта закономерность получила название второго закона Кеплера.

Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиусом-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АA₁, ВВ₁, и СС₁ — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.

В результате был сформулирован закон, который называется первым законом Кеплера.

Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

Пример решения задачи

Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?



 Определение расстояний и размеров тел в Солнечной системе :1. Форма и размеры Земли

Считается, что первое достаточно точное определение размеров Земли провёл греческий учёный Эратосфен(276— 194 до н. э.), живший в Египте. Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину её радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: φB — φA.

Обозначив длину окружности земного шара через L, получим такое выражение:

откуда следует, что длина окружности земного шара равняется 250 тыс. стадий.

Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.

В настоящее время форму Земли принято характеризовать следующими величинами:

сжатие эллипсоида — 1 : 298,25;

средний радиус — 6371,032 км;

длина окружности экватора — 40075,696 км.

2.Определение расстояний в Солнечной системе. Горизонтальный параллакс

Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца.

Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).



Из треугольника OAS можно выразить величину — расстояние OS = D:

где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.

Известно, что для малых углов sin р ≈ р, если угол р выражен в радианах. В одном радиане содержится 206 265". Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:

или (с достаточной точностью)

Пример решения задачи

На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9"?

3.Определение размеров светил

Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12). Формула, связывающая эти величины, аналогична формуле для определения параллакса:

Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30', а все планеты видны невооруженным глазом как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:

Следовательно,

Если расстояние D известно, то

r = Dρ,

где величина р выражена в радианах.

Пример решения задачи

Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30'?



 Движение небесных тел под действием сил тяготения
1.Закон всемирного тяготения

Согласно закону всемирного тяготения, изученному в курсе физики,

все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

где m₁ и m₂ — массы тел; r — расстояние между ними; G — гравитационная постоянная.

Исааку Ньютону (1643—1727) доказать тождественность силы, удерживающей Луну при ее движении вокруг Земли, и силы, вызывающей падение тел на Землю.

Ведь если сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна, находящаяся от Земли на расстоянии примерно 60 её радиусов, должна испытывать ускорение в 3600 раз меньшее, чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с². Следовательно, ускорение Луны должно составлять 0,0027 м/с².

В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение

а = ω²r,

где ω — угловая скорость Луны; r — радиус её орбиты. Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять r = 60 • 6 400 000 м = 3,84 • 10⁸ м. Звёздный период обращения Луны Т = 27,32 суток, в секундах составляет 2,36 • 10⁶ с. Тогда ускорение орбитального движения Луны

Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.

Можно убедиться и в том, что при движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения. Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит d и квадратов периодов обращения Т есть величина постоянная:

Ускорение планеты равно

Из третьего закона Кеплера следует

поэтому ускорение планеты равно

Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения

2.Возмущения в движении тел Солнечной системы

Законы Кеплера строго выполняются, если рассматривается движение двух изолированных тел (Солнце и планета) под действием их взаимного притяжения. Однако в Солнечной системе планет много, все они взаимодействуют не только с Солнцем, но и между собой. Поэтому движение планет и других тел не в точности подчиняется законам Кеплера. Отклонения тел от движения по эллипсам называются возмущениями.

Вильям Гершель в 1781 г. открыл планету, названную впоследствии Ураном

 На основе расчётов Леверье немецкий астроном Иоганн Галле 23 сентября 1846 г. обнаружил в созвездии Водолея неизвестную ранее планету — Нептун. 

В 1930 г. после просмотра большого количества фотографий звёздного неба был обнаружен Плутон, который, как оказалось, является одним из множества объектов, расположенных за орбитой Нептуна.

3.Масса и плотность Земли

Закон всемирного тяготения позволил определить массу нашей планеты. Исходя из закона всемирного тяготения, ускорение свободного падения можно выразить так:

Подставим в формулу известные значения этих величин: g = 9,8 м/с², G = 6,67 • 10^-11 Н • м²/кг², R = 6370 км — и получим, что масса Земли М = 6 • 10²⁴ кг.

Зная массу и объём земного шара, можно вычислить его среднюю плотность: 5,5 • 10³ кг/м³. С глубиной за счёт увеличения давления и содержания тяжелых элементов плотность возрастает.

 

4.Масса и плотность Земли

Более точная формула третьего закона Кеплера, которая была получена Ньютоном, даёт возможность определить одну из важнейших характеристик любого небесного тела — массу. Выведем эту формулу, считая (в первом приближении) орбиты планет круговыми.

Пусть два тела, имеющие массы m₁, и m₂, взаимно притягивающиеся и обращающиеся вокруг общего центра масс, находятся от центра масс на расстоянии r₁ и r₂ и обращаются вокруг него с периодом Т. Расстояние между их центрами R = r₁ + r₂. На основании закона всемирного тяготения ускорение каждого из этих тел равно:

Угловая скорость обращения вокруг центра масс составляет   Тогда центростремительное ускорение выразится для каждого тела так:

Приравняв полученные для ускорений выражения, выразив из них r₁, и r₂ и сложив их почленно, получаем:

откуда

Поскольку в правой части этого выражения находятся только постоянные величины, оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, — Солнце и планета, планета и спутник. Определим массу Солнца, для этого запишем выражение:

где М — масса Солнца; m₁ — масса Земли; m₂ — масса Луны; Т₁ и a₁ — период обращения Земли вокруг Солнца (год) и большая полуось её орбиты; Т₂ и а₂ — период обращения Луны вокруг Земли и большая полуось лунной орбиты.

Пренебрегая массой Земли, которая ничтожно мала по сравнению с массой Солнца, и массой Луны, которая в 81 раз меньше массы Земли, получим:

Подставив в формулу соответствующие значения и приняв массу Земли за единицу, мы получим, что Солнце примерно в 333 тыс. раз по массе больше нашей планеты.

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях.