110. Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение аτточки, если известно, что за время T = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение аn=2,7 м/с2.
R = 30 см
aτ = const
T= 4 с
N(T) = 3
аn=2,7 м/с2
|
На рисунке показаны направления тангенциального aτ, нормального an ускорений и полного ускорений точки.
П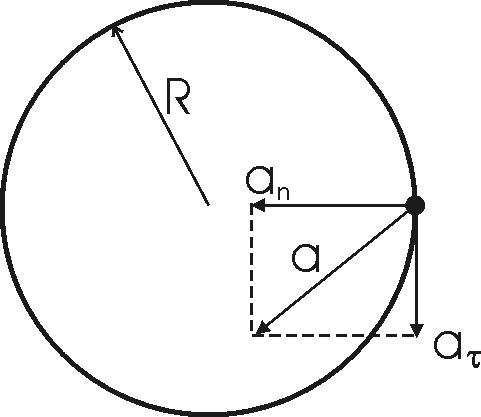 о определению нормальное ускорение о определению нормальное ускорение 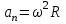 , где ω – угловая скорость точки, R - радиус. Откуда , где ω – угловая скорость точки, R - радиус. Откуда 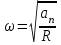 . .
Угловая скорость с другой стороны равна ω=ω0+εt. Откуда 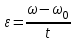 . .
По определению тангенциальное ускорение 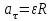 , где ε – угловое ускорение точки. , где ε – угловое ускорение точки.
Зависимость угла поворота от времени: 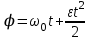 . Поэтому число оборотов равно . Поэтому число оборотов равно 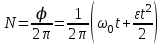 . Подставляем сюда . Подставляем сюда 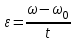 и получаем и получаем 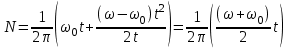 . Откуда . Откуда 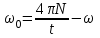 . Подставляем в . Подставляем в 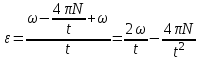 . .
Нам уже известно, что 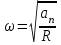 , поэтому через время T угловое ускорение , поэтому через время T угловое ускорение 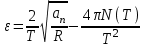 . Тогда искомая величина . Тогда искомая величина
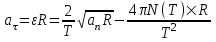 . Подставляем числа. . Подставляем числа.
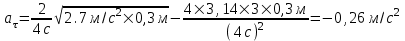 . .
|
aτ = ?
|
128. Шар массой m = 5 кг движется со скоростью V0 = 1 м/с и сталкивается с покоящимся шаром массой M = 2 кг. Определить скорости V1 и V2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
m = 5кг
V0 = 1 м/с
M = 2 кг
|
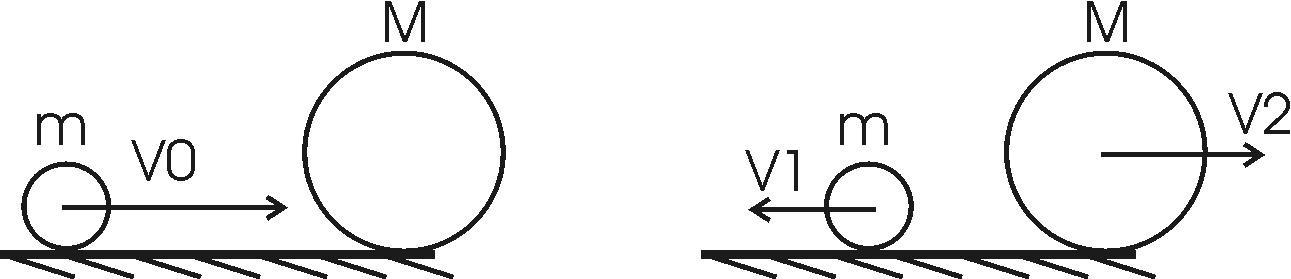
Шарики должны отскочить в разные стороны так как удар упругий, поэтому из закона сохранения импульса находим: 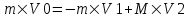 . .
Из закона сохранения энергии получаем: 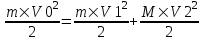 . .
Из первого уравнения находим скорость второго шара 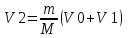 . Подставляем во второе уравнение: . Подставляем во второе уравнение: 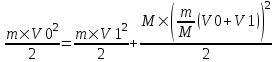 . Упрощаем: . Упрощаем: 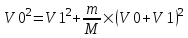 . Далее . Далее 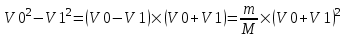 , откуда получаем , откуда получаем 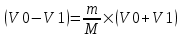 . И, наконец, находим скорость первого шара после удара: . И, наконец, находим скорость первого шара после удара: 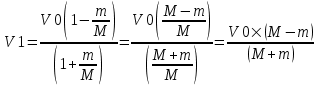 . Подставляем в . Подставляем в 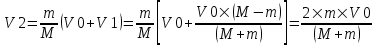 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ). 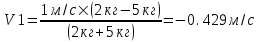 . Эта величина отрицательная, следовательно, вектор V1 должен быть направлен в противоположную сторону. . Эта величина отрицательная, следовательно, вектор V1 должен быть направлен в противоположную сторону.
Находим скорость второго шара: 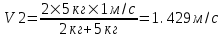 . .
|
V1 = ?
V2 = ?
|
140. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой H = 40 м, наружным диаметром D=3,0 м и внутренним диаметром d = 2,0 м? Плотность материала ρ принять равной 2,8×103кг/м3.
H = 40 м
D=3,0 м
d = 2,0 м
ρ= 2,8×103кг/м3
|
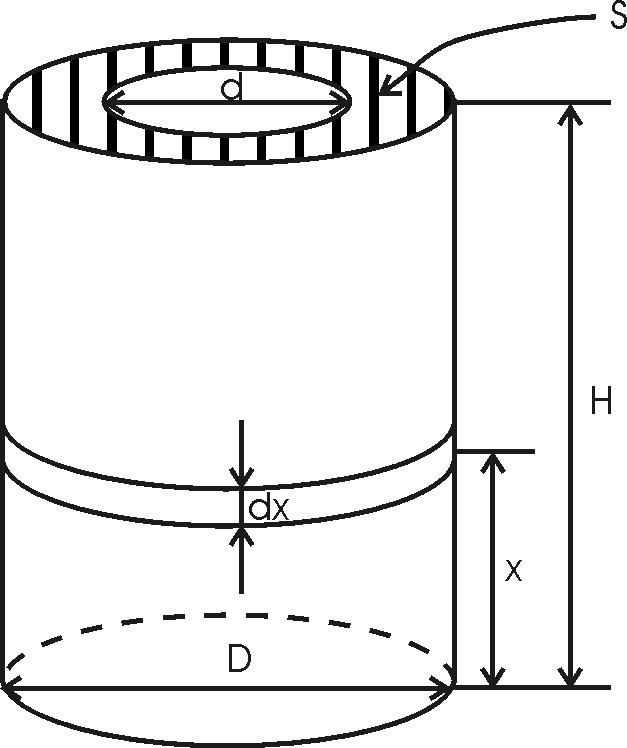
Найдем потенциальную энергию тонкого слоя dx, находящегося на высоте x. Для этого нам нужно узнать массу этого слоя. Она равна dm=ρ×dV, где ρ – плотность материала, dV=S×dx – объем этого слоя.
Тогда dm=ρ×S×dx. Откуда потенциальная энергия равна 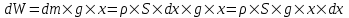 . Проинтегрируем правую и левую части: . Проинтегрируем правую и левую части: 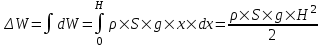 . .
Площадь кольца равна (см. рис) 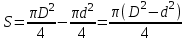 . Поэтому потенциальная энергия установки, равная совершенной работе: . Поэтому потенциальная энергия установки, равная совершенной работе:
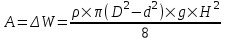 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ).
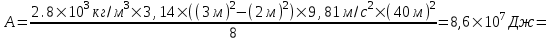
=86МДж.
|
A = ?
|
142. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение ε и частоту вращения ν маховика через время t= 10 с после начала действия силы, если радиус R шкива равен 12 см. Силой трения пренебречь.
D = 75 см
m = 40 кг
F = 1 кН
t= 10 с
R = 12 см
|
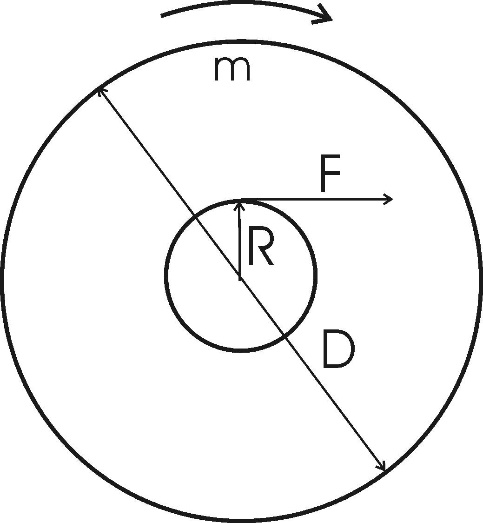
Из второго закона Ньютона, применяемого к вращающимся телам находим 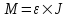 , где M – вращающий момент, ε – угловое ускорение, J – момент инерции диска. Момент инерции однородного диска массой m и диаметром D равен , где M – вращающий момент, ε – угловое ускорение, J – момент инерции диска. Момент инерции однородного диска массой m и диаметром D равен 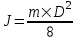 . Так как сила приложена к краю шкива, то вращающий момент этой силы равен M=F×R. Откуда угловое ускорение . Так как сила приложена к краю шкива, то вращающий момент этой силы равен M=F×R. Откуда угловое ускорение 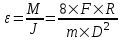 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 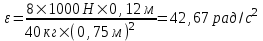 . .
Если диск вращается равноускоренно, то уравнение вращения 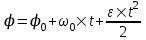 . Примем начальные условия . Примем начальные условия 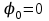 и и 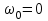 - так как начальная частота вращения равна нулю. Тогда - так как начальная частота вращения равна нулю. Тогда 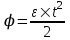 . .
По определению угловая скорость это производная угла поворота от времени 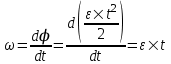 . Поэтому через время t=T угловая скорость равна . Поэтому через время t=T угловая скорость равна 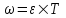 . Подставляем сюда . Подставляем сюда 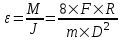 и получаем и получаем 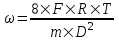 . Частота вращения равна по определению . Частота вращения равна по определению 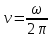 , поэтому , поэтому 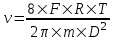
Подставляем числа. 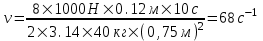 . .
|
ν = ?
ε = ?
|
155. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью ω1 станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол φ=90°? Момент инерции человека и скамьи J равен 2,5 кг×м2, момент инерции колеса J0=0,5кг×м2.
ω = 25 рад/с
J = 2,5 кг×м2
J0=0,5кг×м2
|
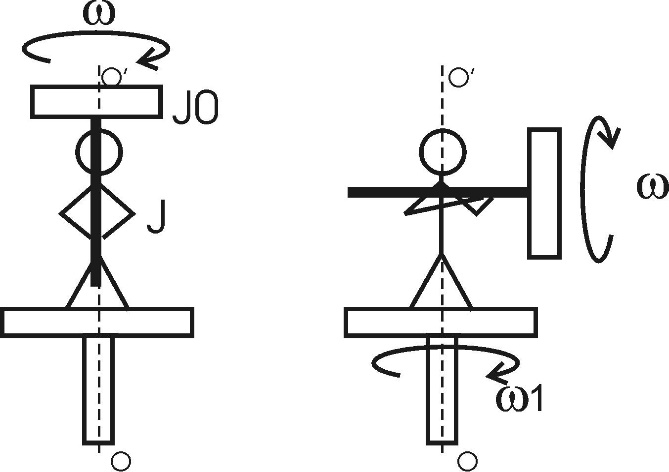
Из закона сохранения момента импульса имеем: в изолированной системе сумма моментов импульса всех тел – величина постоянная. Так как диск повернули на угол 90º, то проекция его момента импульса на ось OO’ равна нулю, поэтому 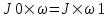 , где J0 - момент инерции диска, J – момент инерции скамьи с человеком относительно оси OO’. , где J0 - момент инерции диска, J – момент инерции скамьи с человеком относительно оси OO’.
Поэтому искомая величина 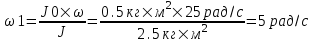 . .
|
ω1 = ?
|
162. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m = 2 кг: 1) с высоты h = 1000 км; 2) из бесконечности?
h1=R=1000км
h2 = ∞
m=2кг
M=6×1024 кг
|
На тело действует сила всемирного тяготения со стороны Земли, равная 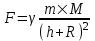 , где , где 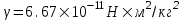 - гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли. - гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли.
Рассмотрим первый случай: h=1000км. Работа по определению равна 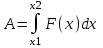 , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), 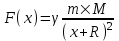 , а x – это положение (высота) тела. Тогда , а x – это положение (высота) тела. Тогда
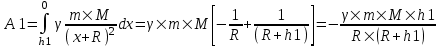 . Подставляем числа. . Подставляем числа. 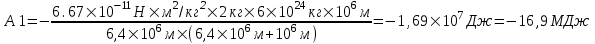 . .
Рассмотрим второй случай: h=∞.
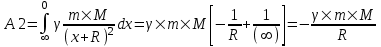 . .
Подставляем числа.
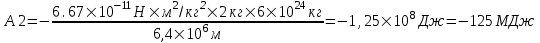 . .
|
A1 = ?
A2 = ?
|
172. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A1×sinω1×t и у=А2×cosω2×t, где A1 = 8 см, A2=4 см, ω1 = ω2=2с-1. Написать уравнение траектории и построить ее. Показать направление движения точки.
x=8sin2t см
y=4cos2t см
|
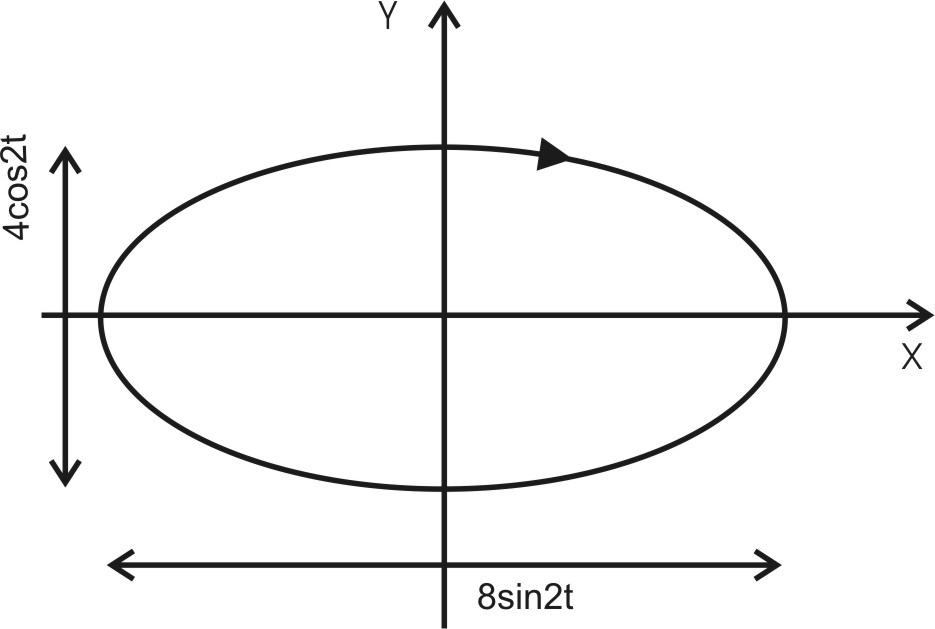
Видно, что 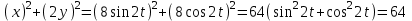 . .
Уравнение 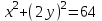 - это эллипс. По другому его записывают в виде - это эллипс. По другому его записывают в виде 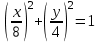 . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем: . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем:
x(t=0)=0см, а y(t=0)=4см. То есть точка находится на оси Y.
В момент t=π/2 получаем:
x(t= π/4)=8см, а y(t= π/4)=0см. То есть точка находится на оси X. Из этого делаем вывод, что точка движется от оси Y к оси X, то есть по часовой стрелке.
|
Траектория - ?
|
180. Шарик массой m=60 г колеблется с периодом T=2с. В начальный момент времени смещение шарика х0=4,0 см и он обладает энергией E=0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
m=60 г
х0=4 см
Т=2 с
E=0,02 Дж
|
Уравнение гармонических колебаний 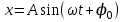 , где x – смещение колеблющейся величины, A – амплитуда колебаний, , где x – смещение колеблющейся величины, A – амплитуда колебаний, 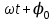 - фаза колебаний, - фаза колебаний, 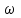 - циклическая частота, φ0 – начальная фаза. - циклическая частота, φ0 – начальная фаза.
Скорость равна 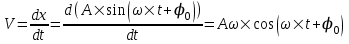 . .
В начальный момент t=0 имеем 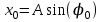 и и 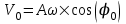 . Тогда начальная энергия равна . Тогда начальная энергия равна 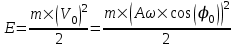 . .
Отношение 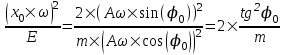 . .
Циклическая частота равна по определению 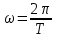 , где T – период. Поэтому , где T – период. Поэтому 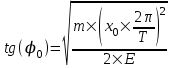 . .
Начальная фаза равна 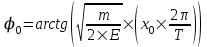 . Подставляем числа. . Подставляем числа. 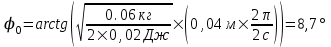 . .
Теперь найдем амплитуду. Умножим 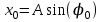 на на 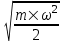 , возведем все в квадрат и сложим с , возведем все в квадрат и сложим с 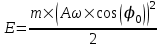 . Получим следующее: . Получим следующее: 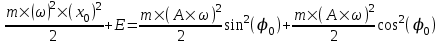 . .
Так как sin2φ+cos2φ=1, то 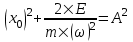 . .
Откуда амплитуда равна 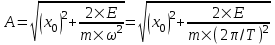 . .
Подставляем числа. 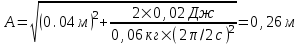 . .
Поэтому уравнение гармонических колебаний 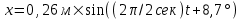 . .
Ускорение равно 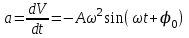 . Тогда сила равна . Тогда сила равна 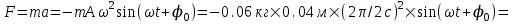
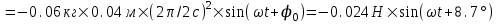 . .
|
| |
 Скачать 315.29 Kb.
Скачать 315.29 Kb.
 о определению нормальное ускорение
о определению нормальное ускорение 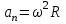 , где ω – угловая скорость точки, R - радиус. Откуда
, где ω – угловая скорость точки, R - радиус. Откуда 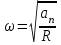 .
.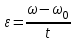 .
.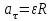 , где ε – угловое ускорение точки.
, где ε – угловое ускорение точки. 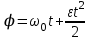 . Поэтому число оборотов равно
. Поэтому число оборотов равно 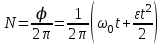 . Подставляем сюда
. Подставляем сюда 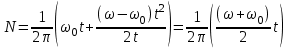 . Откуда
. Откуда 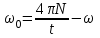 . Подставляем в
. Подставляем в 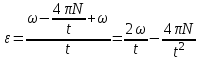 .
. 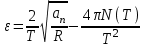 . Тогда искомая величина
. Тогда искомая величина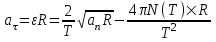 . Подставляем числа.
. Подставляем числа.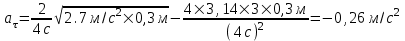 .
.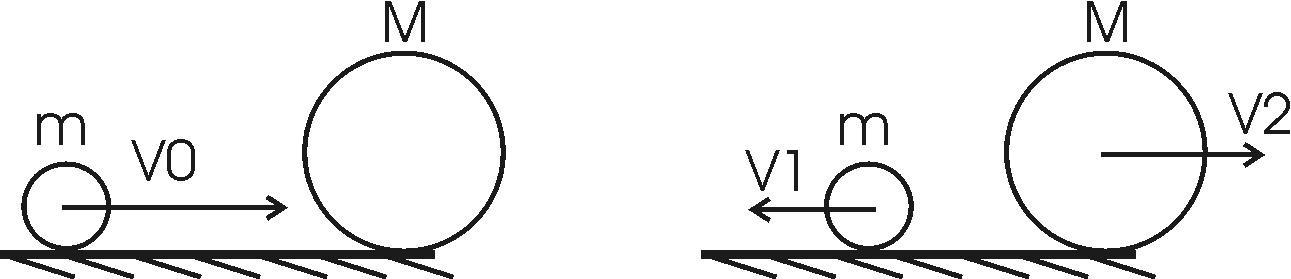
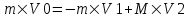 .
.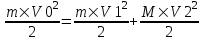 .
. 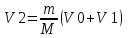 . Подставляем во второе уравнение:
. Подставляем во второе уравнение: 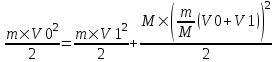 . Упрощаем:
. Упрощаем: 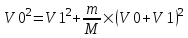 . Далее
. Далее 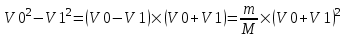 , откуда получаем
, откуда получаем 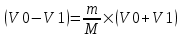 . И, наконец, находим скорость первого шара после удара:
. И, наконец, находим скорость первого шара после удара: 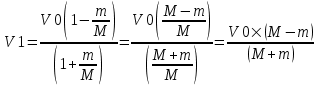 . Подставляем в
. Подставляем в 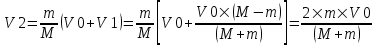 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ). 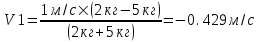 . Эта величина отрицательная, следовательно, вектор V1 должен быть направлен в противоположную сторону.
. Эта величина отрицательная, следовательно, вектор V1 должен быть направлен в противоположную сторону.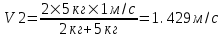 .
.
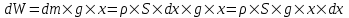 . Проинтегрируем правую и левую части:
. Проинтегрируем правую и левую части: 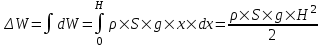 .
.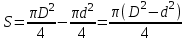 . Поэтому потенциальная энергия установки, равная совершенной работе:
. Поэтому потенциальная энергия установки, равная совершенной работе: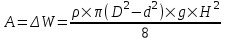 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ). 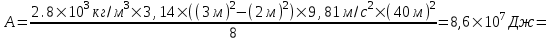

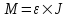 , где M – вращающий момент, ε – угловое ускорение, J – момент инерции диска. Момент инерции однородного диска массой m и диаметром D равен
, где M – вращающий момент, ε – угловое ускорение, J – момент инерции диска. Момент инерции однородного диска массой m и диаметром D равен 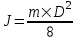 . Так как сила приложена к краю шкива, то вращающий момент этой силы равен M=F×R. Откуда угловое ускорение
. Так как сила приложена к краю шкива, то вращающий момент этой силы равен M=F×R. Откуда угловое ускорение 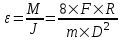 .
.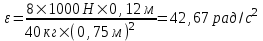 .
.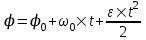 . Примем начальные условия
. Примем начальные условия 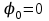 и
и 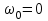 - так как начальная частота вращения равна нулю. Тогда
- так как начальная частота вращения равна нулю. Тогда 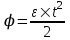 .
.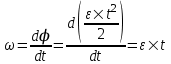 . Поэтому через время t=T угловая скорость равна
. Поэтому через время t=T угловая скорость равна 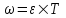 . Подставляем сюда
. Подставляем сюда 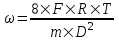 . Частота вращения равна по определению
. Частота вращения равна по определению 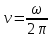 , поэтому
, поэтому 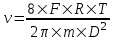
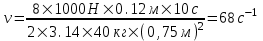 .
.
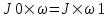 , где J0 - момент инерции диска, J – момент инерции скамьи с человеком относительно оси OO’.
, где J0 - момент инерции диска, J – момент инерции скамьи с человеком относительно оси OO’.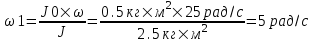 .
.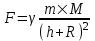 , где
, где 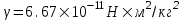 -
- 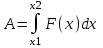 , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0),
, где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), 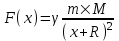 , а x – это положение (высота) тела. Тогда
, а x – это положение (высота) тела. Тогда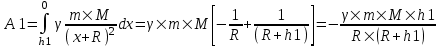 . Подставляем числа.
. Подставляем числа. 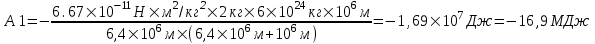 .
.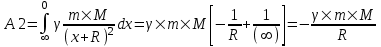 .
.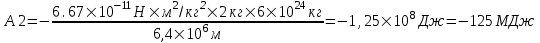 .
.
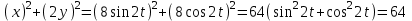 .
.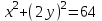 - это эллипс. По другому его записывают в виде
- это эллипс. По другому его записывают в виде 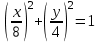 . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем:
. Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем: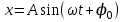 , где x –
, где x – 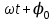 - фаза колебаний,
- фаза колебаний, 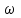 - циклическая частота, φ0 – начальная фаза.
- циклическая частота, φ0 – начальная фаза.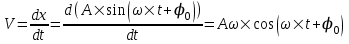 .
.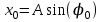 и
и 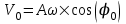 . Тогда начальная энергия равна
. Тогда начальная энергия равна 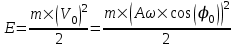 .
.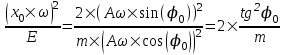 .
.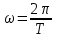 , где T – период. Поэтому
, где T – период. Поэтому 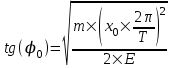 .
.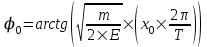 . Подставляем числа.
. Подставляем числа.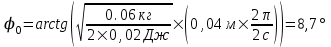
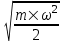 , возведем все в квадрат и сложим с
, возведем все в квадрат и сложим с 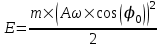 . Получим следующее:
. Получим следующее: 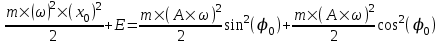 .
.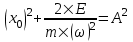 .
.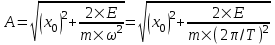 .
.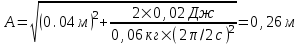 .
.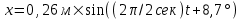 .
.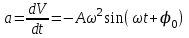 . Тогда сила равна
. Тогда сила равна 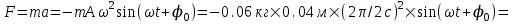
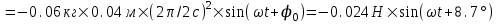 .
.