10 Основные понятия и теоремы теории вероятностей.
 Скачать 43.42 Kb. Скачать 43.42 Kb.
|
|
Тест по теме 10: «Основные понятия и теоремы теории вероятностей.» Основные понятия теория вероятностей Результат испытания называется ###. +: событием Событие, которое не может произойти в испытании, называется ###. +: невозможн#$# Вероятность невозможного события равна ###. +: 0 Вероятность случайного события больше ###. +: 0 Два события называются ###, если они могут одновременно произойти в результате одного испытания. +: совмест#$# События называются единственно ###, если хотя бы одно из них обязательно происходит в результате одного испытания. +: возможн#$# Отношение числа испытаний, в которых событие появилось, к общему числу произведённых испытаний, называют относительной ### события. +:частотой Монета брошена один раз. Вероятность того, что выпадет герб, равна: +: 0,5 Игральная кость бросается один раз. Вероятность выпадения на верхней грани более четырех очков равна… +: 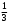 Из колоды карт (36 листов) наугад вынимается одна карта. Вероятность того, что эта карта либо дама, либо король, равна… +: 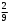 Из колоды карт (36 листов) наугад вынимается одна карта. Вероятность того, что эта карта либо туз красной масти, либо карта трефовой масти, равна… +: 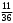 В ящике находятся 3 белых, 4 синих и 5 красных шаров. Наугад вынимают один шар. Вероятность того, что этот шар будет цветным, равна… +: 0,75 В ящике находятся 2 белых, 3 синих и 4 красных шаров. Наугад вынимают один шар. Вероятность того, что этот шар будет либо белый, либо красный, равна… +: 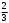 В ящике находятся 2 белых, 3 синих и 4 красных шаров. Наугад вынимают один шар. Вероятность того, что этот шар будет либо белый, либо синим, равна… +: 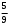 Из колоды карт (36 листов) наугад вынимается одна карта. Вероятность того, что эта карта либо туз треф, либо карта бубновой масти… +: 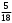 Игральная кость брошена один раз. Вероятность того, что выпадет чётное число, равна: +: 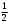 Пусть в одной коробке 5 карандашей, а в другой коробке 2 карандаша, тогда: +: можно взять один карандаш семью способами +: можно взять один карандаш из первой коробки и один из второй коробки десятью способами -: можно переложить из первой коробки во вторую карандаш тремя способами -: можно переложить из второй коробки в первую карандаш тремя способами: Игральную кость бросаем один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырех очков, равна: -: 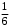 +: 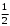 -: 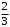 -: 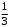 Бросаются две игральные кости один раз. Вероятность того, что сумма очков будет равна семи… +: 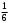 -: 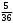 -: 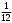 -: 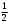 Теоремы сложения и умножения вероятностей. Их следствия. Соответствие между произвольными событиями A,B,C и их формульной записью: L1: Произошло по крайней мере (хотя бы) одно из этих событий L2: Произошло по крайней мере (хотя бы) два из этих событий L3: Произошло ровно одно из этих событий L4: Произошло ровно два из этих событий L5: Произошло не более двух событий R1: 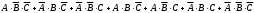 R2: 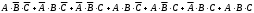 R3: 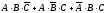 R4: 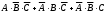 R5: 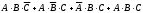 Вероятность занятости каждого из двух телефонов соответственно равны: 0,2; 0,3. Вероятность того, что оба они свободны равна: - : 0,6 - : 0,94 +: 0,56 - : 0,38 Вероятность занятости каждого из двух телефонов соответственно равны: 0,2; 0,3. Вероятность того, что только один из них свободен равна: - : 0,6 - : 0,94 - : 0,06 +: 0,38 Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,7 . Тогда вероятность того, что оба стрелка промахнутся, равна… -: 0,9 -: 0,13 -: 0,15 +: 0,12 Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,7 . Тогда вероятность того, что в цель попадёт только один стрелок, равна… -: 0,9 -: 0,18 +: 0,46 -: 0,28 В урне 3 белых и 2 черных шара. Из урны вынули два шара. Тогда вероятность того, что оба шара окажутся одного цвета, равна: -: 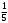 +: 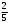 -: 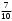 -: 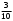 Мастер обслуживает два станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания мастера, равна 0,4, второй – 0,2. Тогда вероятность того, что в течение смены только один станок потребует внимания мастера, равна… +: 0,44 Студент разыскивает формулу в двух справочниках. Вероятность того, что нужная студенту формула есть в первом справочнике, равна 0,6, во втором - 0,8. Тогда вероятность того, что нужная формула содержится и в том и в другом справочнике, равна… +: 0,48 В ящике находятся пять изделий, из которых два бракованных. Наудачу из ящика отбирают два изделия (без возврата). Тогда вероятность того, что хотя бы одно из выбранных изделий окажется не бракованным, равна… +: 0,9 В ящике находятся пять изделий, из которых два бракованных. Наудачу из ящика отбирают два изделия (без возврата). Тогда вероятность того, что оба изделия окажутся не бракованными, равна… +: 0,3 Из колоды в 36 карт наугад одна за другой извлекаются две карты. Вероятность того, что ими оказались два туза, равна: +: 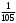 -: 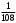 -: 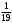 -: 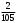 Мастер обслуживает два станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания мастера, равна 0,4, второй – 0,2. Тогда вероятность того, что в течение смены оба станка не потребуют внимания мастера, равна: +: 0,48 -: 0,52 -: 0,92 -: 0,08 Студент разыскивает формулу в двух справочниках. Вероятность того, что нужная студенту формула есть в первом справочнике, равна 0,6, во втором - 0,8. Тогда вероятность того, что нужная формула не содержится ни в одном справочнике, равна… +: 0, 08 В ящике находятся пять изделий, из которых два бракованных. Наудачу из ящика отбирают два изделия (без возврата). Тогда вероятность того, что только одно из выбранных изделий окажется не бракованным, равна… +: 0,6 Вероятность занятости каждого из трех телефонов соответственно равны: 0,7; 0,6; 0,5. Вероятность того, что хотя бы один из них свободен равна: -: 0,35 +: 0.79 -: 0.65 -: 0.21 Из колоды карт в 36 листов последовательно, с последующим возвращением в колоду извлекаются 16 карт. Наивероятнейшее число появлений карты пиковой масти равно… +: 4 -: 2 -: 7 -: 9 В первой урне 2 белых и 4 черных шара, во второй - 3 белых и 2 черных шара. Из каждой урны наудачу извлекли по одному шару. Вероятность того, что оба шара черные, равна… +: 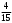 По оценкам экспертов вероятности банкротства двух банков равны 0,1 и 0,05. Тогда вероятность банкротства только одного предприятия равна… -: 0,005 +: 0,14 -: 0,05 -: 0,855 В урне 3 белых и 3 черных шара. Из урны вынули два шара. Тогда вероятность того, что оба шара окажутся белыми, равна: +: 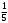 В урне 3 белых и 3 черных шара. Из урны вынули два шара. Тогда вероятность того, что оба шара окажутся разного цвета, равна: -: 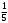 -: 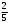 +: 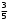 -: 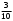 Мастер обслуживает два станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания мастера, равна 0,4, второй – 0,2. Тогда вероятность того, что в течение смены только один станок потребует внимания мастера, равна: -: 0,48 -: 0,52 +: 0,44 -: 0,08 Студент разыскивает формулу в двух справочниках. Вероятность того, что нужная студенту формула есть в первом справочнике, равна 0,6, втором - 0,8. Тогда вероятность того, что нужная формула содержится только в одном справочнике, равна… +: 0,44 В урне 3 белых и 3 черных шара. Из урны вынули два шара. Тогда вероятность того, что оба шара окажутся одного цвета, равна: -: 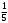 +: 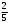 -: 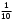 -: 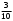 Мастер обслуживает два станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания мастера, равна 0,4, второй – 0,2. Тогда вероятность того, что в течение смены оба станка потребуют внимания мастера, равна: -: 0,48 -: 0,52 -: 0,92 +: 0,08 Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,3 . Тогда вероятность того, что в цель попадут оба стрелка, равна… +: 0,18 -: 0,9 -: 0,15 -: 0,28 В первой урне 2 белых и 4 черных шара, во второй - 3 белых и 2 черных шара. Из каждой урны наудачу извлекли по одному шару. Вероятность того, что оба шара белые, равна: -: 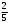 -: 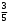 +: 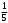 -: 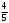 В первой урне 2 белых и 4 черных шара, во второй - 3 белых и 2 черных шара. Из каждой урны наудачу извлекли по одному шару. Вероятность того, что оба шара черные, равна: -: 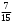 -: 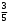 +: 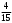 -: 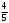 В каждой из трех урн содержится 3 белых и 6 черных шаров Из каждой урны наудачу извлекли по одному шару. Вероятность того, что все три шара белые, равна… -: 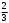 -: 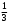 -: 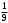 +: 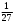 В лыжной эстафете участвуют три первокурсника и два второкурсника. Вероятность того, что первокурсник пробежит свою дистанцию быстрее нормативного времени, равна 0,4. Для второкурсника эта вероятность равна 0,5. Тогда вероятность того, что выбранный наудачу участник эстафеты, пробежит свою дистанцию не быстрее нормативного времени, равна: -: 0,20 +: 0,56 -: 0,45 -: 0,44 В лыжной эстафете участвуют три первокурсника и два второкурсника. Вероятность того, что первокурсник пробежит свою дистанцию быстрее нормативного времени, равна 0,5. Участник эстафеты закончил свой этап быстрее нормативного времени. Вероятность того, что он – второкурсник равна … +: 0,455 В телевизионном ателье имеются 4 кинескопа. Вероятность того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0.8; 0.85; 0.9; 0.95. Вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы равна... -: 0.025 +: 0.875 -: 0.925 -: 0.715 В урне 1 белый и 2 черных шара. Вероятность того, что из двух вынутых шаров (Вынутый шар в урну не возвращается) второй шар черный, равна… +: 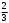 -: 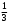 -: 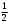 -: 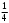 |
