ответы на экзамен с 10 по 20. 10. Вычисление и построение главного вектора и главного момента

• Название: 10. Вычисление и построение главного вектора и главного момента
• Анкор: ответы на экзамен с 10 по 20
• Дата: 25.01.2023
• Размер: 0.65 Mb.
• Имя файла: TERMEKh_OTVETY_s_10_po_20.docx
• Тип: Документы; #905499
• страница: 3 из 4

12. Приведение плоской системы параллельных сил к центру

Т 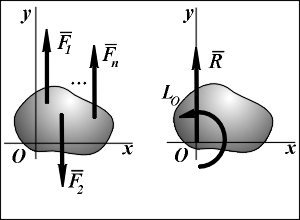еорема о приведении системы сил:

Любая система сил, действующих на абсолютно твердое тело, может быть заменена одной силой R, равной главному вектору этой системы сил и приложенной к произвольно выбранному центру О, и одной парой сил с моментом L_O, равным главному моменту системы сил относительно центра О.

Такая эквивалентная замена данной системы сил силой R и парой сил с моментом L_O называютприведением системы сил к центу О.

Рассмотрим приведение плоской системы параллельных сил к центру О, лежащему в той же плоскости (одну из координатных осей, например, ось Oy, целесообразно направить вдоль направления действия сил). В этом случае система сил заменяется одной силой и одной парой сил, лежащих в плоскости действия сил системы. Момент этой пары сил можно рассматривать как алгебраическую величину L_O и изображать на рисунках дуговой стрелкой ( алгебраический главный момент плоской системы сил ).

В результате приведения плоской системы параллельных сил к центру возможны следующие случаи:

1. 
   если R = 0, L_O = 0, то заданная система является равновесной;
   
2. 
   если хотя бы одна из величин R или L_O не равна нулю, то система сил не находится в равновесии. 
   При этом:
   
   • 
     Eсли R = 0 и L_O   0, то сис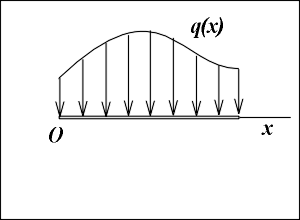тема сил приводится к одной паре сил с моментом L_O, причем в этом случае величина момента L_Oне зависит от выбора центра О.
     
   • 
     Eсли R   0, то при любом значении L_O система сил приводится к равнодействующей силе, линия действия которой параллельна линиям действия сил системы.
     

В практических задачах статики часто встречаются плоские системы параллельных сил, распределенных по некоторому закону вдоль отрезка прямой (например, вдоль прямолинейного стержня).

Плоская система распределенных сил характеризуется ее интенсивностью q, равной величине силы, приходящейся на единицу длины нагруженного отрезка. В общем случае интенсивность является некоторой функцией q(x) координаты x, отсчитываемой вдоль нагруженного отрезка.

Интенсивность измеряется в системе единиц СИ в ньютонах, деленных на метры (Н · м).

Центр параллельных сил

Рассмотрим систему параллельных сил  {F₁, F₂, ..., F_n}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а).
Эта точка называется центром параллельных сил. 
Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).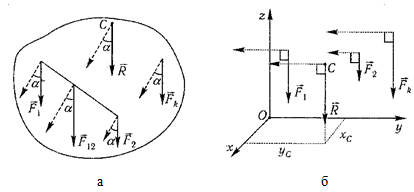


Рисунок 1.5
Для определения координат центра параллельных сил воспользуемся этой теоремой.
Относительно оси x 

 M_x(R) = ΣM_x(F_k),     _- y_CR = Σy_kFk        и        y_C = Σy_kFk /Σ_Fk.

Относительно оси y 

 M_y(R) = ΣM_y(F_k),       _- x_CR = Σx_kFk        и       x_C = Σx_kFk /Σ_Fk.

Чтобы определить координату  z_C, повернем все силы на 90° так, чтобы они стали параллельны оси  y (рисунок 1.5, б). Тогда
 M_z(R) = ΣM_z(F_k),        _- z_CR = Σz_kFk        и       z_C = Σz_kFk /Σ_Fk.

Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
 r_C = Σr_kFk /Σ_Fk.
Свойства центра параллельных сил:
1 Сумма моментов всех сил  _Fk  относительно точки  C  равна нулю   ΣM_C(F_k) = 0.

2 Если все силы повернуть на некоторый угол  α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой  C.

13. Центр тяжести твердого тела; центр тяжести объема, площади и линии. Способы определения положения центров тяжести тел.

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки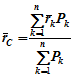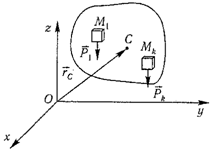




Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела  γ, вес элементарной частицы тела 

P_k = γΔV_k  (P ₌ γV) подставить в формулу для определения  r_C, имеем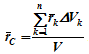



Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема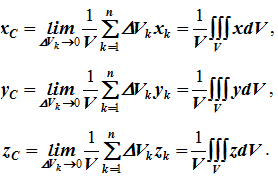



Аналогично для координат центра тяжести однородной поверхности площадью S  (рисунок 1.7, а)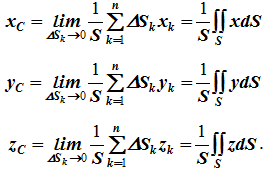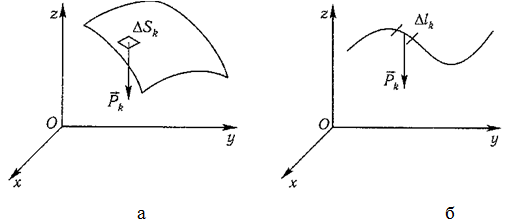





Рисунок 1.7
Для координат центра тяжести однородной линии длиной L  (рисунок 1.7, б)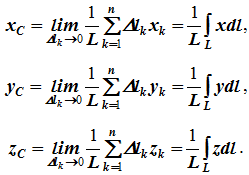




Способы определения координат центра тяжести

Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

1 Аналитический (путем интегрирования).

2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3 Экспериментальный (метод подвешивания тела).

4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C  и площадь  S известны. Например, проекцию тела на плоскость xOy  (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S₁  и  S₂ (S = S₁+ S₂). Центры тяжести этих фигур находятся в точках  C₁(x₁, y₁) и  C₂(x₂, y₂). Тогда координаты центра тяжести тела равны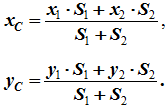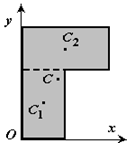





Рисунок 1.8

5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):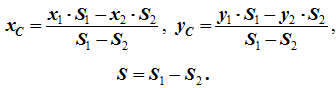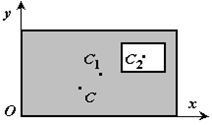





Рисунок 1.9

Центры тяжести простейших фигур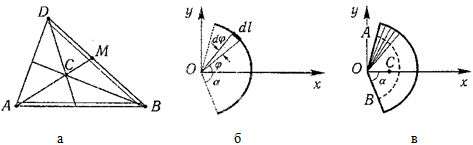

Рисунок 1.10

1 Треугольник

Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).

 DM = MB,  CM =(1/3)AM.

2 Дуга окружности

Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е.  y_C= 0.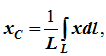



dl  – элемент дуги,  dl = Rdφ,  R – радиус окружности,  x = Rcosφ,  L =2αR,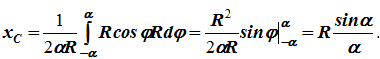



Следовательно:

 x_C= R(sinα/α).

3 Круговой сектор

Сектор радиуса  R с центральным углом  2α имеет ось симметрии  Ox, на которой находится центр тяжести (рисунок 1.10, в). 

Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса  (2/3)R. 

Центр тяжести сектора совпадает с центром тяжести дуги  AB: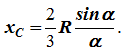



14. Способы задания движения точки.

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета. 



При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них  t.
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.

15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени  Δt:



тогда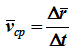 


средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени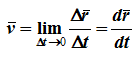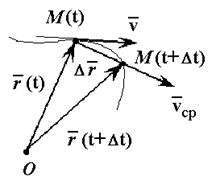




Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.

1.3 Ускорение точки
Среднее ускорение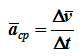  



характеризует изменение вектора скорости за малый промежуток времени  Δt . Ускорение точки в данный момент времени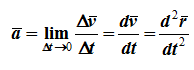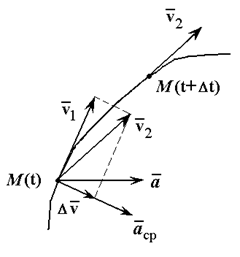



Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

15. Определение скорости и ускорения при координатном способе задания движения точки.
Связь векторного способа задания движения и координатного дается соотношением


Из определения скорости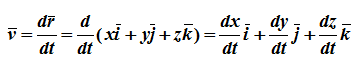


Проекции скорости на оси координат равны производным соответствующих координат по времени: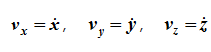


Модуль и направление скорости определяются выражениями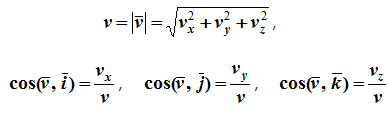


Из определения ускорения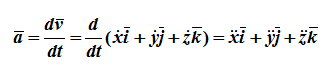



Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени


Модуль и направление ускорения определяются выражениями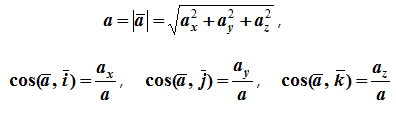



16. Тангенциальное и нормальное ускорение точки.

Нормальное и тангенциальное ускорение