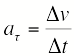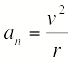ответы на экзамен с 10 по 20. 10. Вычисление и построение главного вектора и главного момента
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
| |
| При криволинейном движении скорость направлена по касательной к траектории. 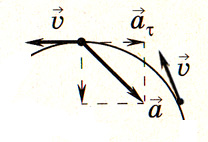 Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным | |
| В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением | |
| |
| Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением | |
| |
| Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения | |
|
17. Относительное, переносное и абсолютное движения. Теорема о сложении скоростей.
Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)
aa = ar ⊕ ae ⊕ aC .
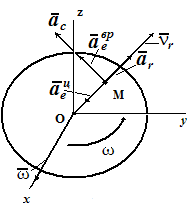
Рис. 3
Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение ar направлено вдоль этой прямой и определяется выражением
Переносным ускорением точки M является ускорение точки Mдиска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением
ae= aeвр⊕ aeцс ,
где aeвр= ε⋅ OM - вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;
aeцс= ω2⋅ OM - центростремительное ускорение точки M, направленное к центру диска.
Ускорение Кориолиса или поворотное ускорение определяется по формуле
aC = 2 ωe ⊗ νr, где ωe - переносная угловая скорость, νr - относительная скорость точки.
Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.
Величина ускорения Кориолиса определяется выражением
aC = 2 ωe νr sinα ,
где α – угол между векторами ωe и νr.
Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка Mдвижется относительно диска с постоянной относительной скоростью (рис.4).
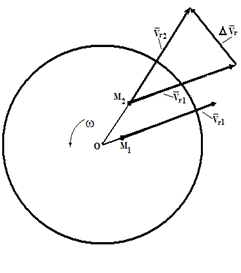
Рис. 4
Пусть в момент времени t1 точка M занимала положение M1 и имела относительную скорость νr 1 . За промежуток времени Δt точка M переместится в положение M2 , при этом направление скорости νr изменится вследствие вращения диска. Векторνr получит приращение Δνr . Отношение Δνr/ Δt определяет среднее ускорение точки за промежуток времени Δt . Предел отношения Δνr/ Δt при Δt→ 0 есть производная dνr/dt , как производная от вектора постоянного по величине.
Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t1 и t2 переносная скорость определяется выражениями νe1= ω⊗ OM1и νe2= ω⊗ OM2 . Тогда приращение вектора νe за счет относительного движения будет равно
Δνe = ω ⊗ OM2 - ω ⊗ OM1 = ω ⊗ (OM2 - OM1) = ω ⊗ νr⋅Δt
Отношение Δνe / Δt в пределе при Δt→ 0 дает производную dνe/ d t= ω ⊗ νr. Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.
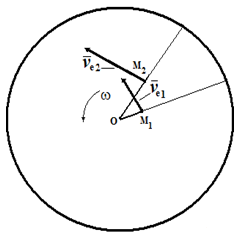
Рис. 5
Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых
Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:
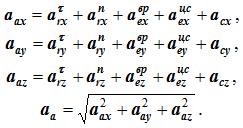
18. Поступательное движение тела.
18. Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.
Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.
Рис. 1.1
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
Доказательство.
Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением
Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точкиB – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.
Продифференцируем по времени выражение
Получаем
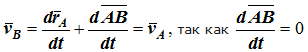
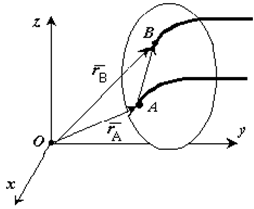
Рис. 1.2
Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.
Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

19. Вращательное движение тела. Угловая скорость и угловое ускорение.
19. Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
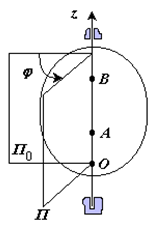
Рис. 1.3
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
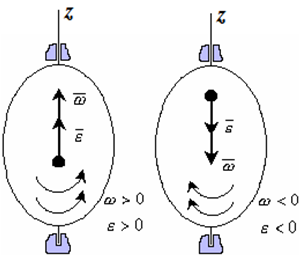
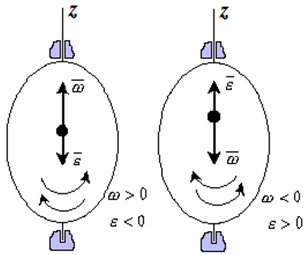
Рис. 1.4
Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.
При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .
Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.
Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторыω и ε направлены в противоположные стороны.
Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения
φ=φ0+ωt
Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращения
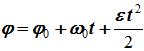
и уравнение, выражающее угловую скорость в любой момент времени
ω=ω0+εt
представляют совокупность основных формул вращательного равнопеременного движения тела.
20. Скорости и ускорения точек при вращательном движении.
Так как траектории точек вращающегося тела – окружности, при определении скорости и ускорения удобно воспользоваться естественным способом задания движения (рисунок 1.5). Дуговая координата, определяющая положение точки на траектории, связана с углом поворота равенством:
s = φR . Отсюда:
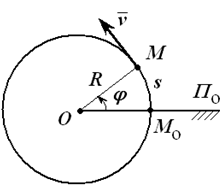
Рис. 1.5
Скорость ν = νττ еще называют линейной или окружной скоростью. Она направлена по касательной к траектории движения точки.
Ускорение (рисунок 1.6) определяется как сумма касательного и нормального ускорений:
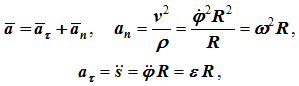
модуль ускорения
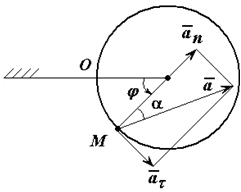
Рис. 1.6
Угол α, образованный вектором ускорения точки с радиусом окружности OM, для всех точек тела в любой момент времени одинаков,
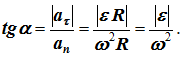
Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным:
Векторные выражения скорости и ускорения точек вращающегося тела
Модуль скорости точки вращающегося тела ν = ωR = ωr sinβ (рисунок 1.7) равен модулю векторного произведения ω⊗r.
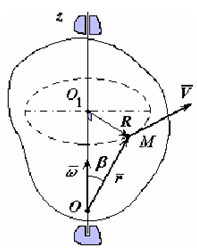
Рис. 1.7
Следовательно:
ν = ω×r(формула Эйлера).
Определим ускорение точки, продифференцировав формулу Эйлера:
Первое слагаемое является касательным ускорением aτ= ε ⊗ r,
а второе – нормальным an = ω ⊗ (ω ⊗ r) = ω ⊗ ν.