ответы на экзамен с 10 по 20. 10. Вычисление и построение главного вектора и главного момента
 Скачать 0.65 Mb.
|
|
10. Вычисление и построение главного вектора и главного момента Выбираем систему координатных осей Oxyz (рис. 48) и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:   Рис. 48. По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R (см. также рис. 26). Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами: 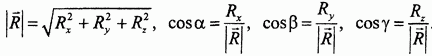 Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:  К формулам для вычисления проекций главного момента необходимо привести следующие пояснения. Главный момент, по определению, есть векторная сумма моментов всех сил  центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:  Отсюда непосредственно следуют написанные выше выражения для величин  .Косинус угла  между главным вектором и главным моментом определяется так: Формула получается следующим образом. По определению скалярного произведения векторов R и  имеем: С другой стороны, эта же величина может быть вычислена через проекции векторов-сомножителей:  Приравнивая правые части и разрешая полученное уравнение относительно coscp, приходим к написанной формуле. Условия равновесия произвольной плоской системы сил. Случай параллельных сил. Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M0 = 0. Здесь О - любая точка плоскости. Найдем вытекающие из равенств аналитические условия равновесия. Величины R и Мо определяются равенствами:  Равенства выражают, следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.  Равновесие плоской системы параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Oxбудет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия: Где ось Оу параллельна силам.  |