Лекция Термех. ЛЕКЦИЯ 5с. 5. произвольная пространственная система сил момент силы относительно центра как вектор

• Название: 5. произвольная пространственная система сил момент силы относительно центра как вектор
• Анкор: Лекция Термех
• Дата: 29.12.2022
• Размер: 387 Kb.
• Имя файла: ЛЕКЦИЯ 5с.doc
• Тип: Лекция; #868550

ЛЕКЦИЯ 5

5. ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ

СИСТЕМА СИЛ

5.1. Момент силы относительно центра как вектор

Ч 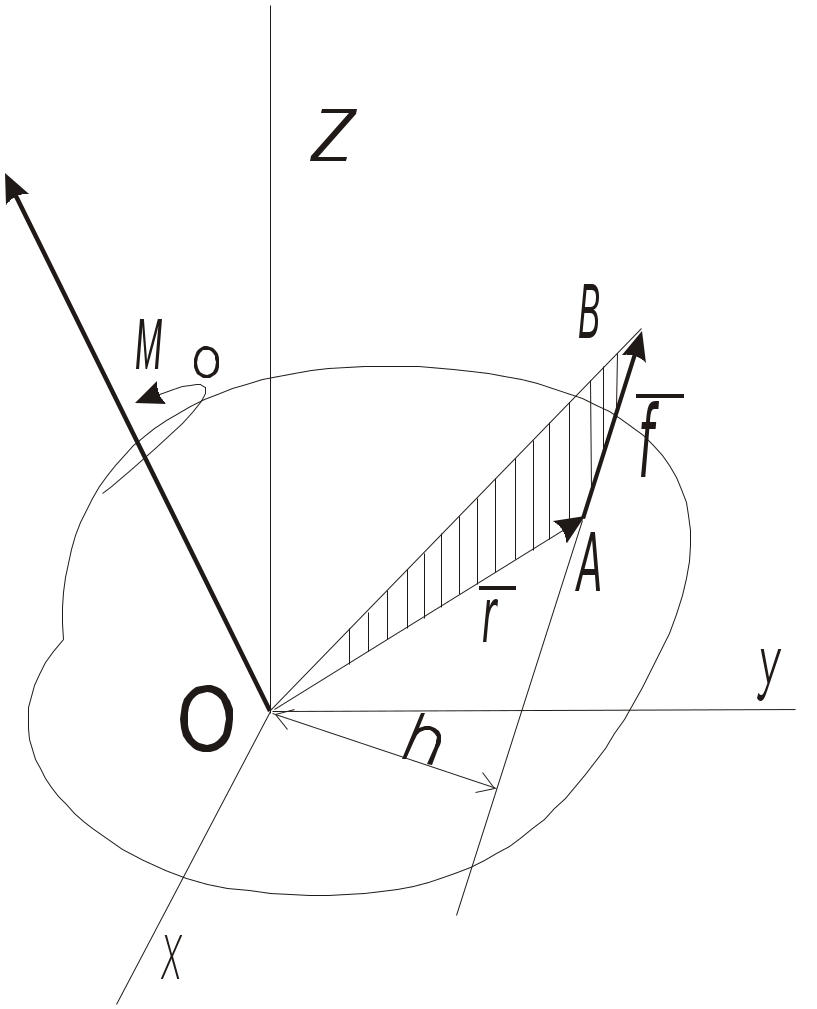тобы перейти к решению задач данного типа необходимо уточнить и расширить ряд введённых ранее понятий. Так момент силы относительно центра О как характеристика её вращательного эффекта определяется следующими параметрами

1) модулем момента, равным ;

2) плоскостью поворота ОАВ, проходящей через линию действия силы и центр О;

3)направлением поворота в этой плоскости.

Когда все силы и центр О лежат в одной плоскости, необходимость задавать плоскость АОВ отпадает и момент определяется произведением , где знак указывается направлением поворота. Но в случае произвольно расположенных сил в пространстве, плоскости поворота у разных сил будут разными и должны задаваться дополнительно.

Положение плоскости в пространстве можно задать, задав отрезок (вектор), перпендикулярный к этой плоскости. Если одновременно модуль этого вектора выбрать равным модулю момента силы и условиться направлять этот вектор так, чтобы его направление определяло направление поворота силы, то такой вектор полностью определит все три элемента, характеризующие момент данной силы относительно центра О.

И так, в общем случае: момент силы относительно центра О будем изображать приложенным в центре О вектором равным по модулю (в выбранном масштабе) произведению модуля силы на плечо и перпендикулярным к плоскости ОАВ, проходящей через центр О и силу .

Направлять вектор будем в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки.

Таким образом вектор будет одновременно характеризовать: модуль момента, плоскость поворота АОВ и направление поворота в этой плоскости. Точка приложения вектора — центр вращения.

5.2. Момент силы относительно оси

Момент силы относительно оси характеризует вращательный эффект, создаваемый силой, стремящийся повернуть тело вокруг данной оси.

Р 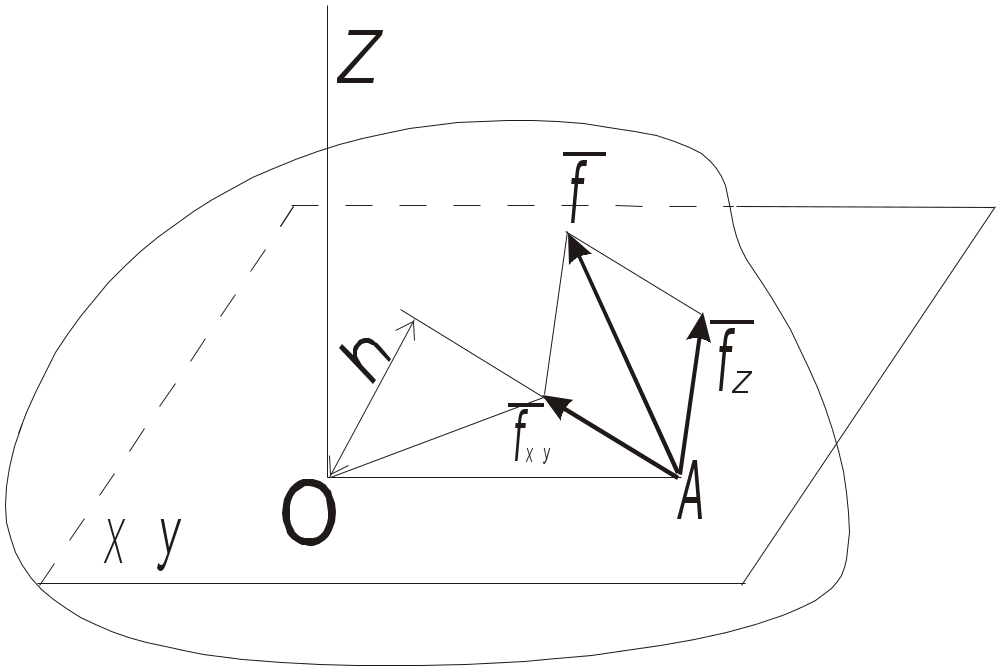ассмотрим твёрдое тело, которое может вращаться вокруг некоторой оси Z, пусть на это тело действует сила , приложенная в точке А. Проведём через точку А плоскость xy  oZ и разложим силу на составляющие: и , лежащую в плоскости xy( является одновременно и проекцией силы на плоскость xy).

Проекция не может повернуть тело вокруг этой оси, она стремиться сдвинуть тело вдоль оси Z. Следовательно, весь вращательный эффект создаёт проекция , отсюда

.
Для силы же вращательный эффект измеряется произведением модуля силы на расстояние h до оси. Но этой же величиной измеряется момент силы относительно точки О, в которой ось Z пресекает плоскость xy. Следовательно
;
т.е. моментом силы относительно оси называется скалярная величина равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.

М 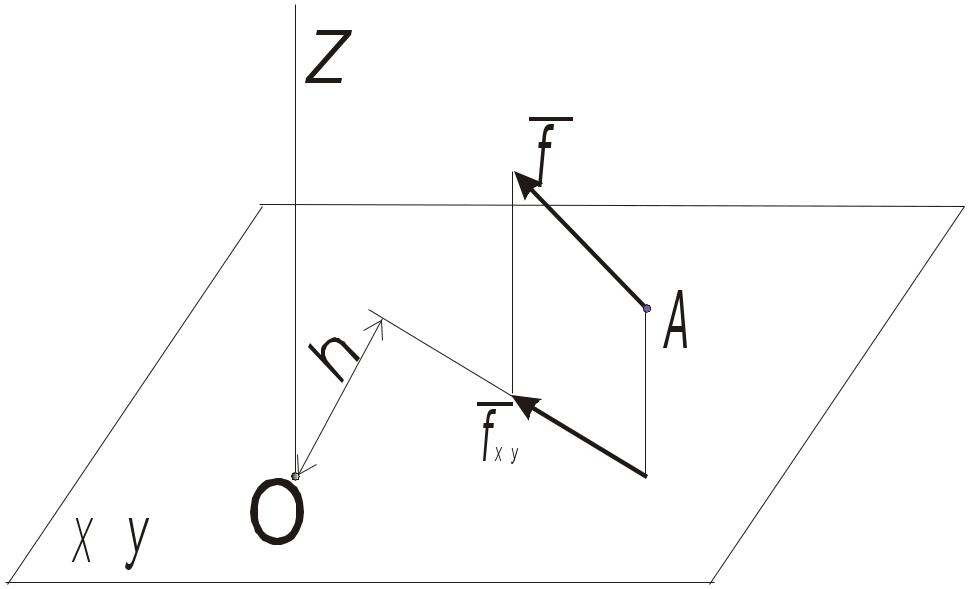омент считаем со знаком плюс, если с положительного конца оси Z поворот, который сила стремиться совершить, виден происходящим против хода часовой стрелки, и отрицательным – если наоборот.

Из чертежа видно, что плоскость xy можно проводить через любую очку оси Z.

Отсюда, для нахождения момента необходимо:

1. Провести плоскость xy, перпендикулярную оси Z;

2. Спроектировать силу на эту плоскость и вычислить величину ;

3. Опустить из точки О перпендикуляр на направление и найти длину плеча h;

4. Вычислить величину ;

5. Определить знак момента.

Частные случаи:

1. 
   Если сила параллельна оси, то , так как ;
   
2. 
   Если линия действия силы пересекает ось, то , так как .
   

5.3. Момент пары сил как вектор

Действие пары сил на твёрдое тело характеризуется: модулем момента пары, плоскостью действия, направлением поворота в этой плоскости.

Если пары не лежат в одной плоскости, то для характеристики необходимо задать все три вектора параметра. Это можно сделать если, аналогично моменту силы, изображать момент пары, вектором, т.е. будем изображать момент пары вектором или , модуль которого равен (в выбранном масштабе) модулю момента пары, т.е. произведению одной из её сил на плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки.

Так как пару можно располагать где угодно в плоскости её действия (или параллельной плоскости) то вектор можно прикладывать в любой точке тела (такой вектор называется свободным).

Легко видеть, что вектор определяет данную пару в полной мере. Зная и проведя любую плоскость , найдём плоскость действия пары; измерив длину , определим модуль момента пары; а по направлению установим направление поворота пары.

5.4. Сложение пар в пространстве

Теорема: любая система пар, действующая на абсолютно твёрдое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар.

Доказательство теоремы аналогично доказательству сложения пар на плоскости, только все пары раскладываются на силы, плечом которых является линия пресечения плоскостей.

Откуда получаем:

.
Если слагаемые векторы не лежат в одной плоскости, то подсчёт удобнее вести аналитически, используя теорему о проекциях суммы векторов на ось, т.е.

; ; ;

где

.
Отсюда условия равновесия системы пар, действующих на твёрдое тело

, ;

или

= 0; = 0; = 0.
Если векторы моментов лежат в одной плоскости, то их сложение сводится к алгебраической сумме.

5.5. Приведение пространственной системы сил

к данному центру

Эта задача решается с помощью теоремы о параллельном переносе силы. Рассмотрим твёрдое тело, на которое действует какая угодно система сил , ,…, .

В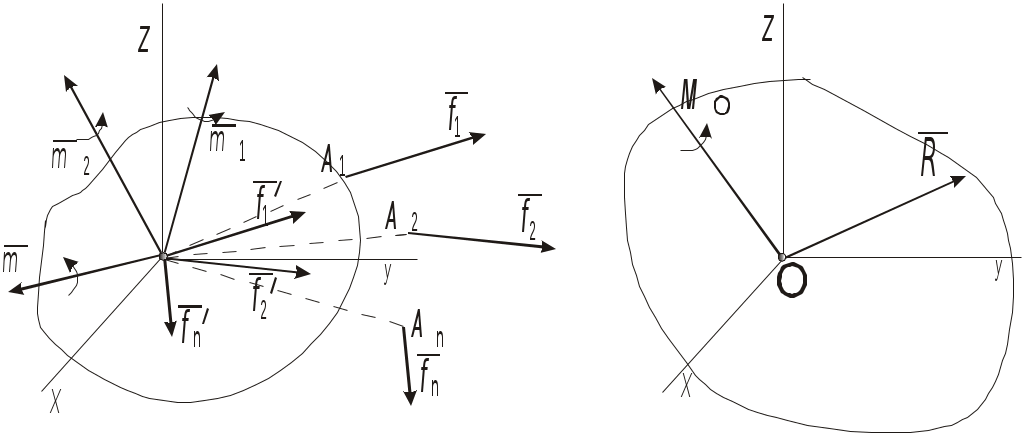
ыберем произвольную точку О за центр приведения и перенесём все силы системы в этот центр, присоединяя при этом соответствующие пары.


Тогда на тело будет действовать система сил , , …, , приложенных в центре О, и система пар, моменты которых будут равны:
, , …, .
Силы приложенные в точке О заменяются одной силой , приложенной в той же точке

.
Система пар заменяется одной парой, момент которой равен

,
как и в случае плоской системы величина называется главным вектором системы; величина – главным моментом системы относительно этого центра.

Векторы и обычно определяются аналитически, т.е. по их проекциям на оси координат
, , ;
; ;
.

5.6. Условия равновесия

произвольной пространственной системы сил

Так как произвольную пространственною систему сил можно привести к какому-нибудь центру О и заменить одной результирующей силой и парой с моментом , то для равновесия этой системы сил необходимо и достаточно, чтобы одновременно было и . Но эти векторы могут быть равны нулю тогда, когда их проекции на оси координат равны нулю, т.е.

и ;
или когда действующие силы удовлетворяют условиям:
= 0, = 0, = 0;
= 0, = 0, = 0.
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх координатных осей и суммы их моментов относительно этих осей были равны нулю.

Первые три уравнения – отсутствие перемещения вдоль трех координатных осей, а последние три – отсутствие вращения вокруг них.

Для системы параллельных сил:
= 0; = 0, = 0.
остальные равенства обращаются в тождества.

5.7. Теорема Вариньона

о моменте равнодействующей относительно оси

Теорема: Если данная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов слагаемых сил относительно той же оси.

При решении задач на равновесие произвольной пространственной системы сил сохраняется тот же порядок, что и для произвольной плоской системы сил.
Вопросы для самоконтроля

1. 
   Как привести силу к заданному центру?
   
2. 
   Теорема о приведении произвольной системы сил к простейшему виду (теорема Пуансо).
   
3. 
   Что такое главный вектор?
   
4. 
   Что такое главный момент?
   
5. 
   Как определить модуль главного вектора и главного момента?
   
6. 
   Зависит ли главный момент от выбора центра приведения?
   
7. 
   К какому простейшему виду можно привести произвольную пространственную систему сил, если:
   

а) главный вектор равен нулю, а главный момент не равен нулю;

б) главный вектор не равен нулю, а главный момент равен нулю;

8. 
   Теорема Вариньона о моменте равнодействующей.
   
9. 
   Векторные и аналитические условия равновесия произвольной пространственной системы сил.
   
10. 
    Сколько и каких уравнений равновесия можно составить для пространственной системы параллельных сил?