Заказ 34151. Сопромат. Решение. Решение Дано Определим величину внешнего скручивающего момента
 Скачать 232.74 Kb.
|
|
Задача N 1. Для стержня, загруженного пятью моментами, из которых один имеет неизвестную величину, определить крутящие моменты в сечениях и построить эпюру крутящего момента T. Решение Дано:      1.Определим величину внешнего скручивающего момента  :  2.Построим эпюру крутящих моментов. Для этого разделим вал на участки. Границей участка будет являться точка приложения внешнего скручивающего момента. Определим крутящие моменты в сечениях. Участок I. Запишем уравнение равновесия для первого участка:   Участок II. Запишем уравнение равновесия для второго участка:   Участок III. Запишем уравнение равновесия для третьего участка:   Участок IV. Запишем уравнение равновесия для четвертого участка:   Построим эпюру крутящих моментов по полученным значениям:  Задача N 2. Для стержня переменного сечения, загруженного сосредоточенными силами, определить продольные усилия с учетом собственного веса и построить эпюру продольной силы  . Объемный вес материала стержня . Решение Дано:         Определяем продольные усилия на всех участках стержня с учетом собственного веса. Сечение I-I на участке 1-2.  Сечение II-II на участке 2-3.  Сечение III-III на участке 3-4.  На основе полученных выражений строим эпюру продольных усилий  .Сечение 1-1 на участке 1-2.  Сечение 2-2 на участке 1-2.  Сечение 2-2 на участке 2-3.   Сечение 3-3 на участке 2-3.   Сечение 4-4 на участке 3-4.    . Задача N 3. Определить усилия в различных балках при поперечном изгибе и построить эпюры поперечной силы  и изгибающего момента  .Решение Дано:        Вычисляем опорные реакции:       Из (2) следует:  Подставляя в (4) числовые значения получим:  Из (3) следует:  Подставляя в (5) числовые значения получим:  Подставляем полученные значения реакций опор в уравнение (1) и выполняем проверку:  Составим аналитические выражения изменения изгибающего момента  .Участок I.   Так как ветви параболы направлены вниз найдем ее максимальное значение. Для этого продифференцируем выражение для момента и приравняем производную к нулю.  Отсюда находим  : Подставив, полученное значение в уравнение для момента получим его максимальное значение на участке:  Участок II.     Участок III. 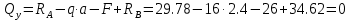    Строим эпюры изгибающих моментов  и поперечных сил  .Участок I.  Точка    Точка     Участок II.  Точка   Точка   Участок III.     Задача N 4. Задание то же что и в задаче 3. Решение Дано:       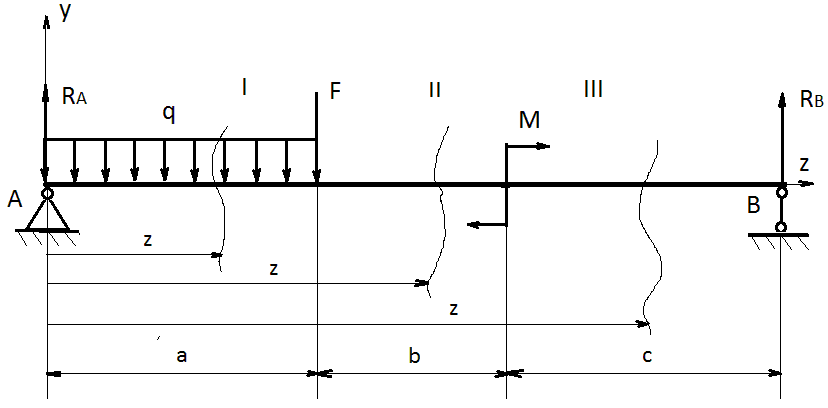 Вычисляем опорные реакции:   Из выражения (2) следует:  Подставляя в (4) числовые значения получим:  Из выражения (3) следует:  Подставляя в (5) числовые значения получим:  Подставляем полученные значения реакций опор в уравнение (1) и выполняем проверку:  Составим аналитические выражения изменения изгибающего момента .Участок I.   Так как ветви параболы направлены вниз найдем ее максимальное значение. Для этого продифференцируем выражение для момента и приравняем производную к нулю.  Отсюда находим : максимальное значение находится вне пределов участка. Участок II.    Участок III.    Строим эпюры изгибающих моментов и поперечных сил .Участок I.  Точка   Точка    Участок II.  Точка   Точка   Участок III. 2  Точка  Точка   Задача N 5. Задание то же что и в задаче 3. Решение Дано:        Вычисляем реакции заделки:   Из (1) следует:  Подставляя в (3) числовые значения получим:  Из (2) следует:  Подставляя в (4) числовые значения получим:  Составим аналитические выражения изменения изгибающего момента .Участок I   Так как ветви параболы направлены вниз найдем ее максимальное значение. Для этого продифференцируем выражение для момента и приравняем производную к нулю.  Отсюда находим : максимальное значение находится вне пределов участка. Участок II     Строим эпюры изгибающих моментов и поперечных сил .Участок I  Точка    Точка    Участок II  Точка   Точка    |