теория вероятностей задача. 11 вопрос тервер. 11. Дисперсия и ее свойства (без доказательства). Среднее квадратическое отклонение
 Скачать 15.06 Kb. Скачать 15.06 Kb.
|
|
11. Дисперсия и ее свойства (без доказательства). Среднее квадратическое отклонение. Определение. Дисперсией случайной величины ξ называется число Dξ = M(ξ – m)2 , где m – математическое ожидание ξ. Другая формулировка: Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = M[X – M(X)]2. Свойство 1. Если случайная величина ξ является постоянной, то Dξ = 0. Свойство 2. Добавление постоянной к случайной величине не меняет ее дисперсии, т. е. D(ξ + C) = Dξ. Свойство 3. Постоянный множитель выносится за знак дисперсии в квадрате, т. е. D(Cξ) = С2 Dξ. Свойство 4. Дисперсия произвольной случайной величины неотрицательна, причем она равна нулю тогда и только тогда, когда случайная величина ξ является постоянной с вероятностью 1. Свойство 5. Для произвольной случайной величины ξ Dξ = М(ξ2) – (Мξ)2. Дисперсия имеет размерность квадрата случайной величины. Это лишает наглядности дисперсию как числовую характеристику. Поэтому для характеристики разброса значений случайной величины используют среднее квадратическое отклонение, которое равно положительному значению корня квадратного из дисперсии: {\displaystyle \sigma } σ(Х) = 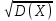 . . |
