идз физика. 11 Дж. Определить амплитуды напряженностей электрического и магнитного полей. Считать

• Название: 11 Дж. Определить амплитуды напряженностей электрического и магнитного полей. Считать
• Дата: 27.11.2022
• Размер: 0.87 Mb.
• Имя файла: идз физика.doc
• Тип: Документы; #814505

1. Энергия, переносимая плоской электромагнитной волной в вакууме за время 1 мин через площадку 10 см², расположенную перпендикулярно к направлению распространения волны, составляет 8,0·10^-11 Дж. Определить амплитуды напряженностей электрического и магнитного полей. Считать T << t, где T – период волны.

Дано:









Найти:





Решение

Энергия переносимая электромагнитной волной за единицу времени через единицу поверхности, перпендикулярной направлению распространения волны, определяется вектором Пойнтинга:

(1)

Где – вектор плотности потока электромагнитной энергии;   – вектор напряженности электрического поля; – вектор напряженности магнитного поля.



Учитывая, что в электромагнитной волне векторы и  взаимно перпендикулярны и перпендикулярны направлению распространения волны, получим для модуля вектора выражение:

(2)

Поскольку обе величины E, H, характеризующие электромагнитную волну, в каждой ее точке меняются во времени по закону синуса, находясь в одинаковых фазах, соотношение (2) можно записать так:

(3)

Где и соответственно амплитудное значение напряженности электрического и магнитного поля; – циклическая частота; – время.

Согласно определению вектора плотности потока энергии, можем записать:



Отсюда энергия , переносимая волной через площадку за время равна:

(4)

Подставим (3) в (4):

(5)

Согласно теории электромагнитных волн, плотности энергии электрического и магнитного полей волны в любой момент времени равны, т.е.

(6)

где Ф/м – электрическая постоянная;   – диэлектрическая проницаемость среды (в нашем случае );, – магнитная проницаемость среды (в нашем случае ); – магнитная постоянная.

Из (6) можем записать:

(7)

Так же связаны между собой и амплитудные значения , . Тогда уравнение (7) можем записать так:

(8)

Подставим (8) в (5):

(9)

Отсюда:

(10)

Произведем замену и разобьем интеграл на два:



Согласно условию задачи, , тогда членом можно пренебречь. Тогда последнее выражение примет вид:



Отсюда:

(11)

Подставим (11) в (8):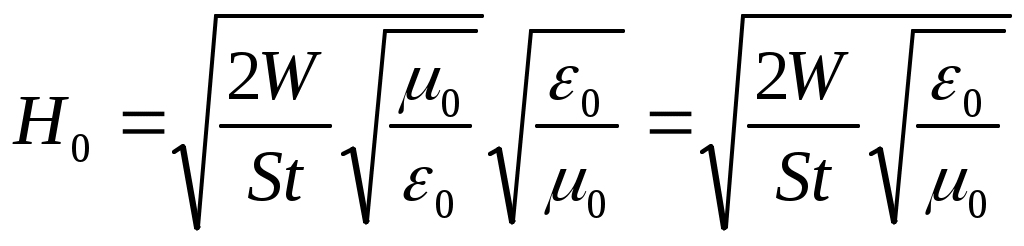



(12)

Проверим размерность формулы (11):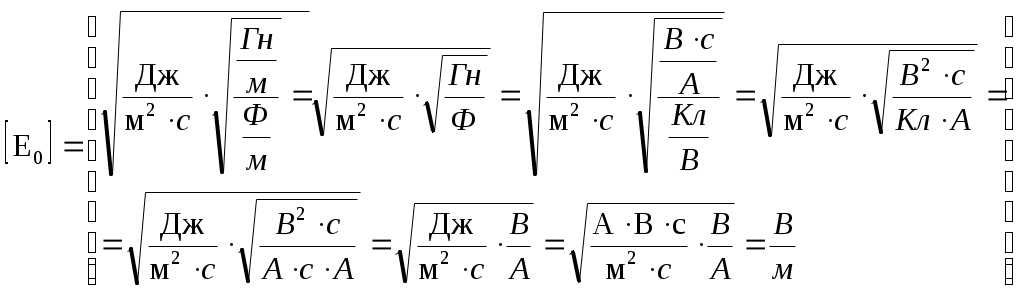



Проверим размерность формулы (12):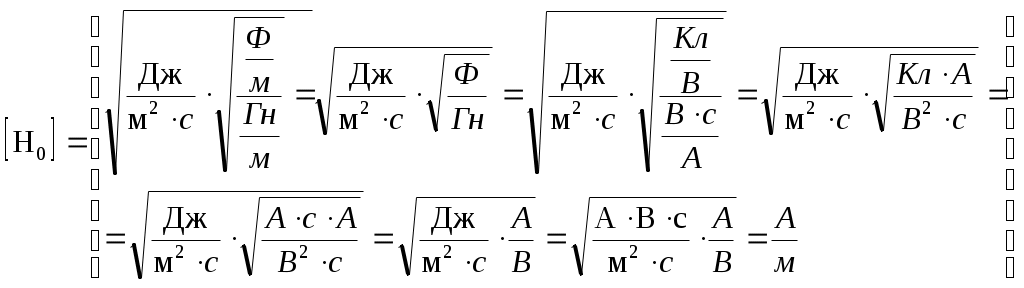


Подставим данные в (11):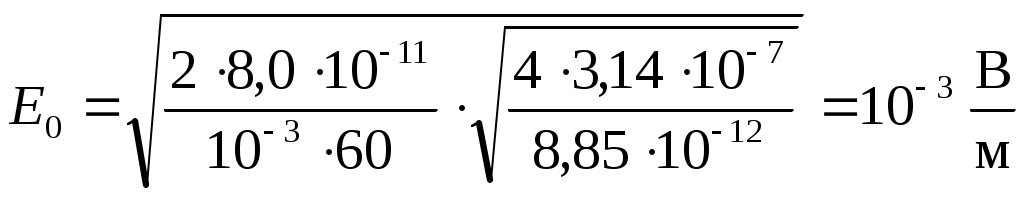



Подставим данные в (12):



Ответ: ;

2. В цепь переменного тока напряжением 220 В включены последовательно емкость, активное сопротивление 10 Ом и индуктивность. Найти ток, проходящий через контур, если известно, что падение напряжения на конденсаторе U_C = 2U_R и падение напряжения на индуктивности U_L = 3U_R.

Дано:



_R=10 Ом

U_C = 2U_R

U_L = 3U_R

Найти:

I – ?

Решение



Построим векторную диаграмму, учитывая, что напряжение в резистивном элементе 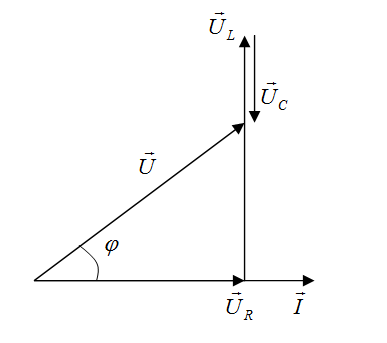совпадает по фазе с током в цепи, напряжение в индуктивном элементе опережает по фазе ток на угол , а напряжение в емкостном элементе отстает по фазе от тока на угол .



Из рисунка можем записать:



Подставим данные:



Отсюда:



Тогда ток равен: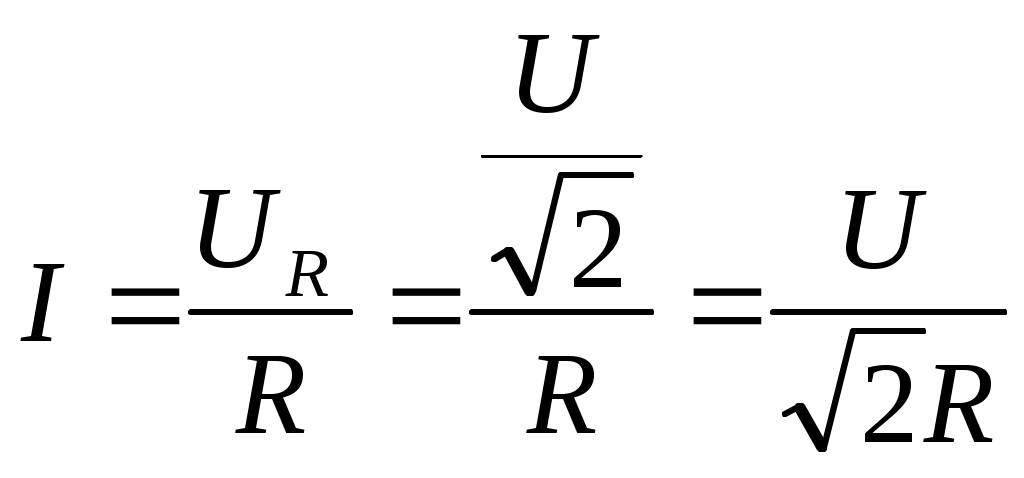





Проверим размерность:





Ответ: .
3. Определить расстояние между центром интерференционной картины и пятой светлой полосой в установке с зеркалами Френеля, если угол между зеркалами 20^/. Расстояние от зеркал до источника и экрана равны соответственно 20 см и 2 м. Длина волны 540 нм.

Дано:











Найти:



Решение



При отражении света от двух зеркал на экран падают два световых пучка. Так как эти пучки идут от одного и того же источника, то они когерентны и, перекрываясь, дают на экране интерференционную картину. Мнимые изображения источника в зеркалах играют роль когерентных источников и .

Найдем ширину интерференционной полосы на экране. Для этого рассмотрим следующий рисунок.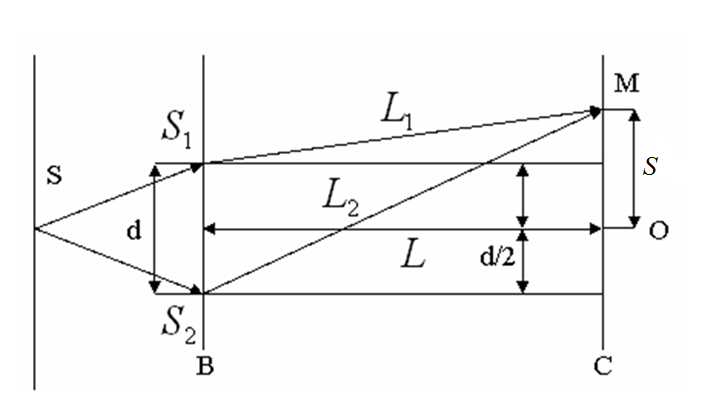



В некоторой точке М экрана С будет наблюдаться интерференционный максимум при выполнении условия

(1)

где   – оптическая разность хода; целое число k называется порядком интерференционного максимума: . ; – длина волны.

Так как показатель преломления воздуха n = 1, то оптическая разность хода равна:

   (2)

Где – расстояние от второй щели до точки М; – расстояние от первой щели до точки М.

Обозначим через расстояние от точки М до точки О, симметричной относительно щелей. Из рисунка видно, что:

(3)

(4)

С формул (3) и (4) можем записать:



Или

(5)

Из условия L >> d следует, что , поэтому уравнение (5) запишем так:
(6)

Подставим (2) в (6):

(7)

Отсюда:

(8)

Подставим (1) в (8):

(9)

За формулой (9) можно найти координату -го максимума. Тогда При найдем ширину интерференционной полосы . Тогда последнее выражение запишем так:

(10)

где L – расстояние от источников до экрана; d – расстояние между когерентными источниками.

Чтобы найти расстояние от центра интерференционной картины до точки, в которой кончается пятая светлая полоса, необходимо её ширину умножить на , т.е.:

(11)

Расстояние от источников до экрана, как видно из первого рисунка, равно:

, где , , следовательно, можем записать, что:

(12)

Где – расстояние от зеркал до экрана .

Из рисунка можем записать, что расстояние между когерентными источниками равно:

(13)

Подставив (12) и (13) в (11), получим:



Поскольку угол мал, то можем записать, что , . Учитывая это, последнее выражение примет вид:



_{Проверим размерность:}



Подставим данные:



Ответ:

4. Найти радиус первого темного кольца Ньютона, если между линзой и пластинкой налит бензол (n = 1,5). Радиус кривизны линзы 1 м. Показатели преломления линзы и пластинки одинаковы. Наблюдение ведется в отраженном свете ( = 589 нм).

Дано:









Найти:

– ?

Решение


Появление колец Ньютона обусловлено интерференцией световых пучков, отраженных от двух поверхностей тонкой воздушной прослойки между линзой и пластинкой. Оптическая разность хода лучей равна:

(1)

Где – абсолютный показатель преломления бензола, налитого между линзой и пластинкой. Слагаемое учитывает, что при отражении пучка от оптически более плотной среды (считаем, что линза и пластина стеклянные с показателем преломления 1,65) фаза колебаний изменяется на противоположную.

Из прямоугольного треугольника АВО можем записать:

(2)

Где – радиус линзы; – радиус кольца Ньютона.

Поскольку, , то можем записать:



Тогда выражение (2) перепишем так:



Отсюда:

(3)

Запишем условие интерференционного минимума:

(4)

Где – порядок интерференционного минимума.

Из выражений (2) и (5) можем записать:




Отсюда:

(5)

Из выражений (3) и (5) можем записать:



Отсюда:



Проверим размерность:



Подставим данные, учитывая, что для первого темного кольца , :



Ответ: .
5. Вычислить радиус первой зоны Френеля, если расстояние от источника света до зонной пластинки равно 445 см, а расстояние от пластинки до экрана равно 190 см и длина волны 455 нм.

Дано:









Найти:



Решение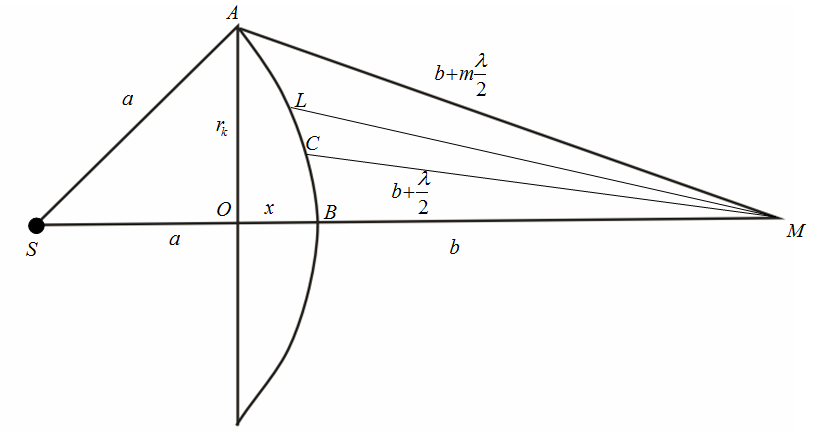



От точечного источника S распространяется сферическая волна, волновая поверхность которой - сфера. Дойдя до края диска (точка А), волны дифрагируют, то есть отклоняются от первоначального направления распространения. В соответствии с принципом Гюйгенса-Френеля каждая точка, до которой дошла волна, становится источником вторичных волн, распространяющихся во все стороны. Огибающая фронтов вторичных волн представляет новый фронт волны. Причем все вторичные волны когерентны, то есть могут в точке схождения интерферировать. Поэтому при определенных условиях в точке М можно наблюдать интерференционную картину, получившуюся в результате дифракции волн.

1. 
   Проведем из точки М конические поверхности до пересечения с волновой поверхностью АВ сферической волны. Длина образующей конической поверхности равна  , длина  и т.д. На волновой поверхности в результате построения образуются кольцевые зоны - зоны Френеля. Разность хода волн, приходящих в точку М от любой зоны Френеля, не превышает (по построению). Поэтому в двух соседних зонах всегда есть такие соответствующие волны, разность хода между которыми в точке схождения М равна  . В точке М эти волны встретятся в противофазе и погасят друг друга. Волны третьей зоны ослабят действие второй, а волны четвертой ослабят действие третьей и т.д. Дифракционная картина на экране будет иметь вид чередующихся светлых и темных концентрических колец. В центре картины наблюдается светлое пятно.
   

Получим выражение радиуса   зоны Френеля с номером k, отстоящей от источника S монохроматических волн длины λ на расстояние , а от точки наблюдения М - на расстояние . При этом учтем, что , . Введем обозначения: ; ; ; ; .

Из треугольника SOА по теореме Пифагора можем записать:

(1)
Из треугольника АОМ по теореме Пифагора можем записать:


В последнем выражении величиной можно пренебречь  по сравнению с другими слагаемыми. Тогда получим:

(2)

Из выражений (1) и (2) можем записать:









Отсюда:

(3)

Подставим (3) в (1):



Поскольку пренебрежимо мало, то можем записать:



Отсюда:



Проверим размерность:



Подставим данные:



Ответ: .
6. Распространяющийся в воде луч света падает на ледяную поверхность. Найти угол падения, если отраженный луч полностью поляризован. Показатель преломления воды 1,33, льда – 1,31.

Дано:





Найти:

– ?



Отраженный луч полностью поляризован при падении под углом равным углу Брюстера .

Согласно закону Брюстера имеем:



Где – абсолютный показатель преломления первой среды (воды); – абсолютный показатель преломления второй среды (льда).

Отсюда:



Подставим данные:



Ответ: .
7. Период дифракционной решетки 0,005 мм. Определить число наблюдаемых главных максимумов в спектре дифракционной решетки для длины волны 760 нм.

Дано:





Найти:



Решение



Запишем  формулу дифракционной решетки

( ) (1)

Величина  называется постоянной (периодом) дифракционной решетки;  – угол максимума данного цвета; – порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки; – длина волны.

Положим, что   при  . Тогда, получим из формулы (1):



Следует учесть, что общее количество максимумов картины дифракции справа и слава от центрального максимума одинаково и равно:



Необходимо учесть центральный максимум, поэтому суммарное число максимумов равно:



Проверим размерность:



Подставим данные:



Ответ: .

8. Температура абсолютно чёрного тела изменилась при нагревании от 1000 К до 3000 К. На сколько изменилась при этом длина волны, на которую приходится максимум спектральной плотности энергетической светимости?

Дано:





Найти:





Решение



Согласно закону Вина, длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела равна:



где – постоянная Вина; – температура.

Запишем это выражение для двух длин волн:





Из двух последних выражений можем записать:







Проверим размерность:



Подставим данные:



Ответ: .
9. Определить постоянную Планка, если известно, что фотоэлектроны, вырываемые с поверхности металла светом с частотой 2,2·10^-15 Гц, полностью задерживаются обратным потенциалом 6,6 В, а вырываемые светом с частотой 4,6·10^-15 Гц – потенциалом 16,5 В.

Дано:









Найти:



Решение

Запишем формулу Эйнштейна для фотоэффекта:



Где – постоянная Планка;  – частота света;  – работа выхода электрона из металла; – кинетическая энергия фотоэлектрона.

По закону сохранения энергии можем записать:



Где – абсолютное значение заряда электрона; – задерживающий потенциал.

Тогда из двух последних выражений имеем:



Запишем последнее выражение для двух частот:





Из двух последних выражений имеем:







<sub>Проверим размерность:



Подставим данные:</sub>



Ответ: .
10. Чему равно отношение максимальных комптоновских изменений длин волн при рассеянии фотонов на свободных электронах и на ядрах атомов водорода?

Дано:
Найти:



Решение



Согласно формулы Комптона, длина волны после рассеивания определяется выражением:



Где – угол рассеивания; – длина волны падающего фотона; – постоянная Планка; – скорость света в вакууме; – масса частицы.

Тогда изменение длины волны равно:



Максимальное значение будет при . Тогда, исходя из последнего выражения можем записать:



Запишем последнее выражение для рассеянии фотонов на свободных электронах и на ядрах атомов водовода:





Отсюда:





Проверим размерность:



Подставим данные, учитывая, что – масса электрона; – масса ядра атома протона:



Ответ: .