Электротехника. 04Лекция. 11. Замена нескольких параллельных ветвей, содержащих источники эдс и источники тока, одной эквивалентной

• Название: 11. Замена нескольких параллельных ветвей, содержащих источники эдс и источники тока, одной эквивалентной
• Анкор: Электротехника
• Дата: 23.11.2022
• Размер: 0.68 Mb.
• Имя файла: 04Лекция.doc
• Тип: Закон; #807915

§11. Замена нескольких параллельных ветвей, содержащих источники ЭДС и источники тока, одной эквивалентной.

Рассмотрим схему рис. 15 а,б – эквивалентная схема.

О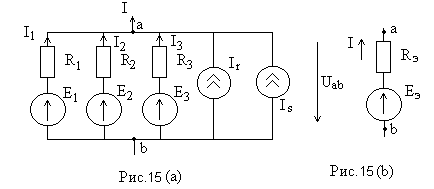
чевидно, что U_ab для схем (а)(б) одинаковые. Требуется найти R_э и E_э ,

По первому закону Кирхгофа:

I₁+I₂+I₃+I_r+I_s=I;

По второму закону Кирхгофа:

I₁=(E₁-Uab)/R₁=(E₁-U_ab)g₁

I₂=(E₂-U_ab)g₂

I_n=(En-U_ab)g_n;

С
ледовательно:
Где n- число параллельных ветвей с источниками ЭДС; g- число ветвей с источниками тока.

Для схемы рис. 15 б:

I=E_эg_э-U_abg_э; g_э=1/R_э (2)

Р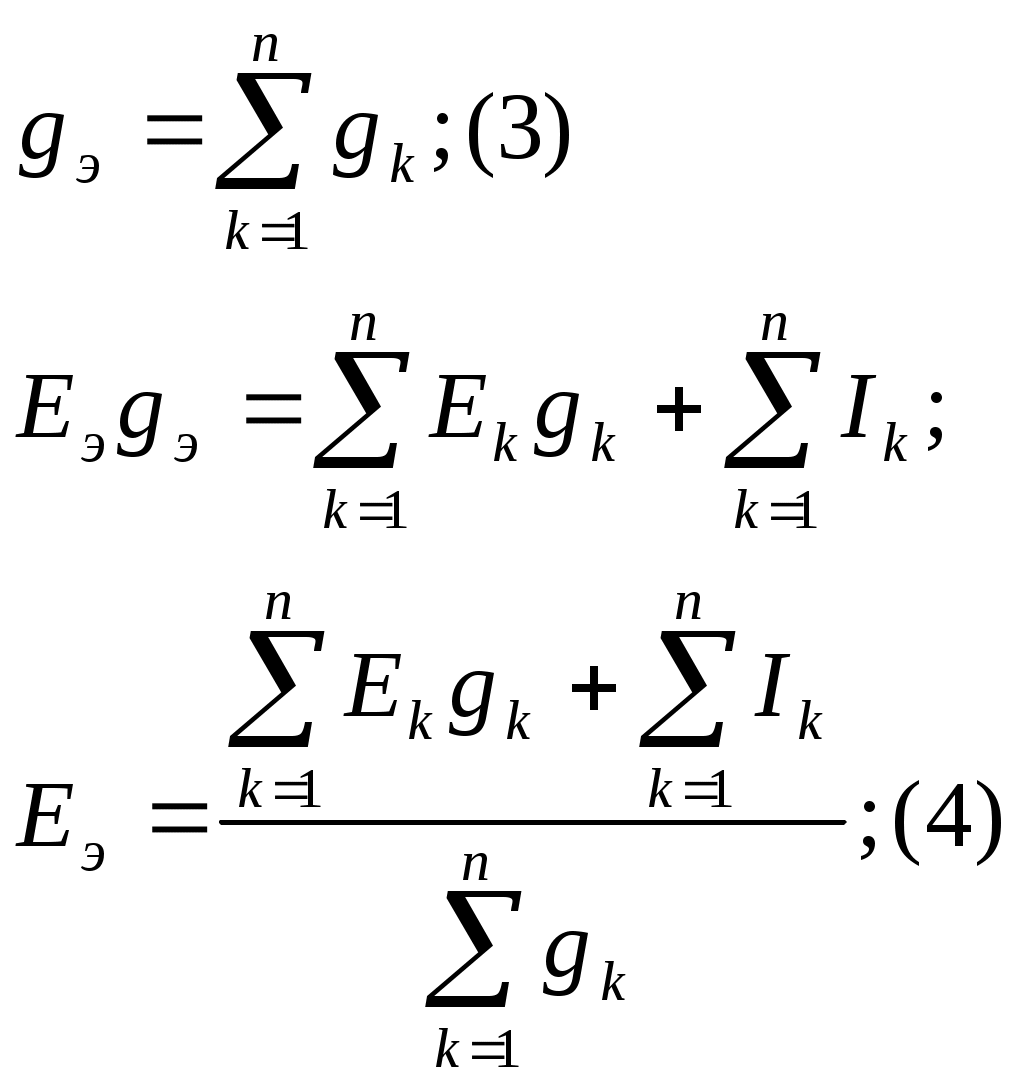
авенство токов I для схем (а), (б) рис. 15 должно иметь место при любых значениях U_ab, а это возможно только в том случае, когда коэффициенты при U_ab в (1), (2) равны.

Следовательно:

Формула (3) дает возможность найти проводимость g_э или R_э. Из формулы видно, что проводимость g_э не зависит от того, есть ли в ветвях схемы ЭДС или нет.

При использовании формулы (4) необходимо учитывать:

если в какой-либо ветви схемы ЭДС отсутствует, то соответствующее слагаемое в числителе выпадает, но проводимость этой ветви в знаменателе (4) остаётся;

если какая-либо ЭДС в исходной схеме имеет направление противоположное току, то соответствующее слагаемое войдет в числитель (4) со знаком минус.

Ветви схемы рис. 15 эквивалентны только в смысле поведения их по отношению ко всей остальной части схемы, но они не эквивалентны в отношении мощности.

Действительно, в ветвях схемы рис. 15(а) токи I₁, I₂ и т.д. могут протекать даже при I=0, тогда как в ветвях ab схемы рис. 15(b) при I=0 ток и потребление энергии отсутствуют.

§12. Метод двух узлов.

Часто встречаются схемы, содержащие два узла см. схему рис.10

Наиболее рациональным методом расчета таких схем является метод двух узлов.

В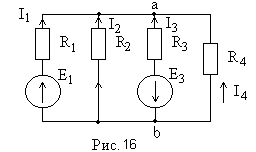
этом методе за основу берется напряжение между двумя узлами U_ab, затем через него находят остальные токи.

Р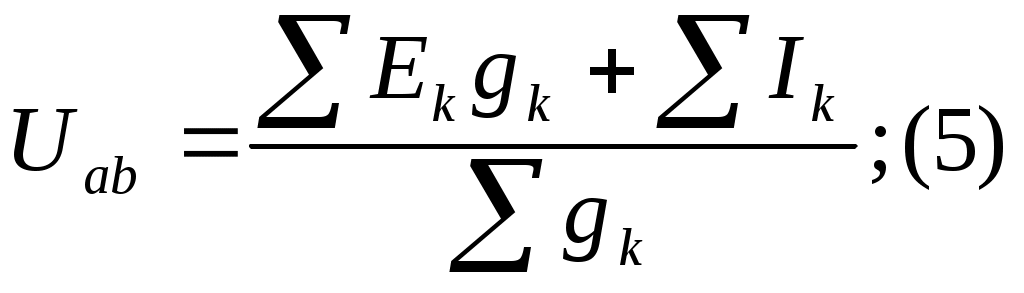
асчетные формулы получают из уравнения (1), при дополнительном условии I=0, тогда уравнение (1) преобразуется к виду:

После определения напряжения U_ab находим ток в любой ветви по формуле:

I_q=(E_q-U_ab)g_q

§13. Преобразование звезды в треугольник и наоборот.

Н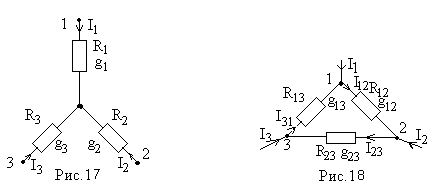
а рис. 17 показано соединение звездой и на рис. 18 соединение треугольником.

Узлы 1, 2, 3 обоих схем подключены к остальной части схемы ( не показаны).

Часто при расчете ЭЦ требуется преобразовать “звезду” в “треугольник” или наоборот. На обоих схемах к узлам 1, 2, 3 приходят токи I₁, I₂, I₃ соответственно.

Тогда уже “звезда”. 1 закон Кирхгофа:

I
₁+I₂+I₃=0 (1)



и через потенциалы точек 0,1, 2, 3 получим:

п
одставляя (2) в (1) получим:

о
тсюда:

тогда I₁:

Д
ля треугольника в соответствии с рис.18:

I₁=I₁₂-I₃₁=( φ₁- φ₂)g₁₂-( φ₃- φ₁)g₁₃= φ₁(g₁₂+g₁₃)- φ₃g₁₃- φ₂g₁₂; (5)

Т.к. токи I₁ рис.17 равен I₁ рис.18 при любых значениях потенциалов φ₁, φ₂, φ₃, то коэффициенты при φ₂ в правой части (5) должен равняться коэффициенту при φ₂ в правой части (4), аналогично для коэффициента приφ₂ в (5) и (4):

следовательно:

g₁₂=g₁g₂/(g₁+g₂+g₃) (6)

g₁₃=g₁g₃/(g₁+g₂+g₃) (7)

аналогично:

g₂₃=g₂g₃/(g₁+g₂+g₃) (8)

Формулы (6)-(8) дают возможность найти проводимости сторон “треугольника” через проводимости “звезды”.

Получим обратные соотношения:

R₁=1/g₁; R₂=1/g₂; R₃=1/g₃ - для “звезды”

R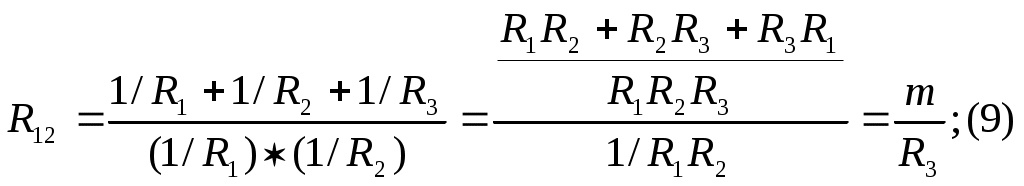
₁₂=1/g₁₂; R₂₃=1/g₂₃; R₁₃=1/g₁₃ -для “треугольника”

Из (6)-(8) получим:

где m=R₁R₂+R₂R₃+R₃R₁ (12)

R₂₃=m/R₁; (10)

R₁₃=m/R₂; (11)

С
оотношения (9)-(11) подставим в (12):

С
ледовательно:

П

одставляя m в уравнения (9), (10), (11), получим