тлэц 4-хполюсникик теория. 12. Основы теории четырехполюсников
 Скачать 372.27 Kb. Скачать 372.27 Kb.
|
|
Теория электрических цепей 12. Основы теории четырехполюсников 12.1. Общие положения 12.2. Уравнения передачи четырехполюсника 12.3. Применение матриц к расчету четырехполюсников 12.4. Параметры холостого хода и короткого замыкания четырехполюсника 12.5. Характеристические параметры четырехполюсника 12.6. Внешние характеристики четырехполюсника 12.7. Вопросы и задания для самопроверки  12.1. Общие положения В технике связи под четырехполюсником понимают электрическую цепь (или ее часть) любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии. Зажимы, к которым присоединяется приемник (нагрузка), - выходными зажимами (полюсами). В качестве примеров четырехполюсников можно привести трансформатор и усилитель. Четырехполюсниками являются электрические фильтры, усилительные устройства радиопередатчиков или радиоприемников, линия междугородной телефонной связи и т. д. Все эти устройства, имеющие совершенно "непохожие" схемы, обладают рядом общих свойств. 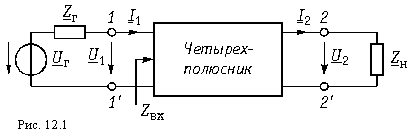 В общем, виде четырехполюсник изображают, как показано на рис. 12.1. Ко входу четырехполюсника 1-1' подключен источник электрической энергии с задающим напряжением Uг и внутренним сопротивлением Zг. К выходным зажимам 2-2' присоединена нагрузка с сопротивлением Zн. На входных зажимах действует напряжение U1; на выходных - U2. Через входные зажимы протекает ток I1, через выходные зажимы - I2. Заметим, что в роли источника и приемника электрической энергии могут выступать другие четырехполюсники. На рис. 12.1 использованы символические обозначения напряжений и токов, что справедливо при анализе четырехполюсника в режиме гармонических колебаний. Если же используется источник периодических негармонических или непериодических колебаний, то можно воспользоваться спектральным представлением напряжений и токов (см.5. Линейные электрические цепи в режиме периодических негармонических воздействий,9. Частотный метод анализа переходных процессов в линейных цепях) Подобное представление будем широко использовать при анализе частотных характеристик четырехполюсников. В необходимых случаях обращаться к операторным изображениям Uг(p), U1(p), U2(p), I1(p) и I2(p), которые легко получить, заменяя оператор jw на оператор р (см.7.4. Операторные передаточные функции). Различают четырехполюсники линейные и нелинейные. Линейные четырехполюсники отличаются от нелинейных тем, что не содержат нелинейных элементов (НЭ) и поэтому характеризуются линейной зависимостью напряжения и тока на выходных зажимах от напряжения и тока на входных зажимах. Примерами линейных четырехполюсников являются электрический фильтр, линия связи, трансформатор без сердечника; примерами нелинейных - преобразователь частоты (содержащий диоды) в радиоприемнике, выпрямитель переменного тока, трансформатор со стальным сердечником (при работе с насыщением стали). Усилитель, содержащий НЭ (например, триоды), может являться как линейным, так и нелинейным четырехполюсником в зависимости от режима его работы (на линейном или нелинейном участке характеристик триодов). 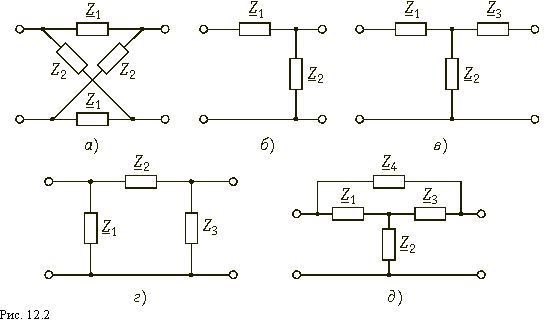 Четырехполюсники бывают пассивными и активными. Пассивные схемы не содержат источников электрической энергии, активные - содержат. Последние могут содержать зависимые и независимые источники. Примером активного четырехполюсника с зависимыми источниками может служить любой усилитель; примером пассивного - LC-фильтр. В зависимости от структуры различают четырехполюсники мостовые (рис. 12.2, а) и лестничные: гобразные (рис. 12.2, б), тобразные (рис. 12.2, в), побразные (рис. 12.2, г). Промежуточное положение занимают тобразномостовые (тперекрытые) схемы четырехполюсников (рис. 12.2, д). Четырехполюсники делятся на симметричные и несимметричные. В симметричном четырехполюснике перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи, с которой он соединен. Четырехполюсники, кроме электрической симметрии, могут иметь структурную симметрию, определяемую относительно вертикальной оси симметрии. Так, тобразный, побразный и тперекрытый четырехполюсники (рис. 12.2) имеют вертикальную ось симметрии при Z1 = Z3. Мостовая схема структурно симметрична. Очевидно, четырехполюсники, симметричные в структурном отношении, обладают электрической симметрией. Четырехполюсники могут быть уравновешенными и неуравновешенными. Уравновешенные четырехполюсники имеют горизонтальную ось симметрии (например, мостовая схема на рис. 12.2, а) и используются, когда необходимо сделать зажимы симметричными относительно какойлибо точки (например, земли). Можно сделать уравновешенной любую из лестничных схем четырехполюсников. Четырехполюсники также делятся на обратимые и необратимые. Обратимые четырехполюсники позволяют передавать энергию в обоих направлениях; для них справедлива теорема обратимости или взаимности, в соответствии с которой отношение напряжения на входе к току на выходе не меняется при перемене местами зажимов.  12.2. Уравнения передачи четырехполюсника Системы уравнений четырехполюсника. Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U1, U2, I1 и I2, называются уравнениями передачи четырехполюсника. Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсников. Сложная электрическая цепь (например, канал связи), имеющая входные и выходные зажимы, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Зная параметры этих четырехполюсников, можно вычислить параметры сложного четырехполюсника и получить тем самым зависимость между напряжениями и токами на зажимах результирующего сложного четырехполюсника, не производя расчетов всех напряжений и токов внутри заданной схемы. Кроме того, теория четырехполюсников позволяет решить обратную задачу: по заданным напряжениям и токам найти параметры четырехполюсника и затем построить его схему и рассчитать элементы, т. е. решить задачу синтеза. Пусть четырехполюсник содержит п независимых контуров. Отнесем первый контур ко входу четырехполюсника (Iк1 = I1), второй контур - к его выходу (Iк2 = I2). Будем считать, что во внутренних контурах четырехполюсника отсутствуют независимые источники энергии. При рассмотрении четырехполюсника важно заранее условиться о положительных направлениях напряжений и токов. В дальнейшем будем придерживаться положительных направлений, показанных стрелками на рис. 12.1, если особо не будут оговорены другие случаи. Составим систему уравнений для контурных токов: 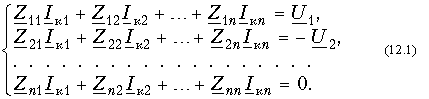 Определим из этой системы токи I1 и I2. 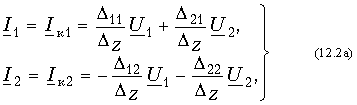 где DZ - определитель системы уравнений (12.1); D11, D22, D12 и D21 - алгебраические дополнения определителя DZ. Введем обозначения 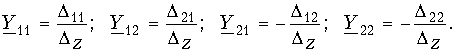 Тогда 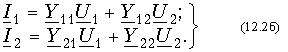 Коэффициенты Y11, Y12, Y21 и Y22 в уравнениях (12.2) называются Y-параметрами, или параметрами проводимостей четырехполюсника, так как по размерности они являются именно таковыми. Уравнения (12.2) называются уравнениями передачи четырехполюсника в Y-параметрах. Эти уравнения представляют собой одну из возможных форм уравнений передачи. Она позволяют находить любую пару из значений I1, I2, U1 и U2, если заданы значения другой пары. Помимо уравнений в форме (12.2) существует еще пять форм уравнений передачи. Уравнения, связывающие напряжения U1, U2 и токи I1, I2 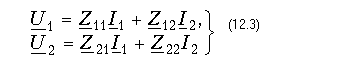 содержат в качестве коэффициентов параметры сопротивлений четырехполюсника, или Z-параметры, и называются уравнениями передачи в Z-параметрах. Параметры Z11, Z12, Z21 и Z22 имеют размерность сопротивлений. Заметим, что они не являются обратными величинами по отношению к параметрам проводимости, таким образом, например Не следует также путать эти параметры с собственными и взаимными сопротивлениями контуров Z11, Z12 и т. д. в уравнениях (12.1) для контурных токов. Коэффициенты, входящие в систему уравнений, связывающую входные U1 и I1 и выходные U2 и I2 напряжения и токи 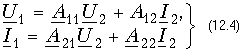 называются апараметрами, или обобщенными параметрами. Уравнения (12.4) называются уравнениями передачи в апараметрах. Параметры A11 и A22 являются безразмерными, параметр A12 имеет размерность сопротивления; параметр A21 - размерность проводимости. Приведем еще две формы уравнений передачи: 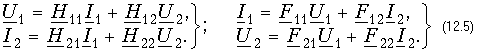 Коэффициенты H11, H12, H21 и H22 называются нпараметрами и применяются при рассмотрении схем с транзисторами. Параметры H12 и H21 являются безразмерными, а параметры H11 и H22 имеют размерности сопротивления и проводимости. Коэффициенты F11, F12, F21 и F22 называются F-параметрами и применяются при рассмотрении схем с электронными лампами. Параметры F12 и F21 безразмерные, а параметры F11 и F22 имеют размерности проводимости и сопротивления. Уравнения (12.5) называются соответственно уравнениями передачи в H-параметрах и F-параметрах. Все формы уравнений передачи принципиально равноправны. Выбор той или иной формы зависит исключительно от задачи, которая в данном случае решается. Полная совокупность параметров любой системы уравнений передачи образует систему параметров четырехполюсника. Так, систему Y-параметров четырехполюсника образует совокупность его параметров Y11, Y12, Y21, Y22. Два четырехполюсника, имеющие одинаковые системы параметров, независимо от их внутренней структуры, числа элементов и т. д., характеризуются, очевидно, одинаковыми уравнениями передачи. Такие четырехполюсники называются эквивалентными, и при включении любого из них между одними и теми же внешними цепями на их зажимах устанавливаются одинаковые режимы. Свойства параметровкоэффициентов. Системы Y-, Z-, а, н и F-параметров образованы из коэффициентов уравнений передачи, и поэтому часто их объединяют одним названием параметрыкоэффициенты. Рассмотрим основные свойства параметровкоэффициентов. 1. Параметрыкоэффициенты определяются только схемой четырехполюсника и ее элементами и не зависят от внешних цепей, между которыми может быть включен четырехполюсник, т. е. они характеризуют собственно четырехполюсник. Пример. На входе гобразного четырехполюсника (см. рис. 12.2, б), подключенного к внешним цепям, действует напряжение U1 и ток I1, а на выходе напряжение U2 и ток I2. Определим апараметры четырехполюсника. В соответствии с ЗНК и 3TK U1 = U2 + I1Z1 и I1 = U2/Z2 + I2. Подставляя выражение для тока I1 в первое равенство, получаем Сравнивая эти уравнения с уравнениями передачи в апараметрах (12.4), находим . Как видим, апараметры определяются только элементами гобразного четырехполюсника и не зависят от внешних воздействий. 2. Все системы параметровкоэффициентов описывают один и тот же четырехполюсник, поэтому между различными системами параметровкоэффициентов существует однозначная взаимосвязь. Пример. Установим связь между апараметрами и Z-параметрами. Решая систему уравнений в Z-параметрах (12.3) относительно неизвестных U1 и I1, находим: 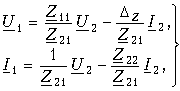 где DZ = Z11Z22 - Z12Z21 - определитель системы уравнений (12.3). Сравнивая эту систему уравнений с системой (12.4), устанавливаем, что A11 = Z11/Z22; A12 = -DZ/Z21; A21 = 1/Z21 и A22 = -Z22/Z21. Решая систему (12.4) относительно неизвестных U1 и U2, можно найти выражение Z-параметров через апараметры: где DA = A11A22 - A12A21 - определитель системы уравнений (12.4). Аналогичным образом можно установить связь между другими системами параметров. В табл. 12.1 приведены соотношения между различными системами параметровкоэффициентов. 3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами. Действительно, в многоконтурной схеме пассивного четырехполюсника взаимные сопротивления Zkm и Zmk k-го и m-го контуров равны между собой. Следовательно, Y12 = -Y21. Зная связь между Y-параметрами и Z-параметрами, можно установить, что Z12 = -Z21. Далее можно показать, что для апараметров справедливо соотношение 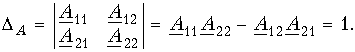 Это легко доказать, если выразить в данном определителе апара-метры, например, через Z-параметры. Наконец, аналогичным образом можно найти, что H12 = H21 и F12 = F21. Таким образом, независимыми параметрами четырехполюсника могут быть: Y11, Y12 = -Y21, Y22; Z11, Z12 = -Z21, Z22; H11, H12 = = H21, H22; F11, F12 = F21 и F22 или любые три из параметров A11, A12, A21 и A22. 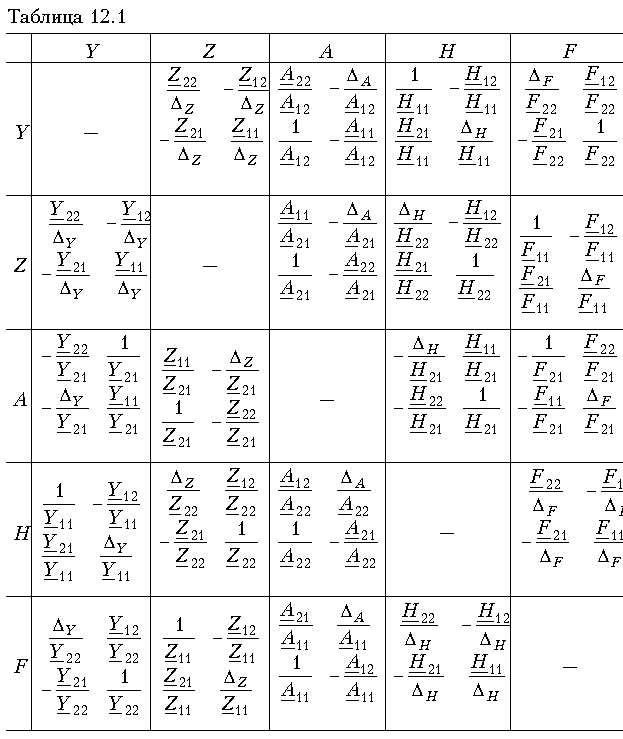 4. При изменении направления передачи энергии через четырехполюсник во всех выражениях, включающих апараметры, коэффициенты A11 и A22 меняются местами. Рассмотрим передачу энергии через четырехполюсник в обратном направлении, т. е. от зажимов 2-2' к зажимам 1-1' (рис. 12.3). Если в уравнениях передачи (12.4) заменить напряжение U1 и ток I1 на зажимах 1-1' на напряжение U2' и ток -I2' в соответствии с рис. 12.3, а напряжение U2 и ток I2 на зажимах 2-2' на величины -U1' и -I1', то (12.4) можно переписать в виде 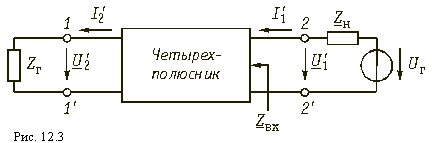 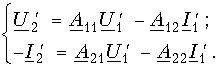 Решая эту систему относительно нового входа четырехполюсника, т. е. относительно переменных U1' и I1', получаем 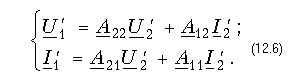 Сопоставляя эти уравнения с (12.4), можно сделать интересное наблюдение: в уравнениях передачи параметры A11 и A22 поменялись местами. Оказывается, этот факт справедлив не только для уравнений передачи, но и для любых других выражений, в которые входят апараметры. 5. Симметричные пассивные четырехполюсники имеют только два независимых параметра. В самом деле, в случае симметричного пассивного четырехполюсника не имеет значения направление передачи энергии: напряжения и токи на входе и выходе не изменяются при замене местами зажимов. Сравнивая уравнения передачи (12.4) и (12.6), устанавливаем, что A11 = A22. Из табл. 12.1 находим также, что в симметричных четырехполюсниках Y11 = = -Y22; Z11 = -Z22 и DH = -1. Любой симметричный пассивный четырехполюсник полностью описывается двумя независимыми параметрами: A11 = A22 и любым из параметров A12 и A21 (так как они связаны уравнением A11A22 - - A12A21 = 1); Y11 = -Y22 и Y12 = -Y21; Z11 = -Z22 и Z12 = -Z21; H12 = H21 и любым из параметров H11 и H22 (так как для симметричных четырехполюсников H11H22 - H12H21 = -1); F12 = F21 и любым из параметров F11 и F22. 6. Параметрыкоэффициенты имеют определенный физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи содержат лишь один интересующий нас параметр. Подобное произойдет, если использовать режимы холостого хода (XX -размыкания пары зажимов) и короткого замыкания (КЗ - замыкания накоротко пары зажимов). Так, при XX на зажимах 2-2' (см. рис. 12.1) ток I2 = 0. Тогда уравнения передачи, содержащие ток I2, например уравнения (12.3) в Z-параметрах, имеют вид: Коэффициент Z11 = U1/I1 при I2 = 0 есть входное сопротивление четырехполюсника, измеренное со стороны зажимов 1-1' при разомкнутых зажимах 2-2' или входное сопротивление XX. Коэффициент - отношение комплексного действующего напряжения на разомкнутых зажимах 2-2' четырехполюсника к комплексному действующему току, протекающему через зажимы 1-1', или взаимное (передаточное) сопротивление XX. Рассматривая режим XX на зажимах 1-1' (I1 = 0), убеждаемся из уравнений (12.3), что Z22 - выходное сопротивление четырехполюсника при разомкнутых входных зажимах, a Z12 - взаимное (передаточное) сопротивление при XX на зажимах 1-1'. Предлагаем читателю самостоятельно установить физический смысл остальных параметров, "устраивая" поочередно XX на зажимах 2-2' (I2 = 0) и зажимах 1-1' (I1 = 0) и КЗ на этих же зажимах (U2 = 0 и U1 = 0) и используя соответствующие уравнения передачи (12.2), (12.4) и (12.5). 7. Из предыдущего свойства следует, что параметрыкоэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд (действующих значений) напряжений и токов. В случае анализа четырехполюсника в режиме негармонических колебаний используют спектральные представления электрических величин. Можно показать, что параметрыкоэффициенты, рассматриваемые относительно не отдельной частоты, а определенного спектра частот, являются рациональными функциями оператора jw. При переходе от оператора jw к оператору р параметрыкоэффициенты представляют собой рациональные функции оператора р. Пример. Для четырехполюсника на рис. 12.2, б определим параметр Z11. Исходя из физического смысла параметра Z11 (он является входным сопротивлением гобразной схемы при разомкнутых зажимах на выходе), определяем из рис. 12.2, б: Z11 = Z1 + Z2. Этот же результат можно получить следующим образом: 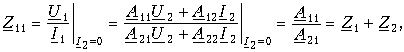 где значения параметров A11 и A21 взяты из первого примера этой главы. Пусть далее двухполюсник Z1 состоит только из индуктивности L, а двухполюсник Z2 - только из емкости С. Тогда, используя операторную форму записи, получаем 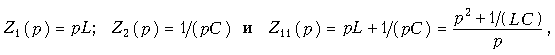 т. е. Z11 является дробнорациональной функцией оператора р с положительными вещественными коэффициентами. Нули этой функции - мнимые и лежат на мнимой оси комплексной плоскости, полюс р1 = 0. При замене оператора р оператором jw переходим к частотной характеристике Полученные выражения Z11(р) и Z11(jw) напоминают выражение входного сопротивления последовательного LC-контура. Это объясняется тем, что входное сопротивление гобразной цепи (см. рис. 12.2, б) при разомкнутых зажимах определяется последовательным соединением двухполюсников Z1, и Z2 (индуктивности и емкости), т. е. Z11 является сопротивлением двухполюсника (ср. с (4.115)).  |
