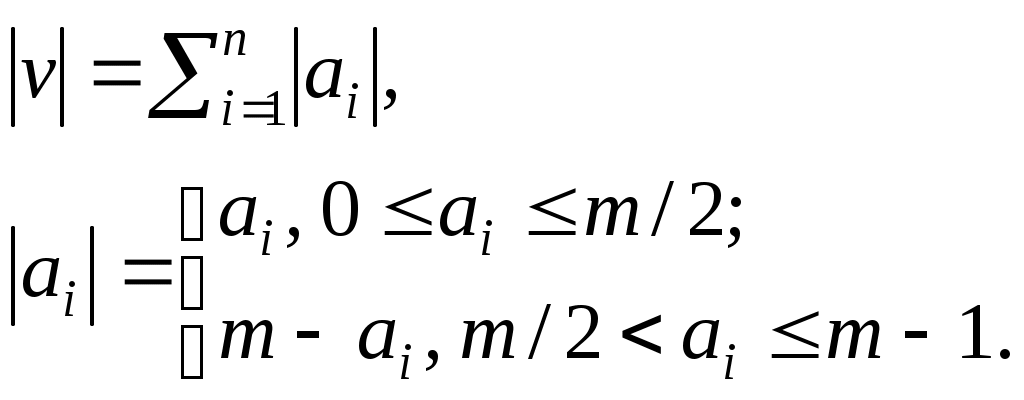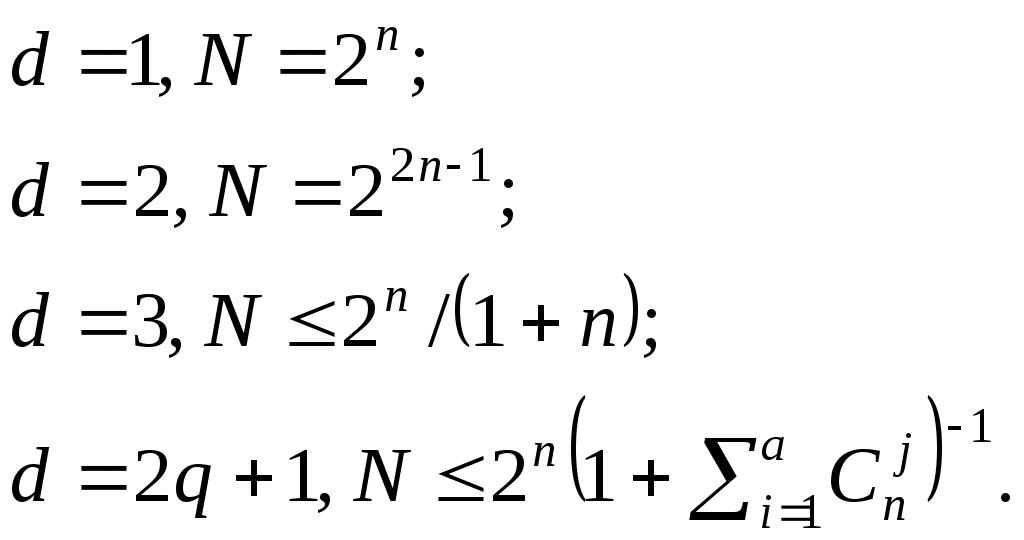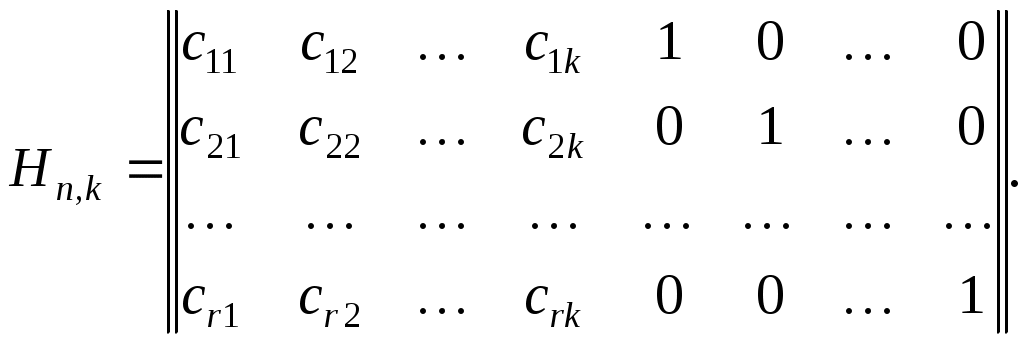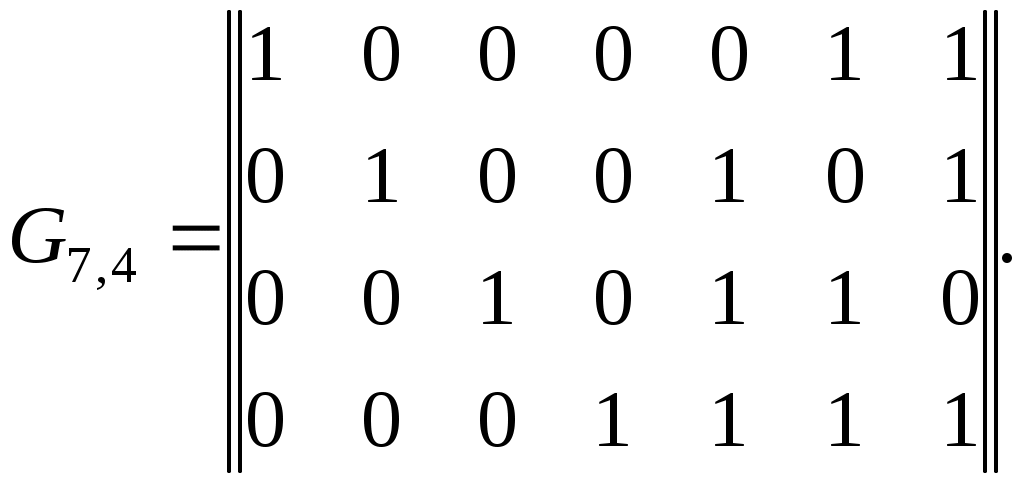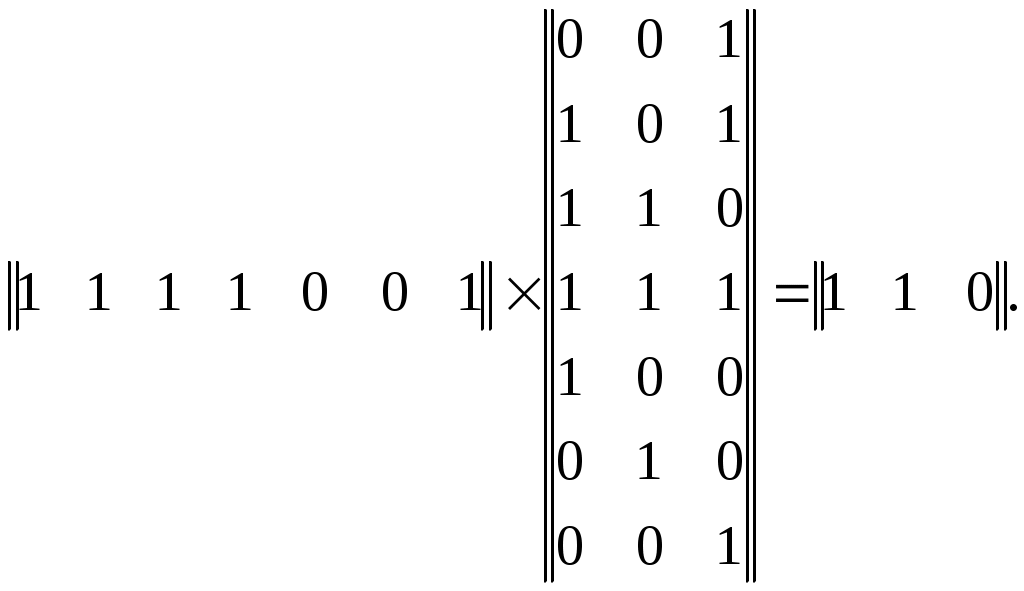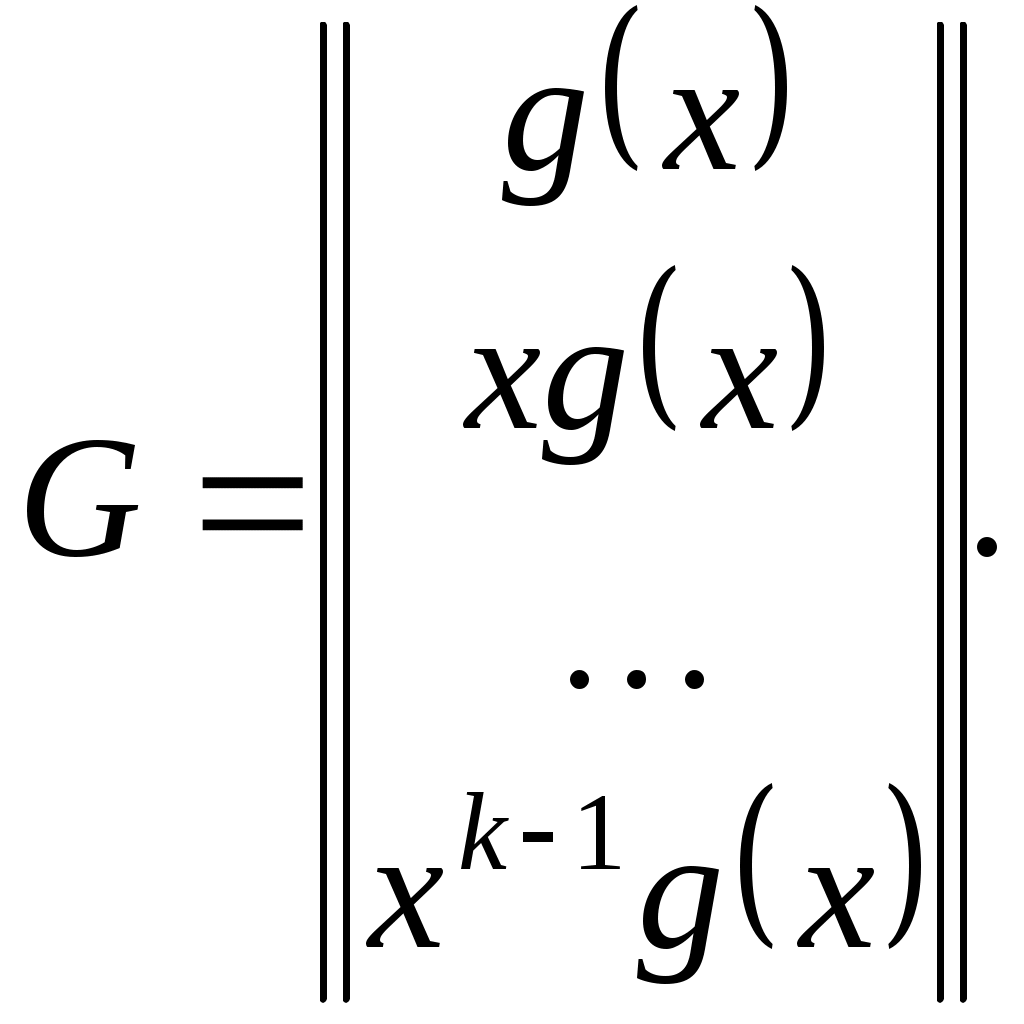кодирование. Лекция 13 - Помехоустойчивое кодирование. 13 помехоустойчивое кодирование

• Название: 13 помехоустойчивое кодирование
• Анкор: кодирование
• Дата: 11.12.2022
• Размер: 206 Kb.
• Имя файла: Лекция 13 - Помехоустойчивое кодирование.doc
• Тип: Документы; #839770

13 ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

При передаче информации по каналу с шумом возможно искажение части передаваемых разрядов. Помехоустойчивое кодирование позволяет добиться, чтобы при некоторых условиях такие искажения автоматически исправлялись, или, по крайней мере, обнаруживались.

13.1 Основные понятия

Теорема Шеннона утверждает, что если скорость передачи информации источником меньше или равна пропускной способности канала, то существует код, обеспечивающий передачу информации по каналу со сколь угодно малой частотой ошибок. Однако с её помощью не решается вопрос, как следует кодировать сообщения, чтобы добиться при максимальной скорости передачи минимального количества ошибок, то есть не решается проблемы помехоустойчивого кодирования. Для решения этой проблемы используются специальные методы. Широкое распространение получили алгебраические методы, с помощью которых, в частности, исследован широкий класс так называемых групповых кодов, а также геометрические методы, при которых кодовые комбинации представляются в виде элементов некоторого абстрактного пространства, называемого кодовым пространством.

Рассмотрим построение кодового пространства применительно к равномерным кодам, в частности, к блочным, кодовые комбинации которых кодируются и декодируются независимо друг от друга. Пусть выходной алфавит B равномерного n-значного кода Г состоит из m символов; число m называется основанием кода. Кодовая комбинация такого кода имеет вид a₁a₂…a_n, где a_i – значение i-го разряда кода, i = 1, 2, …, n, . Упорядочим произвольно символы алфавита . Индекс класса поставим в соответствие значению остатка от деления любого представителя класса на m. Введём на множестве B две алгебраические операции: умножение и сложение, понимая под произведением классов класс , где r – остаток от деления произведения kj на m, и под суммой классов класс при k + j < m и класс при k + j ≤ m. Множество с введёнными операциями сложения и умножения является полем, что позволяет кодовые комбинации над алфавитом B рассматривать как векторы в n-мерном пространстве над полем B. Это пространство также называется кодовым пространством, а его элементы – кодовыми векторами.

При анализе воздействия ошибок на кодовые векторы в кодовом пространстве вводятся метрики. Наиболее часто применяются метрики Ли и Хэмминга. Для определения метрики Ли используется понятие веса вектора v = a₁a₂…a_n, где :

Расстоянием Ли d(v_j, v_k) между векторами v_j = a₁a₂…a_n и v_k = b₁b₂…b_n называется вес разности векторов v_j и v_k:

(13.1)

При построении большинства наиболее употребимых блочных кодов используется метрика Хэмминга. Вес вектора v, по Хэммингу, равен числу ненулевых разрядов этого вектора, а расстояние Хемминга между векторами v_j и v_k определяется как вес разности векторов v_j и v_k. Следует отметить, что при m = 2 и m = 3 расстояния Хэмминга и Ли совпадают.

Кодовое пространство n-разрядного кода с основанием m содержит mⁿ векторов. При передаче информации, как правило, используются не все возможные комбинации, а лишь некоторое их подмножество V₁ = {v₁, v₂, …, v_N}, где N < mⁿ. Обозначим расстояние между парой векторов V₁ символом d(v_i, v_j), где i, j = 1, 2, …, N, i ≠ j. Величина min d(v_i, v_j) называется минимальным кодовым расстоянием и обозначается символом d.

В системах передачи и хранения данных обычно используют бинарные коды, то есть коды с основанием 2: B = {0, 1}. Определим минимальное кодовое расстояние системы векторов V = {11001, 01101, 01110, 00000}. Для бинарного кода операцию вычитания в выражении (13.1) можно заменить сложением по модулю 2. Расстояние между нулевой комбинацией и всеми остальными равно 3, то есть числу единиц в каждой из комбинаций. Для остальных векторов

11001+01101 = 10100,

11001+01110 = 10111,

01101+01110 = 00011.

Минимальное число единиц в результирующих векторах равно 2, следовательно, минимальное кодовое расстояния d = 2.

Для анализа действия помех на передаваемый кодовый вектор вводят понятие вектора ошибки. Кодовый вектор v₁ и вектор ошибки e складываются по модулю 2, после чего получается искажённый вектор v₁'. Например, если v₁ = 11111 и e = 01000, то v₁' = 10111. Следовательно, в разрядах передаваемой кодовой комбинации, соответствующих единичным разрядам вектора e, возникают ошибки.

При исследовании процесса возникновения ошибок в дискретном канале используют математические модели ошибок, которые представляют собой распределение вероятностей по всем возможным векторам ошибки. В качестве примера рассмотрим одну из самых распространённых моделей, которая основана на статистической гипотезе о том, что в каждом разряде вектора ошибки единица появляется с вероятностью p независимо от того, какие значения получили остальные разряды вектора ошибки. Величина, равная количеству единиц в векторе ошибки называется кратностью и обозначается символом q. Из теории вероятностей известно, что выдвинутой статистической гипотезе соответствует биномиальный закон распределения кратности ошибки. Поэтому математической моделью ошибки может служить выражение , определяющая вероятность того, что при передаче по дискретному каналу в кодовой комбинации бинарного кода длины n возникнет ошибка кратности q.

Определим вероятности появления ошибок кратности0, 1, 2, 3, 4, 5 в кодовой комбинации длины 5 бинарного кода, если вероятность ошибочного приёма разряда равна 0,1. Используя биномиальный закон распределения получаем, что P_5,0 = 0,56, P_5,1 = 0,33, P_5,2 = 0,07, P_5,3 = 0,008, P_5,4 = 0,00004, P_5,5 = 0,00001. Отсюда видно, что вероятность появления ошибок большой кратности мала. Наиболее часто появляются ошибки кратности 1.

Математические модели ошибок должны отражать реальные процессы, происходящие в канале связи, и строиться на статистике помех. Чем точнее математическая модель описывает действительность, тем точнее можно получить оценки относительно спроектированного кода. Следует учесть, что эффективность того или иного помехоустойчивого кода зависит от вида помех, действующего в канале связи. Код может быть весьма эффективным (число необнаруженных помех будет очень мало) при одной статистике помех и очень плохим при другой. Поэтому при проектировании помехоустойчивых кодов необходимо ориентироваться на определённый вид помех и в соответствии с этим в качестве исходной иметь определённую модель ошибок.

13.2 Обнаружение и исправление ошибок

Наибольшее распространение при передаче сообщений получили блочные равномерные коды. Помехоустойчивость блочных кодов, как и других кодов, основывается на введении избыточности в кодовые комбинации. Коды, не обладающие избыточностью, не способны обнаруживать и тем более исправлять ошибки.

В безызбыточных равномерных кодах длины k все 2^k возможных кодовых комбинаций используются, то есть любой из 2^k кодовой комбинации сопоставляется какой-либо символ внешнего алфавита. Такие коды получили название первичных кодов. Ошибка любой кратности в какой-либо кодовой комбинации всегда приводит к ошибочному декодированию этой кодовой комбинации.

Для обеспечения помехоустойчивости кода вводят дополнительные разряды. Если, например, для кодирования всех символов внешнего алфавита достаточно иметь k-разрядный первичный код, то для обеспечения помехоустойчивости к разрядам первичного кода добавляется r избыточных разрядов. При этом длина результирующей кодовой комбинации становится равной n = k + r. Избыточные коды делятся на разделимые и неразделимые.

В разделимых кодах роль разрядов кодовой комбинации разграничена: часть разрядов, часто совпадающая с разрядами исходного первичного кода, являются информационными, остальные разряды играют роль проверочных разрядов. В неразделимых кодах все разряды равноправные, и в кодовой комбинации нельзя отделить информационные разряды от проверочных. Примером неразделимого кода может служить код с постоянным весом «3 из 7». Особенностью этого кода является то, что в любой его кодовой комбинации длины 7 имеется ровно три единицы. Обнаруживающая способность данного кода основывается на том, что любая одиночная ошибка изменяет количество единиц в кодовой комбинации.

Можно сказать, что помехоустойчивость достигается тем, что для кодирования используются не все кодовые комбинации, а только часть из них (для разделимых кодов эта часть равна 2^k). Остальные кодовые комбинации называются запрещёнными и при передаче информации не используются. Если d > 1, то любая одиночная ошибка будет переводить разрешённую комбинацию в запрещённую, наличие которой на принимающей стороне может служить индикатором ошибки.

При разработке реальных кодов учитывается статистика помех и требование верности передачи информации. Верность передачи оценивается часто как среднее число верно принятых кодовых комбинаций, приходящихся на одну ошибочно принятую, или как вероятность верного приёма кодовой комбинации.

Примером блочного разделимого кода может служить код с проверкой на чётность. Кодовая комбинация такого кода имеет вид a₁a₂…a_kb. Первые k разрядов являются информационными, и, как правило, совпадают с разрядами исходного первичного кода. Последний разряд является избыточным и определяется как результат сложения по модулю 2 всех информационных разрядов. Если число единиц в информационных разрядах чётное, то b = 0, в противном случае b = 1. Такой код обеспечивает значение d = 2 и обладает способностью обнаруживать все ошибки кратности 1.

Для оценки качества кодов применяют коэффициент избыточности и коэффициент повышения верности. Коэффициент избыточности определяется выражением

где H_max – максимальная энтропия n-разрядного равномерного кода с числом кодовых комбинаций M = 2ⁿ, при этом H_max = log₂M = n. Под H(x) понимают максимальную энтропию разрешённых кодовых комбинаций, число которых обозначают через N, тогда H(X) = log N. Для неразделимого кода:

(13.2)

Например, для кода «3 из 7» максимальное количество кодовых комбинаций составляет 2⁷. Число разрешённых кодовых комбинаций . Тогда коэффициент избыточности равен:

Для разделимых кодов формула упрощается:

где n – длина кодовой комбинации, k – число информационных разрядов. Для n-разрядного кода с проверкой чётности получаем, что K_и = 1/n.

Коэффициент избыточности принимает значение от 0 (отсутствие избыточности) до 1 (избыточность неограниченно велика). Коэффициент избыточности характеризует качество помехоустойчивого кода: чем меньше избыточность кода при прочих равных условиях, тем код лучше.

Коэффициент повышения верности определяется как отношение вероятности появления ошибочных кодовых комбинаций на выходе дискретного канала к вероятности появления необнаруженных ошибок.

Помехоустойчивые коды позволяют не только обнаруживать ошибки, но и исправлять их. Общая идея исправления ошибок кратности на более q_m заключается в следующем. Число возможных кодовых комбинаций M помехоустойчивого кода разбивается на N классов по числу разрешённых кодовых комбинаций. Разбиение осуществляется таким образом, чтобы в каждый класс входили одна разрешённая кодовая комбинация и ближайшие к ней запрещённые. При декодировании определяется, какому классу принадлежит принятая кодовая комбинация. Если кодовая комбинация принята с ошибкой, то есть является запрещённой, то она исправляется на разрешённую кодовую комбинацию, принадлежащую тому же классу.

Для обеспечения возможности исправления ошибок кратности не более q_m кодовое расстояние должно быть больше 2q_m. Обычно оно выбирается по формуле d = 2q_m+1. Актуальной является задача определения наибольшего числа N кодовых комбинаций n-разрядного двоичного кода с кодовым расстоянием d. В теории кодирования существуют следующие оценки:

Оценим корректирующий код, исправляющий одиночные ошибки (q_m=1) на основе 4-разрядного двоичного кода, общее число комбинаций которого равно 16. Среди этих 16 кодовых комбинаций нужно выбрать максимальное число разрешённых комбинаций, отстоящих друг от друга на расстояние не меньше, чем d = 2q_m+1 = 3. Оценим верхнюю границу количества разрешённых кодовых комбинаций: N≤ 2ⁿ/(1+n) = 3. На самом деле их нельзя найти больше двух.

13.3 Матричное представление (n, k)-кодов.

Среди блочных кодов широкое распространение получили линейные коды. Для определения линейного кода воспользуемся представлением кодовых комбинаций в виде элементов n-мерного векторного пространства V над полем P. Под полем P понимают символы выходного алфавита (внутреннего алфавита системы), число которых равно m. Линейными m-ичными кодами называются k-мерные подпространства n-мерного пространства V. При этом число n имеет смысл длины кодовой комбинации, число k определяет число информационных разрядов. Линейные коды называют также (n, k)-кодами.

Среди линейных кодов особую роль играют групповые коды, для которых m = 2 (двоичные коды). Существуют различные способы задания групповых кодов. Наиболее распространены матричное описание кодов и задание их с помощью порождающих многочленов.

Запишем кодовую комбинацию в виде a₁a₂…a_kb₁b₂…b_r. Первые k-разрядов являются информационными, остальные – проверочными. Проверочные символы кодовых комбинаций формируются из информационных символов на основе выражения

(13.3)

Здесь коэффициенты c_j1, c_j2, …, c_jk принимают значения из множества {0, 1}.

Любая кодовая комбинация, состоящая из k информационных разрядов, все проверочные разряды которой составлены в соответствие с формулой (13.3), является разрешённой комбинацией (n, k)-кода.

Пусть u и v – две разрешённые комбинации группового (n, k)-кода. Тогда кодовая комбинация w = u + v также является разрешённой комбинацией этого кода. Действительно, пусть

Тогда

,

где

Следовательно, проверочные разряды b_j'' кодовой комбинации w формируются в соответствии с выражением (13.3), поэтому кодовая комбинация w также является разрешённой.

Любые k линейно независимых векторов n-мерного линейного векторного пространства порождают k-мерное подпространство, образуя базис этого подпространства. Отсюда следует, что для задания (n, k)-кода достаточно выбрать k любых линейно независимых разрешённых кодовых комбинаций, а остальные разрешённые кодовые комбинации получать как линейные комбинации выбранных базисных векторов.

Обычно для задания (n, k)-кода пользуются этой возможностью, представляя k линейно независимых кодовых комбинаций в форме матрицы. Такая матрица называется порождающей матрицей (n, k)-кода. В общем виде её можно представить следующим образом:

(13.4)

Порождающая матрица G_n,k двоичного кода порождает ровно 2^k разрешённых кодовых комбинаций.

В зависимости от выбранного базиса k-мерного подпространства n-мерного кодового пространства кодовое расстояние совокупности 2^k векторов будет различным. При проектировании (n, k) кода ставится задача оптимального размещения кодовых векторов в n-мерном кодовом пространстве в соответствии с заданной статистикой ошибок и, в частности, обеспечения максимально возможного кодового расстояния.

Пусть v₁, v₂, …, v_k – кодовые векторы-строки, составляющие порождающую матрицу

Тогда разрешённую кодовую комбинацию (n, k)-кода можно представить в виде линейной комбинации векторов

(13.5)

где g₁, g₂, …, g_k – коэффициенты, принимающие значения из множества {0, 1}.

Проверочные разряды b₁, …, b_r кодового вектора v, передаваемого по каналу связи, формируются в соответствии с (13.3). Это же соотношение может быть использовано на приёмном конце канала для проверки правильности кодовой комбинации: равенство (13.3) должно выполняться, если ошибки не произошло. С каждой принятой кодовой комбинацией можно связать систему проверок по числу проверочных разрядов, которая может быть описана следующей системой уравнений:

(13.6)

Здесь . Нули в правых частях равенств истолковываются как отсутствие ошибки в принятой кодовой комбинации v. Для удобства систему проверок (13.6) записывают в матричной форме, а именно как произведение вектор-строки v, соответствующей принятой кодовой комбинации, на матрицу проверочных коэффициентов:

Матрицу H_n,k называют проверочной матрицей. Система проверок (13.6) может быть записана в виде:

(13.7)

В общем случае результат умножения может быть отличен от нуля

где

Вектор-строка называется синдромом ошибки. Всего может быть 2^r–1 различных ненулевых синдромов, разбивающих множество возможных ошибок на 2^r–1 класса. Это позволяет по виду синдрома ошибки определять, к какому классу относится ошибка. Часто (n, k)-код проектируется таким образом, что с вероятностью, близкой к единице, каждый из выделенных 2^r–1 классов ошибок содержит всего по одному элементу. Такие коды позволяют исправлять ошибки.

Порождающая и проверочная матрица связаны между собой соотношением, что позволяет определять одну из них, если известна другая.

Если к какой-либо строке v_i порождающей матрицы G_n,k прибавить линейную комбинацию других строк, то от этого порождающая матрица не изменится в том смысле, что останется порождающей матрицей того же самого (n, k)-кода. Путём такой замены строк матрицу G_n,k можно привести к каноническому виду:

(13.8)

канонический вид порождающей матрицы удобен тем, что существует простая связь между элементами порождающей и проверочной матриц: для определения проверочной матрицы (n, k)-кода, порождаемого матрицей вида (13.8), нужно транспонировать подматрицу проверочных разрядов матрицы G_n,k и приписать справа к полученной матрице единичную матрицу размерности . Следовательно, матрице (13.8) соответствует проверочная матрица:

13.4 Код Хэмминга

В качестве примера (n, k)-кода, при задании которого используется матричное представление, рассмотрим код Хэмминга – код с кодовым расстоянием d = 3, позволяющий исправлять все одиночные ошибки. Для кода Хэмминга число разрешённых кодовых комбинаций равно верхней границе – 2ⁿ/(n+ 1). Первые k разрядов кодовых комбинация используются в качестве информационных, их число равно:

.

Данное уравнение имеет целочисленные решения k = 0, 1, 4, 11, 26, …, которые и определяют соответствующие коды Хэмминга: (3, 1), (7, 4), (15,11) и т.д. Рассмотрим построение (7, 4)-кода. Для этого воспользуемся каноническим представлением порождающей матрицы. Одним из свойств порождающей матрицы является то, что для различных кодовых комбинаций, составленных из информационных разрядов, должны быть различными и проверочные разряды. Так как все вектор-строки единичной подматрицы матрицы G_n,k различны, то и подматрица проверочных разрядов должна состоять из различных ненулевых строк (общее число ненулевых строк должно быть равно 2^r–1).

Вычтем из возможного числа ненулевых строк r строк, образующих единичную матрицу , которую следует добавить к транспонированной подматрице проверочных разрядов при определении проверочной матрицы. Тогда останется 2^r–1–r r-разрядных строк с числом единиц не меньше двух. Для кода Хэмминга это число как раз равно числу информационных разрядов. Для (n, k)-кода число различных r-разрядных строк с числом единиц не меньше двух равно числу строк в порождающей матрице. Это свойство позволяет составить непосредственно один из вариантов порождающей матрицы (7, 4)-кода, например, такой:

Учитывая связь элементов порождающей и проверочной матриц, представленных в канонической форме, имеем:

Проверим способность разработанного (7, 4) кода исправлять одиночные ошибки. Пусть передаваемая кодовая комбинация v (7, 4)-кода образована путём сложения первой, второй и четвёртой строк матрицы G_7,4, тогда v = 1101001.

Предположим, что при передаче по каналу произошла ошибка в третьем разряде кодовой комбинации v. В этом случае на приёмной стороне канала будет получена кодовая комбинация v' = 1111001. Умножим принятую кодовую комбинацию на транспонированную проверочную матрицу H_7,4:

Отличие от нуля синдрома говорит о том, что произошла ошибка. Чтобы определить, в каком разряде кодовой комбинации произошла ошибка, проверим, с какой строкой матрицы транспонированной матрицы H_7,4 совпадает синдром. Как видно, он совпадает с третьей строкой. Следовательно, ошибка произошла в третьем разряде кодовой комбинации. В декодирующих устройствах систем передачи информации результат перемножения принятой кодовой комбинации на проверочную матрицу (синдром ошибки) используется для автоматического исправления соответствующего разряда.

13.5 Циклические коды

Циклическим кодом называется линейный код, который представляет собой конечное множество, замкнутое относительно операции циклического сдвига кодовых векторов, образующих его. Пусть дан n-мерный вектор v = a₀a₁…a_n-1 с координатами из конечного поля F. Его циклическим сдвигом называется вектор v' = a_n­-1a₀a₁…a_n-2.

Рассмотрим n-мерное арифметическое пространство над полем Галуа GF(2). Каждому вектору a₀a₁…a_n-1 из GF(2) можно сопоставить взаимно однозначно многочлен a₀+a₁x+…+a_n-1x^n-1 с коэффициентами из GF(2). Сумме двух векторов a₀a₁…a_n-1 и b₀b₁…b_n-1 ставится в соответствие сумма соответствующих им многочленов, произведению элементов поля на вектор - произведение многочлена, соответствующего этому вектору, на элемент.

Рассмотрим некоторый многочлен g(x) из описанного линейного пространства. Множество всех многочленов из этого подпространства, которые делятся без остатка на g(x), образует линейное подпространство. Линейное подпространство определяет некоторый линейный код.

Линейный код, образованный классом многочленов C(g(x)), кратных некоторому полиному g(x), называемому порождающим многочленом, называется полиномиальным.

Покажем, как связаны полиномиальные коды C(g(x)) и циклические коды. Пусть a = a₀…a_n-1 – некоторое кодовое слово, а соответствующий кодовый многочлен a(x) = a₀+...+a_n-1x^n-1. Циклическому сдвигу a' соответствует кодовый многочлен a'(x) = a_n-1+a₀x+…+a_n-2x^n-1, который можно выразить через первоначальный:

Поскольку полиномиальный код должен делиться на g(x), то для того, чтобы он был циклическим, многочлен a'(x) должен делиться на g(x). Из этого соображения можно сформулировать следующую теорему. Полиномиальный код является циклическим тогда и только тогда, когда многочлен g(x) является делителем многочлена xⁿ–1. В этом случае многочлен g(x) называется порождающим многочленом циклического кода.

В теории кодирования доказывается следующая теорема: если многочлен g(x) имеет степень n–k и является делителем xⁿ–1, то C(g(x)) является линейным циклическим (n, k)-кодом.

Многочлен xⁿ–1 разложим на множители xⁿ–1 = (x–1)(x^n-1+x^n-1+…+1). Следовательно, циклические коды существуют при любом n. Число циклических n-разрядных кодов равно числу делителей многочлена xⁿ–1. Для построения циклических кодов разработаны таблицы разложения многочленов xⁿ–1 на неприводимые многочлены, то есть на такие, которые делятся только на единицу и на самого себя.

Рассмотрим, например, какие коды можно построить на основе многочлена x⁷–1 над полем GF(2). Разложение многочлена на неприводимые множители имеет вид

Поскольку можно образовать шесть делителей многочлена x⁷–1, комбинируя неприводимые делители, существует шесть двоичных циклических кодов. (n, k)-код определяется, во-первых, значением n, а во-вторых, значением k = n – s, s – степень многочлена-делителя xⁿ–1, определяющего код. Ниже приведены делители полинома и соответствующие им значения k:

x – 1, s=1, k=6;

x³+x²+1, s=3, k=4;

x³+x+1, s=3, k=4;

(x–1)(x³+x²+1)=x⁴+x²+x+1, s=4, k=3;

(x–1)(x³+x+1)=x⁴+x³+x²+1, s=4, k=3;

(x³+x²+1)( x³+x+1)=x⁶+ x⁵+ x⁴+ x³+ x²+ x, s=6, k=1.

(7, 6)-код имеет лишь один проверочный символ, а (7, 1)-код – лишь один информационный. Они являются соответственно кодом с проверкой на чётность и кодом с повторением.

Как и обычный линейный код, циклический код может быть задан порождающей матрицей. Следовательно, задача состоит в том, чтобы найти такую матрицу, то есть найти k линейно независимых кодовых комбинаций, образующих её. Воспользуемся для этого свойством замкнутости циклического кода относительно операции циклического сдвига. Заметим, что циклический сдвиг вправо на один разряд эквивалентен умножению многочлена g(x) на x. Тогда порождающую матрицу можно построить, взяв в качестве строк порождающий многочлен и k его циклических сдвигов:

Например, рассмотрим один из делителей многочлена x⁷–1, а именно полином g(x)=1+x+x³. Ему соответствует кодовая комбинация 1101000 (выписаны коэффициенты при степенях 0, 1, …, 6 порождающего многочлена, так как кодовая комбинация содержит 7 символов). Тогда порождающая матрица (7,4) имеет вид

Рассмотрим теперь, как с помощью порождающего многочлена g(x) = 1+x+x³ осуществляется кодирование (7, 4)-кодом. Возьмём, например, 4-разрядное слово (0101), которому соответствует многочлен f(x) = x + x³. Перемножив эти два многочлена:

f(x)g(x) = (x+x³)(1+x+x³) = x+x²+x³+x⁶,

получим кодовую комбинацию 0111001. Аналогично можно получить кодовые слова для всех 4-разрядных двоичных слов. Однако получившийся код, как видно, не является разделимым, что неудобно для практических нужд.

Чтобы закодировать сообщение h(x) циклическим кодом C(g(x)), который является разделимым, нужно разделить многочлен x^n-kh(x) на g(x) и прибавит остаток от деления к многочлену x^n-kh(x).

Для примера рассмотрим кодовую комбинацию 1101. Этому вектору соответствует полином h(x)=1+x+x³. Тогда x^n-k h(x)=x³+x⁴+x⁶. Разделим получившийся многочлен на g(x) = 1+x+x³, получим остаток, равный 0. Тогда кодовый вектор равен 0001101.