Теория вероятности кр 1. ТерВер_Сем_1. Решение nколво всех возможных комбинаций N10 10 101000 M(A)колво комбинаций при условии, что цифры различны
 Скачать 32.99 Kb. Скачать 32.99 Kb.
|
|
Вариант 5. Задание 1. Шифр кодового замка состоит из 3-х цифр. Найти вероятность того, что все они различны; шифр заканчивается цифрой 7. Решение N-кол-во всех возможных комбинаций N=10  10 10 10=1000 10=1000M(A)-кол-во комбинаций при условии, что цифры различны M(A)=10  9 9 8=720 8=720По классическому определению: P(A)= 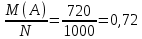 2. M(B)- кол-во комбинаций при условии, что последняя цифра 7 M(B)=10  10 10 1=100 1=100По классическому определению: P(B)= 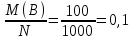 Ответ: а) P(A)=0,72; б) P(B)=0,1. Задание 2. Из 28 костей домино случайно выбирают две. Найти вероятность того, что из них можно составить цепочку согласно правилам игры. Решение: N- кол-во всех возможных комбинаций N= 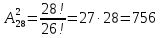 Теперь найдем кол-во благоприятных исходов M: Всего костей 28, из которых 7 являются «дублями», т.е оба числа на них одинаковые. Первая кость является «дублем». Тогда ей подходят 6 других костей с таким же числом. В этом случае кол-во комбинаций M1=7  6=42 6=42Первая кость не является «дублем». Тогда для каждого из двух чисел на этой кости подходит 6 других костей, т.е 12 вариантов. В этом случае кол-во комбинаций M2=(28-7)  12=21 12=21 12=252 12=252M=M1+M2=252+42=294 По классическому определению: P= 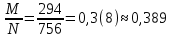 Ответ: Р 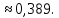 Задание 3. Стрелок произвел три выстрела по мишени. Событие Аk – попадание в мишень при k-ом выстреле (k=1,2,3). Выразить через А1, А2, А3 следующие события: А-хотя бы одно попадание; В-три промаха Решение: Событие А наступает тогда и только тогда, когда наступает или событие А1, или событие А2, или событие А3. Отсюда получаем, что А=А1+А2+А3. Событие 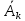 - промах при k-ом выстреле (k=1,2,3). Очевидно, что событие B наступает, только когда наступает и событие - промах при k-ом выстреле (k=1,2,3). Очевидно, что событие B наступает, только когда наступает и событие 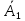 , и событие , и событие 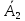 , и событие , и событие 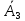 . .Отсюда получаем, что B= 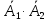 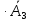 . .Ответ: А=А1+А2+А3 , B= 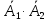 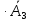 . .Задание 4. В собираемый механизм входят две одинаковые шестерни. Технические условия нарушаются, если обе они оказываются с отклонениями по толщине зуба в положительную сторону от среднего размера(заедание). У сборщика имеется 10 шестерен, из которых 3 с плюсовым отклонением. Определить вероятность нарушения технических условий при случайном выборе двух шестерен. Решение: Найдем общее число исходов N: N= 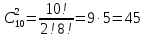 Теперь найдем число изходов, при которых будут взяты 2 шестерни с отклонениями. M= 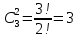 По классическому определению: P= 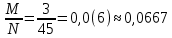 Ответ: Р 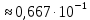 Задание 5. Среди облигаций займа половина выигрышных. Сколько облигаций следует взять, чтобы рассчитывать на выигрыш с вероятностью большей 0,95? Решение: Пусть m- количество купленных облигаций А – выигрыш хотя бы одной из m 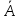 - все х облигаций проигрышные - все х облигаций проигрышные Тогда, P(A)=1-P( 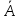 ). ).Найдем P( 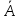 ) по формуле Бернули: ) по формуле Бернули:n - всего облигаций m - кол-во проигрышных облигаций p = 0,5 – вероятность выигрыша одной облигации q = 1-0,5=0,5 – вероятность проигрыша одной облигации В нашем случае n=m. Получим, P( 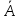 )= )= 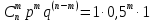 = =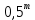 Тогда, 1- 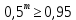  - -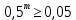  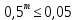 Прологарифмируем: m 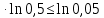 Т.к 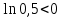 - меняем знак неравенства. - меняем знак неравенства.m 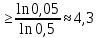 Т.к m – целое число облигаций, округляем в большую сторону. Ответ: m 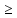 5. 5.Задача 6. Два стрелка независимо один от другого стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8 , для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок. Решение: H1 – оба стрелка не попали по мишени; H2 – попал первый стрелок; H3 – попал второй стрелок; H4 – оба стрелка попали по мишени. Найдем вероятности этих гипотез: Р(H1) = 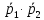 = 0,2 = 0,2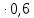 = 0,12; = 0,12;Р(H2) = 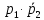 = 0,8 = 0,8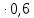 = 0,48; = 0,48;Р(H3) = 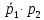 = 0,2 = 0,2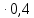 = 0,08; = 0,08;Р(H4) = 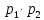 = 0,8 = 0,8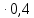 = 0,32; = 0,32;Найдем для этих гипотез условные вероятности события А – один из стрелков попал по мишени: P(A/ H1) = 0; P(A/ H2) = 1; P(A/ H3) = 1; P(A/ H4) = 0; Найдем вероятность события А: P(A)=0,12  0+0,48 0+0,48 1+0,08 1+0,08 1+0,32 1+0,32 0=0,56 0=0,56P(H2/A) = 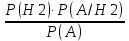 = =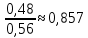 Ответ: P(H2/A) 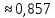 Задание 7. За одну смену первый рабочий производит 60 изделий с вероятностью брака 5%, а второй рабочий 70 изделий с вероятностью брака 4%. Найти наивероятнейшие числа качественных изделий, изготовленных каждым рабочим за смену. Решение: K1 - наивероятнейшие число качественных изделий, изготовленных первым рабочим за смену; K2 - наивероятнейшие число качественных изделий, изготовленных вторым рабочим за смену. Наивероятнейшее число можно найти из неравенсва: 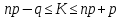 Подставим наши значения: 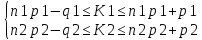 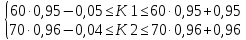 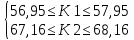 Ответ: K1 = 57 изделий, K2 = 68 изделий. |
