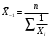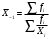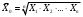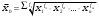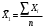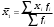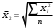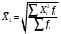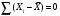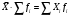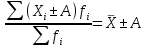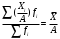13-16 Стата. 13. Представление статистических данных в таблицах, графиках, картограммах. Правила оформления статистических таблиц и графиков
 Скачать 268.08 Kb. Скачать 268.08 Kb.
|
|
13. Представление статистических данных в таблицах, графиках, картограммах. Правила оформления статистических таблиц и графиков. Статистическая таблица – способ представления статистических данных с помощью строк и столбцов. Строки статистической таблицы образуют подлежащее (исследуемый объект), столбцы – сказуемое (показатели, характеризующие объект). Важным атрибутом таблицы является заголовок, который отражает её общее содержание. Статистический график – это чертёж, на котором статистические данные описываются с помощью геометрических образов и/или знаков. Описание статистического графика включает в себя заголовок, единицы измерения, условные обозначения (легенду). В масштабные характеристики статистического графика входят масштаб, масштабные шкалы и масштабные знаки. Картограммой считается графическое изображение статистических данных, сведенных по географическому принципу (напр., по административному делению), представляющее собой географическую карту, территории, которые окрашены (или заштрихованы) в соответствии с величиной исследуемого показателя, наблюдаемой на данной территории. Наглядное представление результатов статистического исследования обеспечивается средствами визуализации данных: графиков, диаграмм, структурных схем, таблиц, рисунков, карт и т.д. Рекомендуется соблюдать основные правила использования этих методов представления информации. Например, требования к составлению и оформлению таблиц: - название таблицы включает задачи представленной информации, территориальные границы, период или момент времени, к которому относится изучаемая совокупность, единицы измерения, если они одинаковы для всех данных таблицы; - многозначные числа следует округлять в пределах одной графы с одинаковой степенью точности; - если единицы измерения неодинаковы, то в верхних или боковых заголовках обязательно следует указывать, в каких единицах приводятся статистические данные – в тоннах, в штуках, в рублях и пр.; - желательно давать нумерацию граф. - заголовки граф следует сформулировать так, чтобы были ясны смысл данной величины и порядок ее расчета; - объекты изучения, признаки и показатели должны быть расположены в логическом порядке с учетом необходимости рассматривать их совместно. - не должно быть пустых клеток: знак тире (-) – когда явление отсутствует; х – если явление не имеет осмысленного содержания; многоточие (…) – когда отсутствуют сведения о его размере (или делается запись "Нет сведений"). Если сведения имеются, то числовое значение меньше принятой в таблице точности оно выражается дробным числом (0,0). 14. Сущность и значение средних величин. Виды и формы средних, основные правила построения средних величин. Свойство мажорантности средних величин. Средняя величина - обобщающая типическая характеристика изучаемого явления, рассчитанная по одному количественному признаку, в которой погашается вариация (различие) индивидуальных значений изучаемого признака разных единиц совокупности. Основная задача средних величин дать характеристику достигнутого уровня развития изучаемого явления в соответствующих условиях места и времени. Различают две формы средних величин: простую и взвешенную. Простая средняя ( 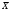 ) считается по первичным признакам, выраженным абсолютной величиной: ) считается по первичным признакам, выраженным абсолютной величиной: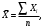 где Хi - значение осредняемого первичного признака по каждой единице совокупности; n - число единиц совокупности. Во взвешенной средней величине наряду с осредняемым признаком используется признак – вес, один или более. Взвешенная средняя может определяться двумя способами: а) как отношение двух итоговых подсчётов по первичным признакам, определяющим значение вторичного признака; б) на основе отдельных значений осредняемого вторичного признака и признака - веса. 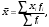 где: Хi - значение осредняемого вторичного признака по каждой единице совокупности; fi - признак – вес; fi - сумма весов. Виды и формы средних величин
Доказано, что если рассчитывать по одним и тем же данным средние разных видов, то их значения будут различны: чем выше знак степени средней, тем больше значение средней величины. Это свойство называется свойством мажорантности (преобладания), и используется для логического контроля правильности расчёта разных форм средних. 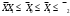 15. Формы средней арифметической и средней гармонической. Особенности их применения в статистике. Привести примеры. Виды и формы средних величин
Они часто применяются для осреднения относительных величин интенсивности, т.е. показателей, имеющих дробную размерность. При этом соблюдаются следующие правила. Если имеются дополнительные данные по числителю дробной размерности, то применяется средняя гармоническая. Если имеются дополнительные данные по знаменателю дробной размерности, то применяется средняя арифметическая. Если неясно, к числителю или знаменателю относятся дополнительные данные, то поочередно применяются средняя гармоническая и арифметическая, а затем определяется средняя между ними величина. В социально-экономической статистике, в частности в статистике туризма, особое значение придается расчету средних величин. Пример. Вычислить желаемый размер заработной платы, 50 сотрудников офиса. 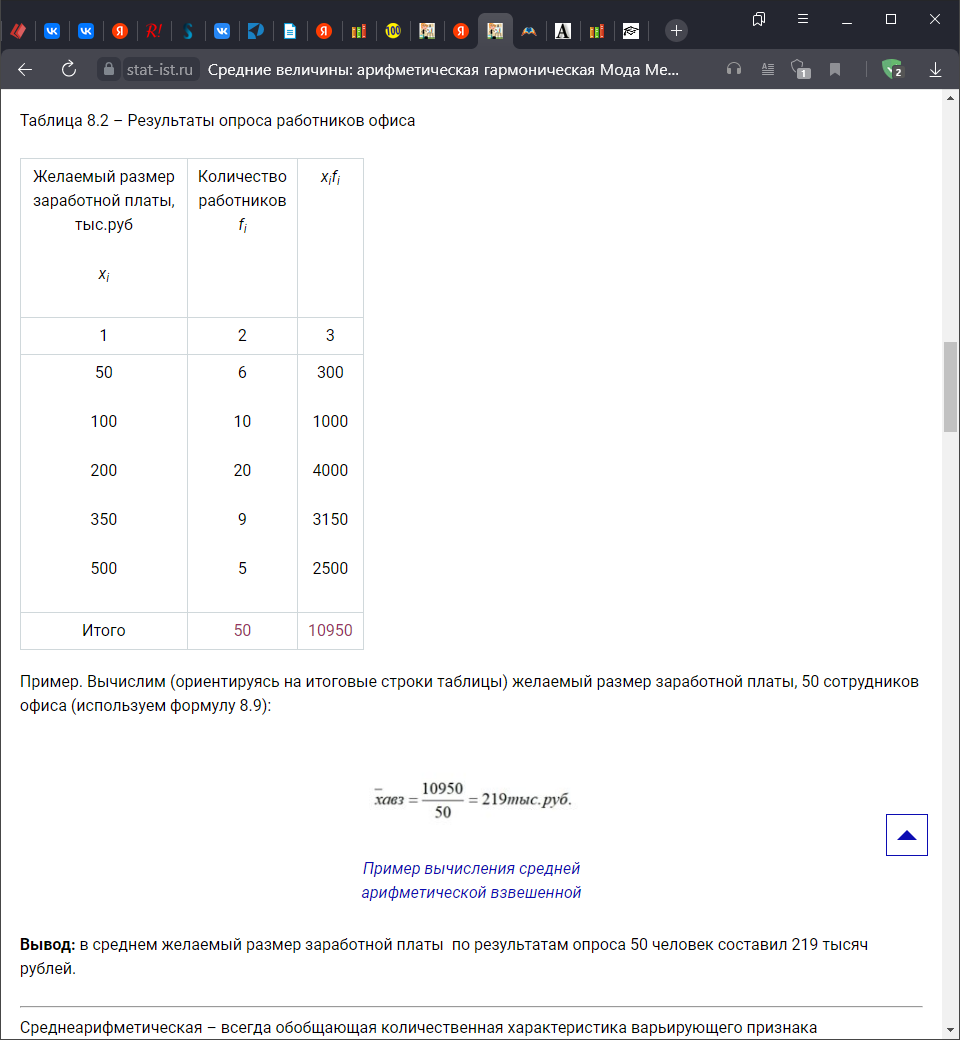 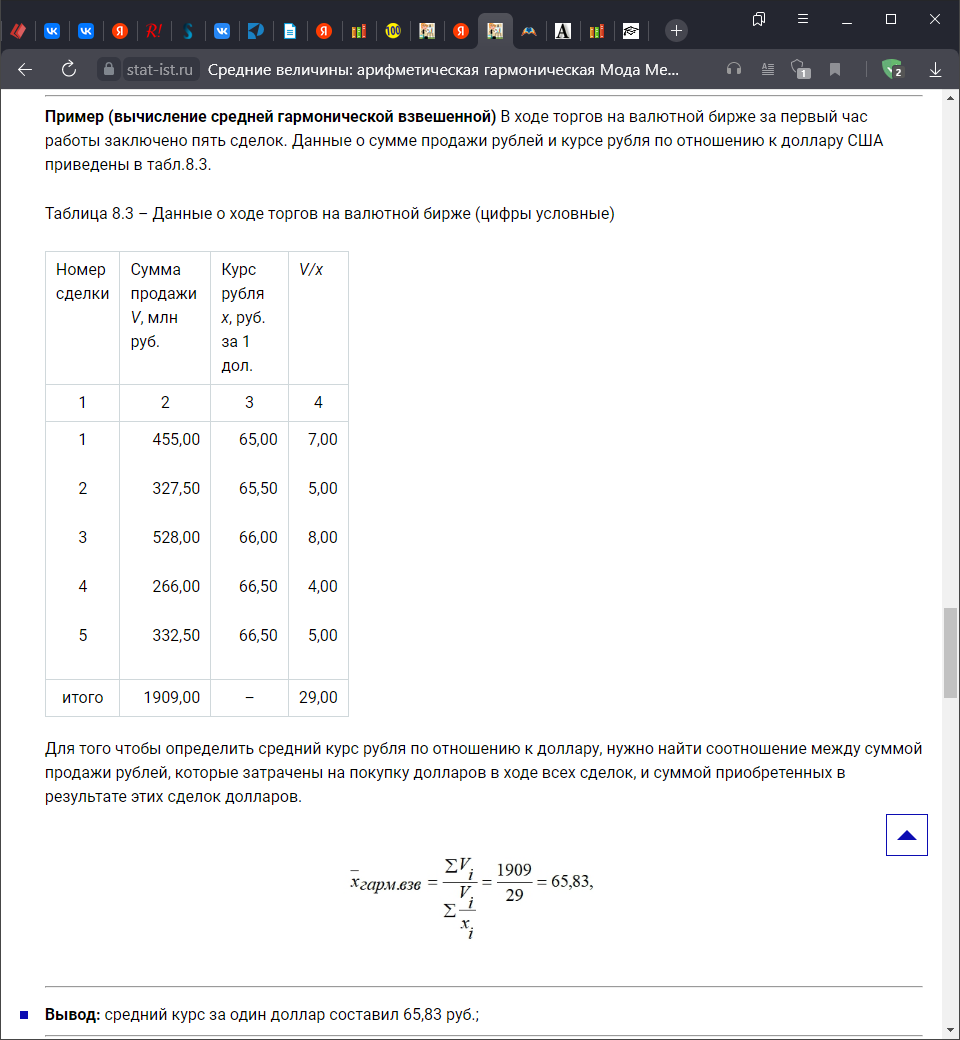 16. Свойства средней арифметической (учебник). Свойства средней арифметической
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||