Лекция+15_КРИВОЛИНЕЙНЫЕ+ИНТЕГРАЛЫ. 15. 1 Криволинейный интеграл I рода
 Скачать 495.5 Kb.
|
|
ЛЕКЦИЯ 15. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ Если понятие определенного интеграла обобщить на случай, когда областью интегрирования является некоторая кривая, то такой интеграл называется криволинейным. 15.1 Криволинейный интеграл I рода Пусть функция 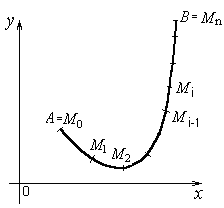 задана вдоль непрерывной кривой  на плоскости  . Разобьем кривую произвольно на  частей (рис.80) точками . Рисунок 80 Обозначим через  длину дуги  ,  - наибольшую из длин частичных дуг (т.е.  ). Выберем на каждой дуге произвольную точку  и составим сумму . (15.1)Сумма (15.1) называется интегральной суммой для функции по кривой .Если существует конечный предел интегральных сумм (15.1) при  , не зависящий ни от способа разбиений кривой, ни от выбора точек в них, то этот предел называется криволинейным интегралом первого рода от функции по кривой и обозначается или  .Тогда, по определению имеем = . (15.2)Теорема. Если функция непрерывна в каждой точке гладкой кривой, то криволинейный интеграл первого рода существует.15.2 Основные свойства криволинейного интеграла I рода
 .
15.3 Вычисление криволинейного интеграла I рода Для вычисления криволинейного интеграла I рода используют одну из следующих формул:
 ; (15.3)
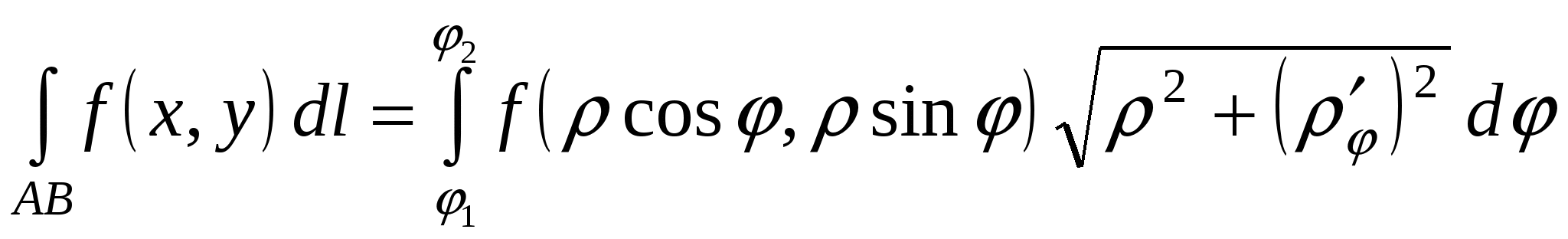 ; (15.4)
 . (15.5)Замечание. Криволинейный интеграл первого рода от непрерывной в некоторой пространственной области функции  по длине дуги определяется аналогично, т.е. =, где .Если кривая  задана параметрическими уравнениями  ,  ,  ,  , то . (15.6)Пример 15.1. Вычислить интеграл  , где - отрезок прямой, заключенный между точками  и  .Решение. Найдем уравнение прямой :  .При движении от точки  к точке   меняется от 0 до 1. По формуле (15.3) имеем: Пример 15.2. Вычислить интеграл  , где - арка циклоиды  ,  , причем  .Решение. Так как  ,то по формуле (15.4) имеем   Пример 15.3. Вычислить интеграл , где - контур окружности  .Решение. Перейдем к полярным координатам по формулам перехода  ,  .Тогда уравнение данной окружности примет вид  , .Угол 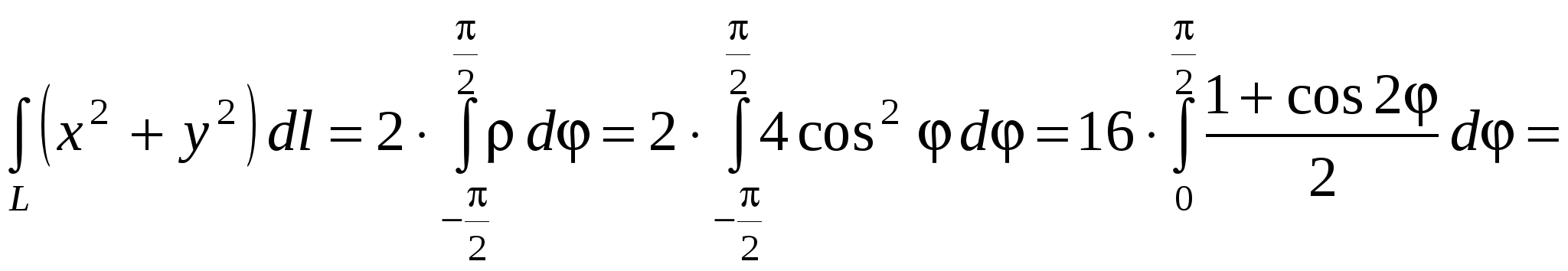 меняется от  до  , т.к. окружность расположена в I и IV четвертях. По формуле (15.5) имеем  15.4 Некоторые приложения криволинейного интеграла I рода 1) Длина кривой Длина  кривой вычисляется по формуле . (15.7)2) Площадь цилиндрической поверхности Если образующая поверхность параллельна оси  и ее направляющей является кривая , лежащая в плоскости  , то площадь поверхности, задаваемой функцией  , находится по формуле .3) Масса кривой Если материальная кривая имеет плотность  в точке , то её масса вычисляется по формуле .4) Статические моменты, центр тяжести Статические моменты относительно осей  и  соответственно равны , ,а координаты центра тяжести вычисляются по формулам: 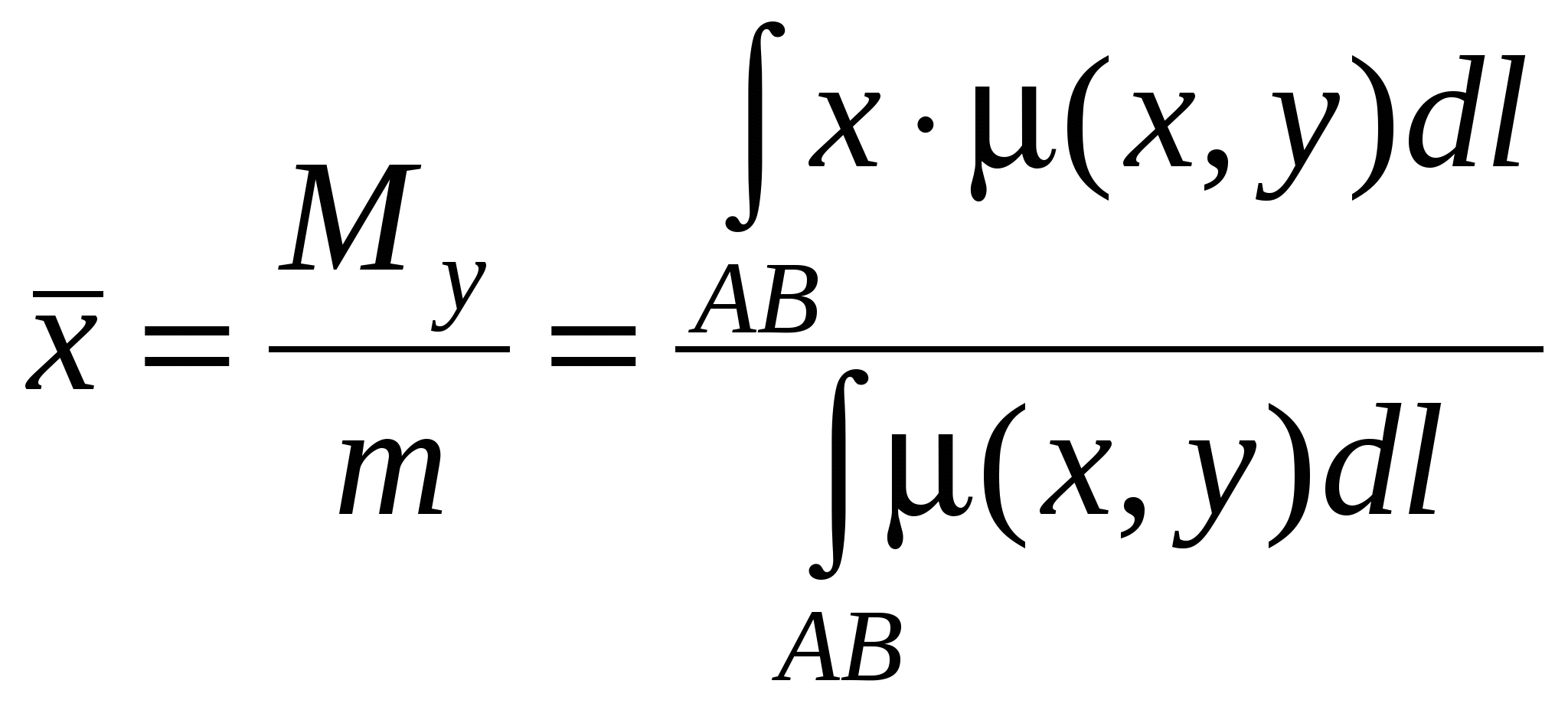 ,  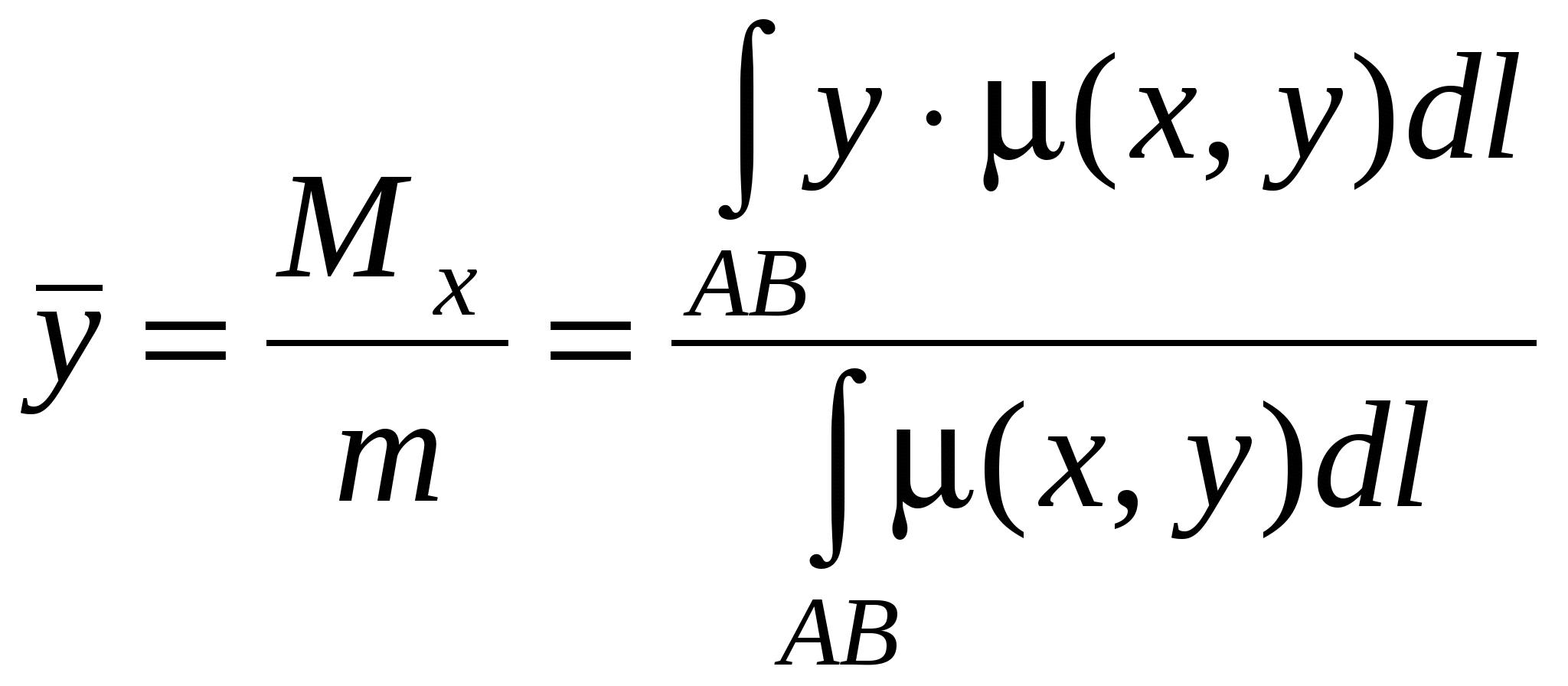.5) Моменты инерции Моменты инерции  ,  ,  материальной кривой относительно осей и , начала координат  соответственно равны , , .Пример 15.4. Найти координаты центра тяжести однородной дуги циклоиды 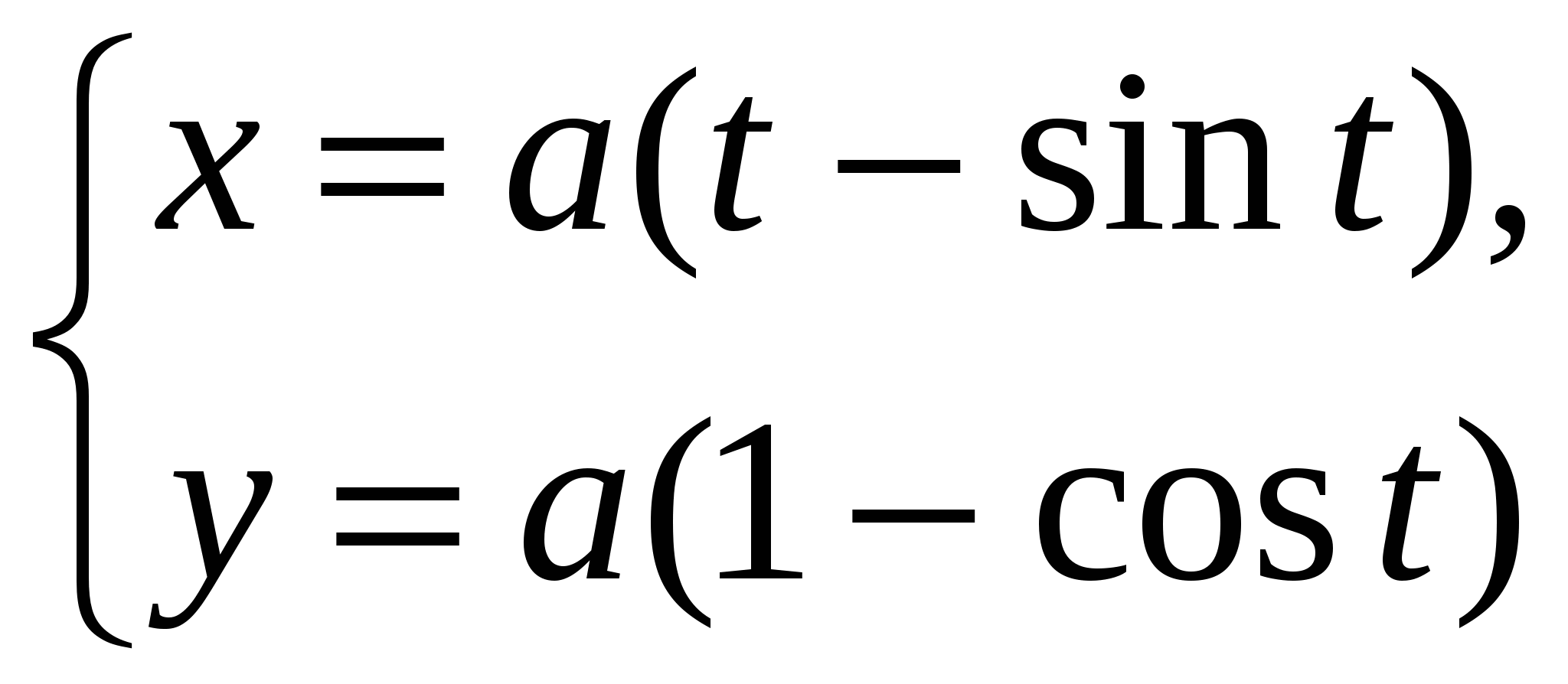 если  (рис.81).П  лотность считать равной единице в каждой точке кривой (  ).Рисунок 81 Решение. Учитывая симметрию кривой относительно прямой  , получаем абсциссу центра тяжести:  .Найдем сначала массу кривой   .Тогда 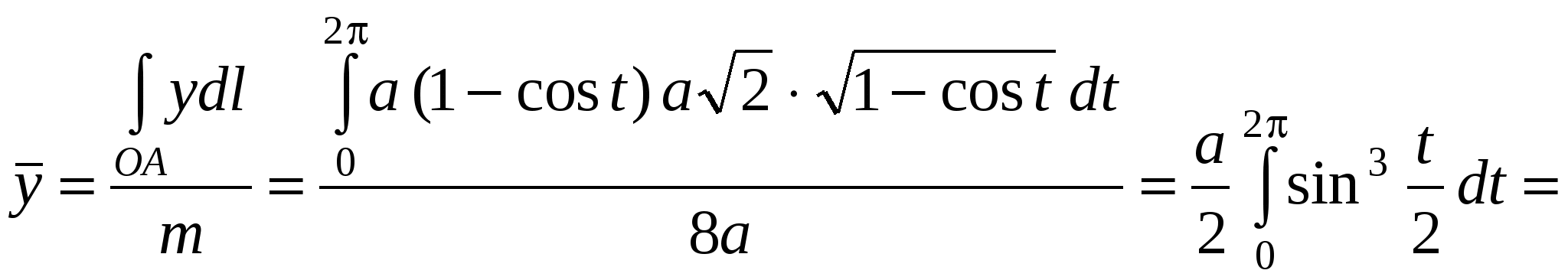 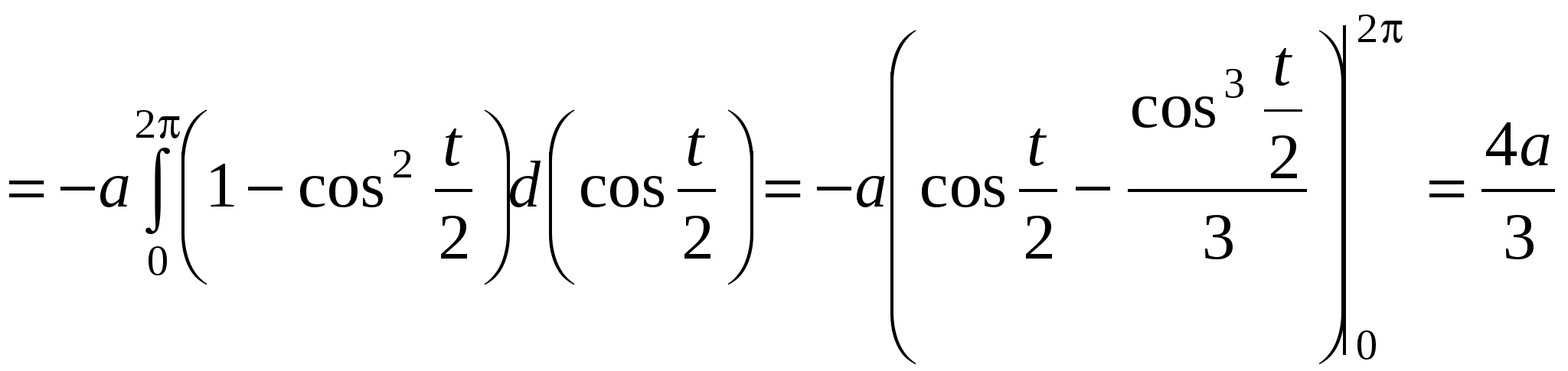 .Итак, искомый центр тяжести дуги – точка  .15.5 Криволинейный интеграл II рода Пусть на кривой в плоскости определены две ограниченные функции  и  . Разобьём кривую на частей точками: .Обозначим проекции вектора 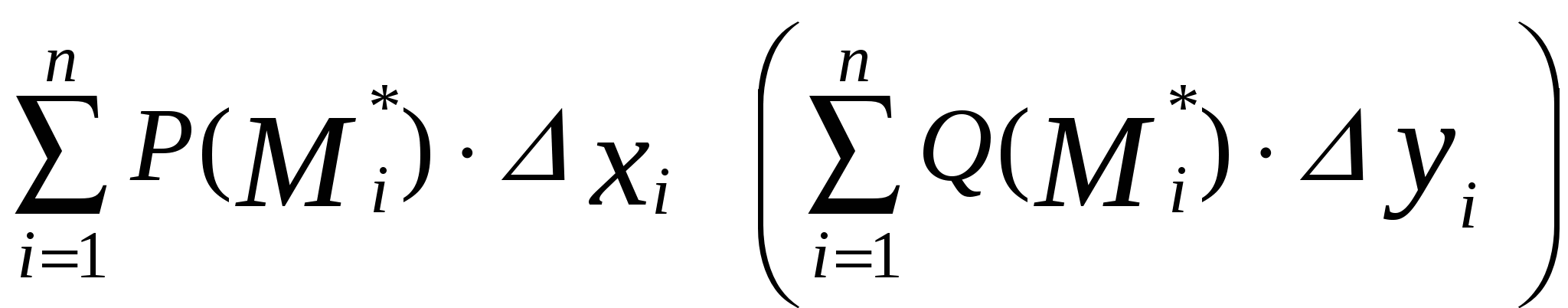 на оси координат через  и  . На каждой частичной дуге  возьмем произвольную точку  и составим сумму для функций и : . (15.8)Сумма (15.8) называется интегральной суммой для функции по переменной  (для функции по переменной  ).Введем обозначения:  - длина дуги , .Если существует конечный предел интегральных сумм (15.8) при  , не зависящий ни от способа разбиения кривой на части, ни от выбора точек в них, то его называют криволинейным интегралом второго рода от функции () по кривой и обозначают .Обычно рассматривают сумму интегралов по координате и по координате : . (15.9)Интеграл (15.9) называют общим криволинейным интегралом второго рода. Теорема. Если функции и непрерывны на гладкой кривой , то криволинейный интеграл существует.Криволинейные интегралы второго рода обладают теми же свойствами, что и криволинейные интегралы первого рода, только они зависят от выбора направления кривой (от  к  или от к ): если изменить направление обхода, то интеграл меняет знак, т.е. .Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления обхода кривой. Условимся называть направление положительным, если область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Криволинейный интеграл по замкнутому контуру , пробегаемому в положительном направлении, часто обозначают символом .15.6 Вычисление криволинейного интеграла II рода Криволинейные интегралы второго рода сводятся к определенным интегралам. Для вычисления криволинейного интеграла второго рода пользуются одной из следующих формул: а) если кривая задана уравнением  и при перемещении из точки в точку меняется от  до  , то . (15.10)б) если кривая задана параметрическими уравнениями  ,  и при перемещении из точки в точку параметр  меняется от  до  , то . (15.11)Аналогично определяется криволинейный интеграл от непрерывных функций в некоторой пространственной области функций  и  по координатам вдоль дуги пространственной кусочно-гладкой кривой , расположенной в этой области: .Если кривая задана параметрическими уравнениями , ,   , то  .Замечание. Криволинейные интегралы первого и второго рода связаны соотношением:  ,где и 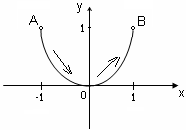- углы, образованные касательной к кривой в точке с осями и соответственно.П  ример 15.5. Вычислить  , где - дуга параболы  , пробегаемая от точки  до точки  (рис.82).Рисунок 82 Так как при движении из точки 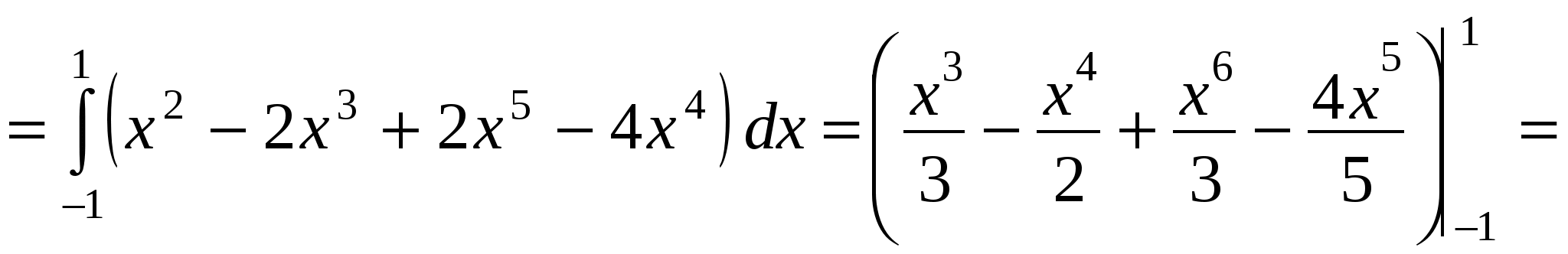в точку меняется от  до  , то по формуле (6.1) имеем   .15.7 Формула Грина Между двойным интегралом по области  и криволинейным интегралом по границе этой области существует связь, определяемая формулой Грина.Пусть - кусочно-гладкий контур на плоскости , а - ограниченная этим контуром замкнутая область.Теорема. Если функции и непрерывны в области и имеют в этой области непрерывные частные производные, то справедлива формула . (15.12)Формула (15.12) называется формулой Грина. Пример 15.6. С помощью формулы Грина вычислить криволинейный интеграл  ,где - к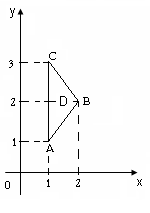онтур треугольника с вершинами в точках  ,  и  (рис.83).Р  исунок 83 Решение. Применим формулу Грина (7.1). В данном случае  ,  , поэтому ,  .Тогда получаем    .15.8 Условия независимости криволинейного интеграла II рода от пути интегрирования Плоская область называется односвязной, если для любого замкнутого контура , лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области .Теорема. Для того, чтобы криволинейный интеграл  не зависел от пути интегрирования в односвязной области , в которой функции и непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие . (15.13)Если выполнено условие (15.13) и - замкнутый контур, то . (15.14)Если выполнено условие (15.13), то выражение  является полным дифференциалом некоторой функции, определенной в области , т.е. .Пример 15.7. Вычислить интеграл  , где - окружность  .Решение. Здесь  ,  . Получаем .Так как условие (15.13) выполняется и контур замкнутый, тогда по формуле (15.14) данный интеграл равен нулю.15.9 Некоторые приложения криволинейного интеграла II рода 1) Площадь плоской области Площадь  плоской области , расположенной в плоскости и ограниченной замкнутой линией , находится по формуле , (15.15)где направление обхода контура выбрано так, что область все время слева от пути интегрирования.2) Работа силы Работа, совершаемая переменной силой  вдоль кривой , находится по формуле . (15.16)Пример 15.8. Вычислить работу силы  при перемещении материальной точки по прямой  из точки в точку  .Решение. Из формулы (15.16) следует, что  . |
, т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования.
.
, где 
.
, где кривая 
и 
.
для всех точек кривой 
, где точка 
лежит на кривой 
, 
, то
и 
- непрерывно дифференцируемые функции по 
, 
, то