15_ТВ_и МС. 15. Нормальное распределение. Правило трех сигм Правило двух сигм
 Скачать 92.7 Kb.
|
 15. Нормальное распределение. Правило трех сигм  Правило двух сигм  Правило одной сигмы  Умения Алгоритм действий Нормальное распределение. Правило трех сигм Правило двух сигм Правило одной сигмы 1. Определяются значение параметров  и  нормального распределения.2.Значения  и подставляют в формулу  3.Значения  и  берутся из таблицы нормального распределения.4.Подсчитывается вероятности с помощью правил трех сигм , двух сигм и одной сигмы. Задание 15. Случайная величина  имеет нормальное распределение ;- среднеквадратическое отклонение  . Найти  Решение № п/п Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму 1 Записывается  .  2 Вычисляется 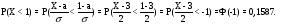  3 Вычисляется   4 Вычисляется  с помощью правила одной «сигмы». 5 Вычисляется 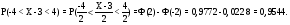 с помощью правила двух «сигм». 6 Вычисляется 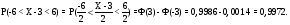 с помощью правила трех «сигм». 16. Неравенство Чебышева  Умения Алгоритм действий Неравенство Чебышева 1.Определяются  , ,.2.Значения. , , а подставляются в неравенство Чебышева.Задание 16. Все мужчины – случайная величина со средним 80 кг и дисперсией 50 кг2. Оценить с помощью неравенства Чебышева вероятность того, что вес случайно встреченного мужчины отличается от среднего на величину большую 10 кг. Решение  № п/п Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму 1 Записываются   2 Подставляются значения в неравенство Чебышева Из неравенства Чебышева следует  17. Предельная формула Пуассона для последовательности независимых испытаний Бернулли. Умения Алгоритм действий Предельная формула Пуассона для последовательности независимых испытаний Бернулли. 1. Подсчитывается значение =пр. При действует формула Пуассона: Задание 17. Вероятность детали быть бракованной равна 0, 01. Произведено 300 деталей. Какова вероятность того, что в этой партии точно 4 бракованные детали? Более 4? Решение № п/п Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму 1 Вычисляется произведение   2 Подставляется значение 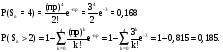 в формулу Пуассона и подсчитывается   18. Предельная интегральная теорема Муавра-Лапласа для последовательности независимых испытаний Бернулли. Умения Алгоритм действий Предельная интегральная теорема Муавра-Лапласа для последовательности независимых испытаний Бернулли. 1.Подсчитывается значение =пр. При действует формула Муавра-Лапласа 2.Значения  и  находятся из таблиц нормального распределения.Задание 18. Игральную кость бросают 600 раз. Какова вероятность того, что число выпадений шестерки будет между 90 и 105? Решение № п/п Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму 1 Вычисляется произведение   .2 Вычисляется значение   .3 Вычисляются значения  . 4 Значения  берутся из таблицы нормального распределения. |