им C.Cейфуллин КазАТУ. 16-дәріс. 5-кредит Жоғ. мат.2. 16дріс. Ытималдытар теориясы Е болмаса бір оианы пайда болу ытималдыы
 Скачать 114.85 Kb. Скачать 114.85 Kb.
|
|
16-дәріс. Ықтималдықтар теориясы Ең болмаса бір оқиғаның пайда болу ықтималдығы. Өзара үйлесімсіз 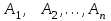 оқиғаларының ең болмаса біреуі пайда болуы А оқиғасының ықтималдығы оқиғаларының ең болмаса біреуі пайда болуы А оқиғасының ықтималдығы  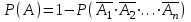 формуласымен анықталады, мұндағы 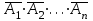 оқиғасы берілген оқиғалардың барлығының да пайда болмау оқиғасы. оқиғасы берілген оқиғалардың барлығының да пайда болмау оқиғасы.Егер 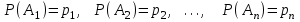 және және 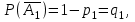 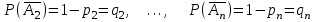 болса, онда болса, онда 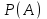 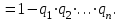 Егер 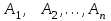 , оқиғаларының ықтималдықтары р-ға тең болса, онда ең болмаса біреуінің пайда болу А оқиғасының ықтималдығы , оқиғаларының ықтималдықтары р-ға тең болса, онда ең болмаса біреуінің пайда болу А оқиғасының ықтималдығы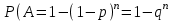 формуласымен анықталады. Е с к е р т у. Тәжірибе кезінде А және В оқиғаларының ең болмаса біреуінің пайда болу оқиғасының ықтималдығын әр түрлі формуламен табуға болады: 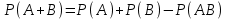 немесе 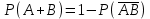 немесе немесе 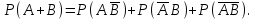 2-мысал. Үш атқыш нысанаға бір-бірден оқ атады. Бірінші атқыштың нысанаға тию ықтималдығы 0,7-ге; екіншісі үшін – 0,8-ге; үшіншісі үшін - 0,9-ге тең. Нысанаға а) үшеуінің де тию; ә) тек екеуінің тию; б) тек біреуінің тию; в) үшеуінің де тимеу; г) ең болмаса біреуінің тию оқиғасының ықтималдығын табу керек. Шешуі. Бірінші атқыштың нысанаға тигізу оқиғасын А1, ал екіншісін А2, үшіншісін А3 деп белгілейік. Бұл оқиғалардың тимеу ықтималдықтарын табайық: 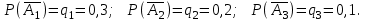 а) В1 оқиғасы– «үшеуінің де нысанаға тиюі», онда 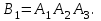 Осыдан Осыдан 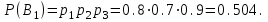 ә) В2 оқиғасы – «тек екеуінің нысанаға тиюі». Онда 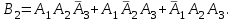 Осыдан Осыдан 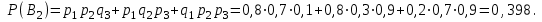 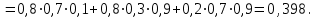 б) В3 оқиғасы – «тек біреуінің нысанаға тиюі». Онда 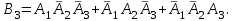 Осыдан Осыдан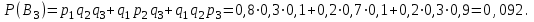 в) В4 оқиғасы – «үшеуінің де нысанаға тимеуі». Онда 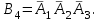 Осыдан Осыдан 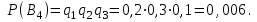 г) В5 оқиғасы – «ең болмаса біреуінің нысанаға тиюі». Онда В5 оқиғасы мен В4 оқиғасы толық топ құрайды. Осыдан 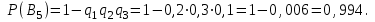 2-мысал. Мергеннің бір рет атқанда нысанаға тигізу ықтималдығы 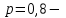 ге тең. Төрт рет атқанда, ең болмаса бір рет тигізу оқиғасының ықтималдығын табу керек. ге тең. Төрт рет атқанда, ең болмаса бір рет тигізу оқиғасының ықтималдығын табу керек.Шешуі. Нысанаға тимеу ықтималдығы 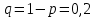 болғандықтан болғандықтан 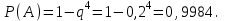 Толық ықтималдық формуласы. Бейес формуласы Егер А оқиғасы өзара үйлесімсіз, толық топ құрайтын В1,В2,...,Вn оқиғаларының біреуімен бірге пайда болса, онда А оқиғасының ықтималдығы 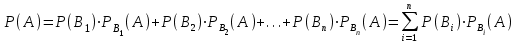 толықықтималдықформуласымен анықталады, мұндағы толықықтималдықформуласымен анықталады, мұндағы 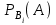 - шартты ықтималдықтар. - шартты ықтималдықтар. 3-мысал. Үш атқыштың нысанаға тигізу ықтималдығы сәйкесінше 0,6; 0,7; 0,8 тең. Алдымен бір атқыш таңдап алынған. Ол нысанаға атқанда оқтың тию ықтималдығын табу керек. Шешуі. А – оқтың нысанаға тию оқиғасы, Ві – і-ші атқышты таңдап алу оқиғасы, і=1,2,3. Атқышты таңдап алу оқиғасы “тең мүмкіндікті” оқиға болғандықтан 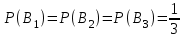 және және 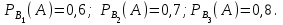 Олай болса, 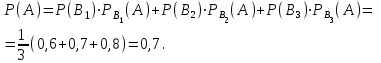 4-мысал. №1-ші 5 жәшікте 3 ақ және 7 қара; №2-ші 7 жәшікте 2 ақ және 8 қара; №3-ші 3 жәшікте 4 ақ және 6 қара шар бар. Алдымен кез келген жәшік алынып, содан кейін одан бір шар алынды. Осы шардың ақ болу ықтималдығын табу керек. Шешуі. А – шардың ақ болу оқиғасы, Ві – і-ші жәшіктен алу оқиғасы, і=1,2,3. барлық жәшіктің саны 15. 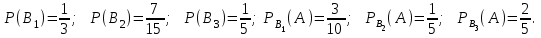 Осыдан 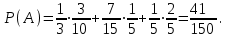 А оқиғасы өзара үйлесімсіз, толық топ құрайтын В1, В2,...,Вn оқиғаларының біреуімен бірге пайда болсын. Тәжірибе нәтижесінде А оқиғасы пайда болсын. Бұл жағдайда А оқиғасы пайда болғаннан кейінгі В1, В2,...,Вn оқиғаларының ықтималдықтары 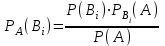 Бейесформуласымен анықталады. 5-мысал. Қоймадағы бөлшектердің 70% І зауыттан, оның 2% жарамсыз; 30 %-і ІІ зауыттан, оның 5% жарамсыз. Қоймадан алынған бір бөлшек жарамсыз болсын. Оның бірінші зауытта дайындалған болу ықтималдығын табу керек. Шешуі. А – қоймадан алынған бөлшек жарамсыз болу оқиғасы, В1 – І зауыттан, ал В2 – ІІ зауыттан шыққан бөлшек болу оқиғалары. 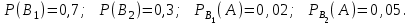 Осыдан 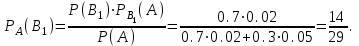 6-мысал. Топта 10 шаңғышы, 8 велосипедші, 6 желаяқтар бар. Квалификациялық нормасын орындау ықтималдығы шаңғышы үшін - 0,8; велосипедші үшін – 0,9; желаяқ үшін - 0,7-ге тең. Таңдап алынған спортшының квалификациялық норманы орындады. Осы спортшының шаңғышы болу ықтималдығын тап. Шешуі. А1 оқиғасы – «таңдап алынған спортшының квалификациялық норманы орындауы». В1 оқиғасы – «спортшының шаңғышы болуы», В2 оқиғасы – «спортшының велосипедші болуы», В3 оқиғасы – «спортшының желаяқ болуы». Онда 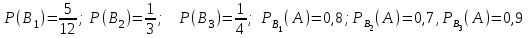 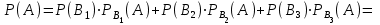 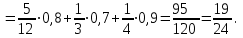 Осыдан спортшының шаңғышы болу ықтималдығы Бейес формуласымен есетеледі, яғни 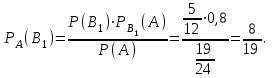 Жаттығулар 1. Ойын сүйегі бір рет лақтырылады. “1” цифрының пайда болмау ықтималдығын табу керек. Жауабы: 5/6. 2. Студент 60 сұрақтың 50-ін біледі. Алынған билет сұрақтарының (үш сұрағы бар) ең болмаса біреуін білетіндігінің ықтималдығын табу керек. Жауабы: 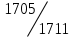 . .3. Жәшікте 4 қызыл, 6 ақ шар бар. Кездейсоқ 3 шар алынды. Алынған шарлардың ең болмаса біреуі ақ шар болу ықтималдығын табу керек. Жауабы: 29/30. 4. Атқыштың нысанаға бір рет атқандағы тигізу ықтималдығы 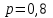 -ге тең. Атқыш 3 рет атқанда үшеуінің де нысанаға тию ықтималдығын табу керек. Жауабы: 0,512. -ге тең. Атқыш 3 рет атқанда үшеуінің де нысанаға тию ықтималдығын табу керек. Жауабы: 0,512.5. Үш ойын сүйегін лақтырғанда “6” цифрының ең болмаса бір рет пайда болу ықтималдығын табу керек. Жауабы: 91/216. 6. Атқыштың үш рет атқандағы нысанаға ең болмаса бір рет тигізу ықтималдығы 0,936 тең. Атқыштың бір рет атқандағы нысанаға тигізу ықтималдығын табу керек. Жауабы: 0,6. 7. Кітапханада 20 оқулық бар, оның жетеуі түптелген. Кітапханашы кез келген екі оқулық алды. Оқулықтардың түптелген болуының ықтималдығын табу керек. Жауабы: 21/190. 8. 100 лотерея билетінің 20-ы ұтыс билеттер. Алынған екі билеттің екеуінің де ұтыс билеттері болу ықтималдығын табу керек. Жауабы: 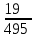 . .9. Екі атқыштың нысанаға тигізу ықтималдығы сәйкесінше 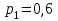 және және 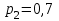 -ға тең. Олар нысанаға бір-бірден оқ атты. Келесі оқиғалардың ықтималдықтарын табу керек: а) екеуінің де нысанаға тигізуі; ә) тек біреуінің нысанаға тигізуі; б) екеуінің де нысанаға тигізе алмауы; в) ең болмаса біреуінің нысанаға тигізуі; г) ең болмаса біреуінің нысанаға тимеуі. Жауабы: а)0,42; ә)0,46; б) 0,12; в) 0,88; г) 0,58. -ға тең. Олар нысанаға бір-бірден оқ атты. Келесі оқиғалардың ықтималдықтарын табу керек: а) екеуінің де нысанаға тигізуі; ә) тек біреуінің нысанаға тигізуі; б) екеуінің де нысанаға тигізе алмауы; в) ең болмаса біреуінің нысанаға тигізуі; г) ең болмаса біреуінің нысанаға тимеуі. Жауабы: а)0,42; ә)0,46; б) 0,12; в) 0,88; г) 0,58.10. Атқыш нысанаға екі рет оқ атты. Оның нысанаға тигізу ықтималдығы 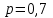 . Келесі оқиғалардың ықтималдығын табу керек: а) нысанаға екі рет тигізуі; ә) нысанаға тек бір рет тигізуі; б) нысанаға екі рет тигізе алмауы; в) нысанаға ең болмаса бір рет тигізуі; г) нысанаға ең болмаса бір рет тигізбеуі. . Келесі оқиғалардың ықтималдығын табу керек: а) нысанаға екі рет тигізуі; ә) нысанаға тек бір рет тигізуі; б) нысанаға екі рет тигізе алмауы; в) нысанаға ең болмаса бір рет тигізуі; г) нысанаға ең болмаса бір рет тигізбеуі. Жауабы: а)0,49; ә)0,42; б) 0,09; в) 0,91; г) 0,51. 11. Үш атқыш бір-бірінен тәуелсіз нысанаға бір-бірден оқ атқан. Олардың нысанаға тигізу ықтималдықтары: 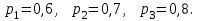 Келесі оқиғалардың ықтималдықтарын есептеу керек: а) барлық атқыштың нысанаға тигізуі; ә) атқыштың тек біреуінің тигізуі; б) атқыштың тек екеуінің тигізуі;в) атқыштың бәрінің нысанаға тигізбеуі; г) ең болмаса біреуінің нысанаға тигізбеуі. Келесі оқиғалардың ықтималдықтарын есептеу керек: а) барлық атқыштың нысанаға тигізуі; ә) атқыштың тек біреуінің тигізуі; б) атқыштың тек екеуінің тигізуі;в) атқыштың бәрінің нысанаға тигізбеуі; г) ең болмаса біреуінің нысанаға тигізбеуі.Жауабы: а)0,336; ә)0,188; б) 0,452; в) 0,024; г) 0,976. 12. 500 механизмнің 240 бірінші сортқа, 160 екінші сортқа; 100 үшінші сортқа жатады. Бірінші сортқа тиісті механизмердің ішінде сапасыз механизм болу ықтималдығы 0,03, екінші сортқа тиістілердің арасында – 0,04, үшінші сортқа тиістілердің арасында – 0,05 тең болсын. Кез келген бір механизм алынған. Оның а) сапалы; ә) сапасыз екендігінің ықтималдықтарын табу керек. Жауабы: а) 0,9628; ә) 0,0372. 13. Дайындалған ыдыстар құймасының 75% бірінші, ал 25% екінші цехта жасалған. Осымен бірге бірінші цехтағы ыдыстардың 5%, ал екіншісіндегі 20% жарамсыз. Кездейсоқ алынған ыдыстың а) ақаусыз; ә) жарамсыз болу ықтималдықтарын табу керек. Жауабы: а) 73/80; ә) 7/80. 14. Қару-жарақ тұратын пирамидада 8 винтовка бар, оның бесеуі оптикалық көздеуішті винтовкалар. Оптикалық көздеуішті винтовкадан атқан оқтың нысанаға тию ықтималдығы 0,96, ал жай винтовка үшін – 0,72 тең. Кездейсоқ алынған винтовкадан бір оқ атылған. Атылған оқтың нысанаға тию ықтималдығын табу керек. Жауабы: 0,87. 15. Болттар дайындайтын фабрикада барлық бұйымдардың 27%-ын бірінші станокта, 35%-ын үшінші станокта шығарады. Бұл станоктарда шығатын болттардың сәйкесінше 6%, 5%, 4%-і жарамсыз болсын. Кездейсоқ алынған болттың а) ақаусыз; ә) жарамсыз болу ықтималдықтарын табу керек. Жауабы: а) 0,9508; ә) 0,0492. 16. Бірінші жәшікте – 10 шар, оның 6-ы қызыл, екіншісінде – 20 шар, оның 4-і қызыл. Екі жәшіктен бір-бір шар алып, содан соң олардың біреуін кездейсоқ аламыз. Осы шардың қызыл шар болу ықтималдығын табу керек. Жауабы: 0,34. 17. Үш атқыш бір-бірден оқ атты, оның екеуі нысанаға тиді. Әрбір атқыштың атқан оқтарының нысанаға тию ықтималдықтары сәйкесінше 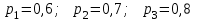 болса, онда тиген екі оқтың біреуі: а) бірінші; болса, онда тиген екі оқтың біреуі: а) бірінші; ә) екінші; б) үшінші атқыштың оғы екендігінің ықтималдықтарын табу керек. Жауабы: а) 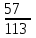 ; ә) ; ә)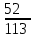 ; б) ; б) 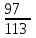 . .18. Бірінші жәшікте 10 шар, оның 6-ы қызыл, екіншісі жәшікте 20 шар, ның 8-і қызыл. Бірінші жәшіктен кездейсоқ бір шар алынып екіншісіне салынады. Одан кейін екіншісінен бір шар алынады. Ол қызыл шар болсын. Осы шардың бірінші жәшіктің (біріншісінен екіншісіне шар салғанға дейін) шары болу ықтималдығын табу керек. Жауабы: 27/43. 19. Болаттар дайындайтын фабрикада барлық бұйымдардың 45%-ін бірінші машина, 55%-ін екінші машина шығарады. Оларда шығарылатын жарамсыз болттар сәйкесінше 5% және 8% құрайды. Кездейсоқ алынған болт жарамсыз. Осы жарамсыз болтты а) бірінші, ә) екінші машина жасағандығының ықтималдықтарын есептеу керек. Жауабы: а) 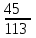 ; ә) ; ә)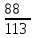 . .20. Өндірістік бөлімшеде 20 жабдық жұмыс істейді. Оның ішінде 9-ы А дәрежелі, 7-уі В дәрежелі, 4-і С дәрежелі. Дайындалған бөлшектердің сапасы өте жақсы болу ықтималдығы сәйкесінше 0,9; 0,8; 0,7. Кездейсоқ таңдап алған бөлшек жарамсыз болып шықты. Оның: а) А дәрежелі; ә) В дәрежелі; б) С дәрежелі жабдықтың дайындаған бөлшегі екендігінің ықтималдығын табу керек. Жауабы: а)9/35; ә)14/35; б) 12/35. 21. Қару-жарақ тұратын пирамидада 15 винтовка бар. Оның 8-і оптикалық көздеуішті винтовка. Оптикалық көздеуішті винтовкадан атқан оқтың нысанаға тию ықтималдығы 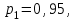 ал жай винтовка үшін – 0,7. Кездейсоқ алынған винтовадан бір оқ атылды және ол нысанаға тиді. Нысанаға тиген оқ: а) оптикалық көздеуішті винтовкадан; ә) жай винтовкадан атылғандығының ықтималдығын табу керек. ал жай винтовка үшін – 0,7. Кездейсоқ алынған винтовадан бір оқ атылды және ол нысанаға тиді. Нысанаға тиген оқ: а) оптикалық көздеуішті винтовкадан; ә) жай винтовкадан атылғандығының ықтималдығын табу керек. Жауабы: а)0,608; ә)0,392. 22. Тиын 8 рет лақтырылды. 5 рет “цифр” жағының түсу ықтималдығын табу керек. Жауабы: 7/32. Бақылау сұрақтары Ең болмаса бір оқиғаның пайда болу ықтималдығы. Толық ықтималдық формуласының мағынасы неде? Бейес формуласының мағынасы неде? |
