17. Канонические уравнения прямой в пространстве. Уравнение прямой в пространстве, проходящей через две данные точки. Общее уравнение прямой в пространстве
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
17. Канонические уравнения прямой в пространстве. Уравнение прямой в пространстве, проходящей через две данные точки. Общее уравнение прямой в пространстве.Канонические уравнения прямой в пространстве.  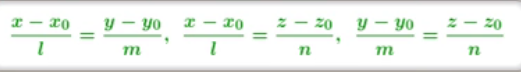 Первые из этих двух уравнений независимые, а третье является следствием. Где каждое уравнение является уравнением плоскости, содержащим данную прямую L. Первые из этих двух уравнений независимые, а третье является следствием. Где каждое уравнение является уравнением плоскости, содержащим данную прямую L.Например, вычитая из первого второе , мы приходим к третьему уравнению. Уравнение прямой в пространстве, проходящей через 2 точки.  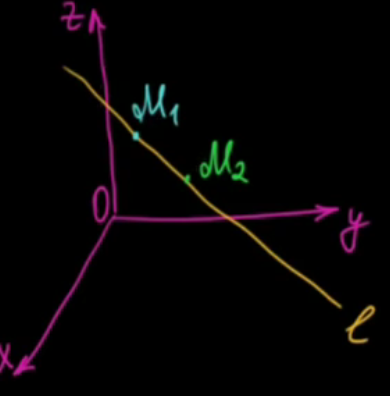 Пусть М 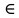 L. При этом М имеет координаты (x,y,z). L. При этом М имеет координаты (x,y,z). Рассмотрим вектор 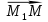 и вектор и вектор 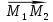 и найдём их координаты. и найдём их координаты.Н 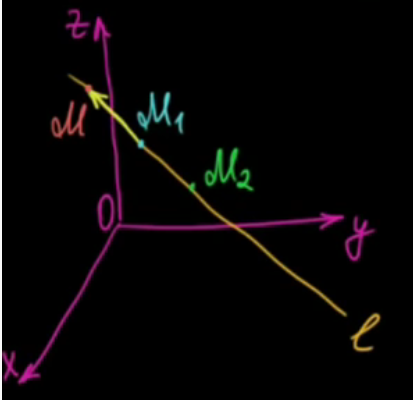 айдём координаты: айдём координаты: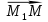 = (X-X1, Y-Y1, Z-Z1) = (X-X1, Y-Y1, Z-Z1)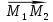 = (X2-X1, Y2-Y1, Z2-Z1) = (X2-X1, Y2-Y1, Z2-Z1)Векторы 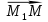 и и 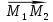 лежат на одной прямой L, следовательно они коллинеарны, значит их соответствующие координату пропорциональны по свойству коллинеарных векторов. лежат на одной прямой L, следовательно они коллинеарны, значит их соответствующие координату пропорциональны по свойству коллинеарных векторов. 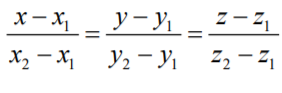 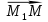 || || 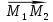 = = Это и есть уравнение прямой, проходящей через 2 заданные точки. Общее уравнение прямой в пространстве Пусть в пространстве задан вектор 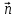 с координатами (А,В,С). Существует огромное количество параллельных плоскостей параллельных друг другу и перпендикулярных с координатами (А,В,С). Существует огромное количество параллельных плоскостей параллельных друг другу и перпендикулярных 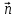 . Выберем одну из них, следовательно вектор . Выберем одну из них, следовательно вектор 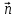 перпендикулярный плоскости P, называется нормалью (вектор нормали). перпендикулярный плоскости P, называется нормалью (вектор нормали). Пусть Mo – фиксированная точка плоскости Р, а M – произвольная точка плоскости Р.  Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и известно, что прямая L является линией пересечения двух плоскостей a1 и а2. К 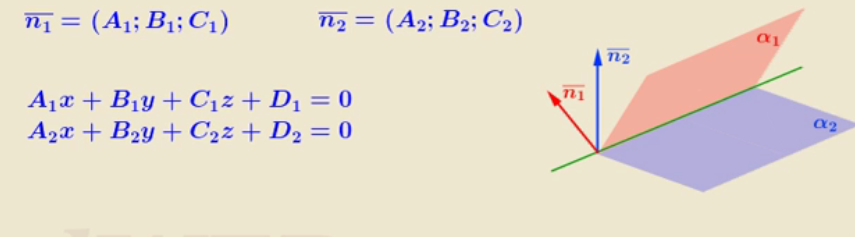 аждая из плоскостей задана общим уравнением. аждая из плоскостей задана общим уравнением. 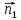 – вектор нормали к плоскости a1. – вектор нормали к плоскости a1.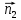 – вектор нормали к плоскости а2. – вектор нормали к плоскости а2.Координаты x,y,z – координаты точек, принадлежащих прямой L. 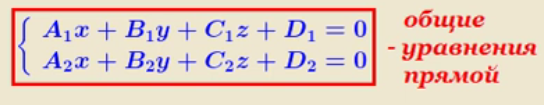 |
