зачеты физ. 17 Основные понятия и определения колебательных процессов. Механические колебания. Гармонические колебания. Незатухающие колебания
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
17) Основные понятия и определения колебательных процессов. Механические колебания. Гармонические колебания. Незатухающие колебания. Колебаниями называются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Колебания присущи всем явлениям природы: колеблется температура воздуха, вода в морях и океанах Колебания разнообразны по своей физической природе: механические колебания тела, подвешенного на пружине (пружинный маятник), качания маятников, колебания струн, вибрации фундаментов зданий, электромагнитные колебания в колебательном контуре и др. Разнообразные по природе, колебания могут иметь общие закономерности и описываться однотипными математическими методами. Колебания бывают периодическими и непериодическими. Если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени, то колебания называются периодическими. Время, за которое совершается одно полное колебание, называется периодом колебания Т. 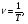 Число полных колебаний, совершающихся за единицу времени, называется частотой периодических колебаний ν: Число полных колебаний, совершающихся за единицу времени, называется частотой периодических колебаний ν:В физике особо выделяются механические и электромагнитные колебания и их комбинации. 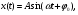 Периодические колебания физической величины х, происходящие по закону синуса или косинуса Периодические колебания физической величины х, происходящие по закону синуса или косинуса (1) 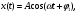 (1а) (1а)называются гармоническими. Здесь А, ω, φ0 - постоянные величины и А>0, ω>0. Величина А, равная наибольшему абсолютному значению колеблющейся физической величины, называется амплитудой колебаний; φ = ωt+φ0 - фаза колебаний, φ0 - начальная фаза (φ= φ0 при t=0). Если колебания системы происходят по закону (1) и на нее не действуют никакие внешние силы, то она может совершать колебания бесконечно долго. Рассеяния энергии при этом не происходит, и колебания называются незатухающими. Амплитуда незатухающих колебаний не зависит от времени. 18) Затухающие колебания. Вынужденные колебания. Резонанс. Автоколебания. 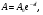 Колебания, энергия которых уменьшается с течением времени, называются затухающими. Убыль энергии связана с действием сил трения в колеблющейся системе и других сил сопротивления. Если для гармонических периодических колебаний амплитуда постоянна, то амплитуда затухающих колебаний изменяется по закону Колебания, энергия которых уменьшается с течением времени, называются затухающими. Убыль энергии связана с действием сил трения в колеблющейся системе и других сил сопротивления. Если для гармонических периодических колебаний амплитуда постоянна, то амплитуда затухающих колебаний изменяется по законуЗначения физических величин, характеризующих затухающие колебания, никогда не повторяются, т.е. затухающие колебания являются непериодическими. Незатухающие колебания системы, вызываемые действием на нее внешней периодической силы F(t), называются вынужденными. Сила F(t) называется возмущающей или вынуждающей силой. 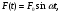 Если F(t) меняется по гармоническому закону Если F(t) меняется по гармоническому закону(6) 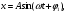 то соответствующие вынужденные колебания могут быть также гармоническими с частотой вынуждающей силы: то соответствующие вынужденные колебания могут быть также гармоническими с частотой вынуждающей силы:(7) где А - амплитуда вынужденных колебаний физической величины, φ1 - разность фаз между вынужденными колебаниями величины х и силы F(t). 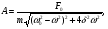 Амплитуда установившихся вынужденных колебаний дается формулой Амплитуда установившихся вынужденных колебаний дается формулой(8) где F0 - амплитуда возмущающей силы, m- масса колеблющейся системы, ω0- циклическая частота свободных незатухающих колебаний системы, ω- циклическая частота внешней силы, δ-коэффициент затухания Явление возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к значению ωрез называется резонансом Величина ωрез называется резонансной циклической частотой, а кривые зависимости А отω (рис. 5) – резонансными кривыми. Форма резонансных кривых зависит от величины коэффициента затухания δ . Резонанс может иметь место в различных сооружениях и машинах, когда в них периодически меняются нагрузки. С явлением резонанса приходится считаться при движении любых машин: вибрации, возникающие при работе двигателя, могут стать опасными, если они будут в резонансе с какими-либо из собственных колебаний конструкции. Система, совершающая незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами, называется автоколебательной системой. Любая автоколебательная система состоит из четырех частей:
19) Механические (упругие) волны. Основные характеристики волн. Уравнение плоской волны. Поток энергии и интенсивность волны. Вектор Умова. Среда называется упругой, если между ее частицами существуют силы взаимодействия, препятствующие какой-либо деформации этой среды. Пусть какое-либо тело совершает колебания в упругой среде. Тогда оно воздействует на частицы среды, прилегающие к нему и заставляет совершать их вынужденные колебания. Среда вблизи колеблющегося тела деформируется и в ней возникают упругие силы, которые действуют на все более удаленные точки среды, выводя их из положения равновесия. Таким образом, с течением времени все частицы среды вовлекаются в колебательное движение. Для распространения колебаний необязательно наличие упругой среды. Например, электромагнитные колебания могут распространяться и в вакууме. Любое возмущение состояния вещества или поля, распространяющиеся в пространстве с течением времени называются волнами. Так, звуковые волны в газах или жидкостях – это колебания давления в этих средах. Механические возмущения, распространяющиеся в упругой среде, называются упругими волнами. Тело, вызывающее возмущение среды, называется источником волн. Геометрическое место точек среды, колеблющихся в одинаковых фазах, называется фронтом волны или волновой поверхностью. Волны бывают продольными и поперечными. Если частицы среды колеблются в направлении, перпендикулярном направлению распространения волны, то волна называется поперечной. Например, волна, распространяющаяся вдоль натянутого резинового шнура с одним закрепленным концом, является поперечной. В продольной волне колебания частиц среды происходят в направлении распространения волны 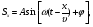 Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох имеет вид Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох имеет вид(12) 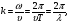 Величина Величина(13) 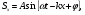 называется волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии, равном 2π единиц длины. С учетом этого, уравнение плоской волны можно переписать в виде называется волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии, равном 2π единиц длины. С учетом этого, уравнение плоской волны можно переписать в видеКолеблющийся источник волн обладает энергией. В процессе распространения волны каждая частица среды, до которой доходит волна, также колеблется и имеет энергию. 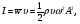 Интенсивностью волны Iназывается величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны: Интенсивностью волны Iназывается величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны:(17) 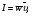 где ʋ- скорость распространения волны. В векторной форме где ʋ- скорость распространения волны. В векторной форме(18) называется вектором Умова. 20) Внутреннее трение(вязкость жидкости). Формула Ньютона. Ньютоновские и неньютоновские жидкости. Ламинарное и турбулентное течения жидкости. Формула Гагена-Пуазейля. В реальной жидкости между молекулами действуют силы взаимного притяжения, обусловливающие внутреннее трение(вязкость). Ньютон установил, что сила внутреннего трения между двумя слоями жидкости, движущимися с различными скоростями, зависит от природы жидкости и прямо пропорциональная площади соприкасающихся слоев и градиенту скорости между ними: Fтр=ȠS dv/dz где Ƞ- коэффициент пропорциональности, называемый коэффициентом вязкости или просто вязкостью жидкости и зависящий от ее природы Сила трения действует касательно к поверхности соприкасающихся слоев жидкости, ускоряет слой, движущийся более медленно и замедляет слой, движущийся более быстро. Градиент скорости характеризует быстроту изменения скорости между слоями жидкости, т.е. в направлении, перпендикулярном направлению течения жидкости У большинства жидкостей (вода, истинные растворы, расплавленные металлы и их соли) коэффициент вязкости зависит от природы жидкости и температуры: с повышением температуры коэф. вязкости уменьшается. Такие жидкости называют ньютоновскими, а их вязкость называется нормальной. У высокомолекулярных жидкостей (растворы полимеров) или представляющих дисперсные системы (суспензии и эмульсии) коэф вязкости зависит также от режима течения – давления и градиента скорости. Такие жидкости называют неньютоновскими , а их вязкость называется аномальной. К неньютоновским жидкостям относится кровь При относительно невысокой скорости течения по трубам небольшого диаметра, движение жидкости имеет ламинарный характер Распределение скоростей по сечению круглой трубы имеет параболический характер V= P1-P2 / 4LȠ (R²-r²) Где Р1 и Р2 – давления в начале и конце участка трубы длиной L, Ƞ - коэффициент вязкости жидкости, R-радиус трубы, r-радиус рассматриваемого слоя жидкости. Максимальная скорость наблюдается в центре трубы: V (max) = P1-P2 / 4LȠ R² Ламинарное течение устанавливается в трубах с гладкими стенками, без резких изменений площади сечения или изгибов трубы, при отсутствии множественных разветвлений. При нарушении этих условий, и особенно при высоких скоростях течение переходит в турбулентное. Для него характерны местные изменения давления в жидкости, сопровождающиеся звуковыми явлениями (шум, журчание) Скорость Vкр перехода ламинарного течения в турбулентное определяется числом Рейнольдса Re: Re=V(кр)РD / Ƞ где Р – плотность жидкости, D – диаметр трубы. Q=(P1-P2)/L × ПR⁴/ 8Ƞ - формула Гагена Пуазейля. Ее можно записать в виде: Q=P1-P2/X Где X= 8LȠ / ПR⁴ называется гидравлическим сопротивлением. 21) Звук. Виды звуков. Физические хар-ки звука. Хар-ки слухового ощущения и их связь с физ хар-ми звука. Шкала уровней интенсивности звука. Звук- распространяющееся в виде продольных волн колебательное движение частиц упругой среды с частотой, воспринимаемых человеческим ухом, т.е. в среднем от 16 до 20000 Гц. Звук с частотой ниже слышимого диапазона называется инфразвуком, выше-ультразвуком. Звуки разделяются на тоны (музыкальные звуки), шумы извуковые удары. Тоном называется звук, являющимся периодическим процессом. Если этот процесс гармонический, то тон называется простым (например, звук камертона). К сложным тонам относятся ангармонические колебания (например, гласные звуки речи человека, звуки музыкальных инструментов). Сложный тон может быть разложен на простые Набор частот с указанием их амплитуды называется акустическим спектром. Спектр сложного тона – линейчатый Шумом называется звук, отличающийся сложной неповторяющейся временной зависимостью (согласные звуки речи, аплодисменты, звуки от вибрации машин и т.д.). Шум можно рассматривать как сочетание беспорядочно изменяющихся сложных тонов. Спектр шума сплошной Звуковой удар – это кратковременное звуковое воздействие (например, взрыв, хлопок).  Энергетической характеристикой звука как механической волны является интенсивность. Но на практике для оценки звука удобнее использовать звуковое давление, которое дополнительно возникает при прохождении звуковых волн в жидкостях или газах. Интенсивность I и звуковое давление pсвязаны соотношением Энергетической характеристикой звука как механической волны является интенсивность. Но на практике для оценки звука удобнее использовать звуковое давление, которое дополнительно возникает при прохождении звуковых волн в жидкостях или газах. Интенсивность I и звуковое давление pсвязаны соотношением(1) где ρ-плотность среды, с – скорость звука. В слуховом ощущении субъективно различаются высота, громкость и тембрзвука. Каждая из этих характеристик, в свою очередь, зависит от физических величин, имеющих объективный смысл: частоты и интенсивности звуковой волны. Высота тона зависит от частоты колебаний. Чем больше частота, тем выше кажется звук. Музыкальные звуки с одним и тем же основным тоном различаются тембром, который, в основном, определяется частотами и амплитудами обертонов. Мы узнаем знакомые голоса и музыкальные инструменты именно по тембру. Громкость звука зависит от интенсивности звука. Наименьшая интенсивность звуковой волны, которая может быть воспринята органами слуха называется порогом слышимости I0. Стандартный порог слышимости принимается равным I0 =10-12 Вт/м2 при основной частоте 1 кГц. Наибольшая интенсивность звуковой волны, при которой восприятие звука не вызывает болевого ощущения, называется порогом болевого ощущения или порогом осязания. Порог осязания зависит от частоты звука и изменяется от 0,1 Вт/м2 при 6 кГц до 10 Вт/м2 при низких и звуковых частотах. Диапазон интенсивностей воспринимаемых нами звуков очень велик. 22) Закон Вебера-Фехнера. Шкала уровней громкости звука. Кривые равной громкости. В основе создания шкалы уровней громкости лежит психофизический закон Вебера-Фехнера: если раздражение увеличивается в геометрической прогрессии (т.е. в одинаковое число раз), то ощущение этого раздражения возрастает в арифметической прогрессии (т.е. на одинаковую величину). Применительно к звуку это означает, что если интенсивность звука принимает ряд последовательных значений, например aI0, a2I0, а3I0, … (а – некоторый коэффициент, а>1), то соответствующие им ощущения громкости звука Е0, 2Е0, 3Е0, … Математически это означает, что громкость звука пропорциональна логарифму интенсивности звука. Если действуют два звуковых раздражения с интенсивностями Iи I0, причем I0 – порог слышимости, то на основании закона Вебера-Фехнера громкость относительноI0 связана с интенсивностью следующим образом: 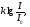 Е= (4) где k-коэффициент пропорциональности 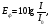 Условно считают, что на частоте 1 кГц шкалы громкости и интенсивности звука полностью совпадают Условно считают, что на частоте 1 кГц шкалы громкости и интенсивности звука полностью совпадают(5) Для отличия от шкалы интенсивности звука в шкале громкости децибелы называют фонами (фон). Громкость на других частотах можно измерить, сравнивая исследуемый звук со звуком частотой 1 кГц. На практике громкость звука можно оценить по так называемым кривым равной громкости, Каждая из кривых объединяет звуки одной и той же громкости, измеряемой в фонах. При этом принято, что громкость любого звука в фонах совпадает с уровнем интенсивности равногромкого звука (в децибелах) на частоте 1 кГц: кривой порога слышимости соответствует уровень громкости 0 фон. 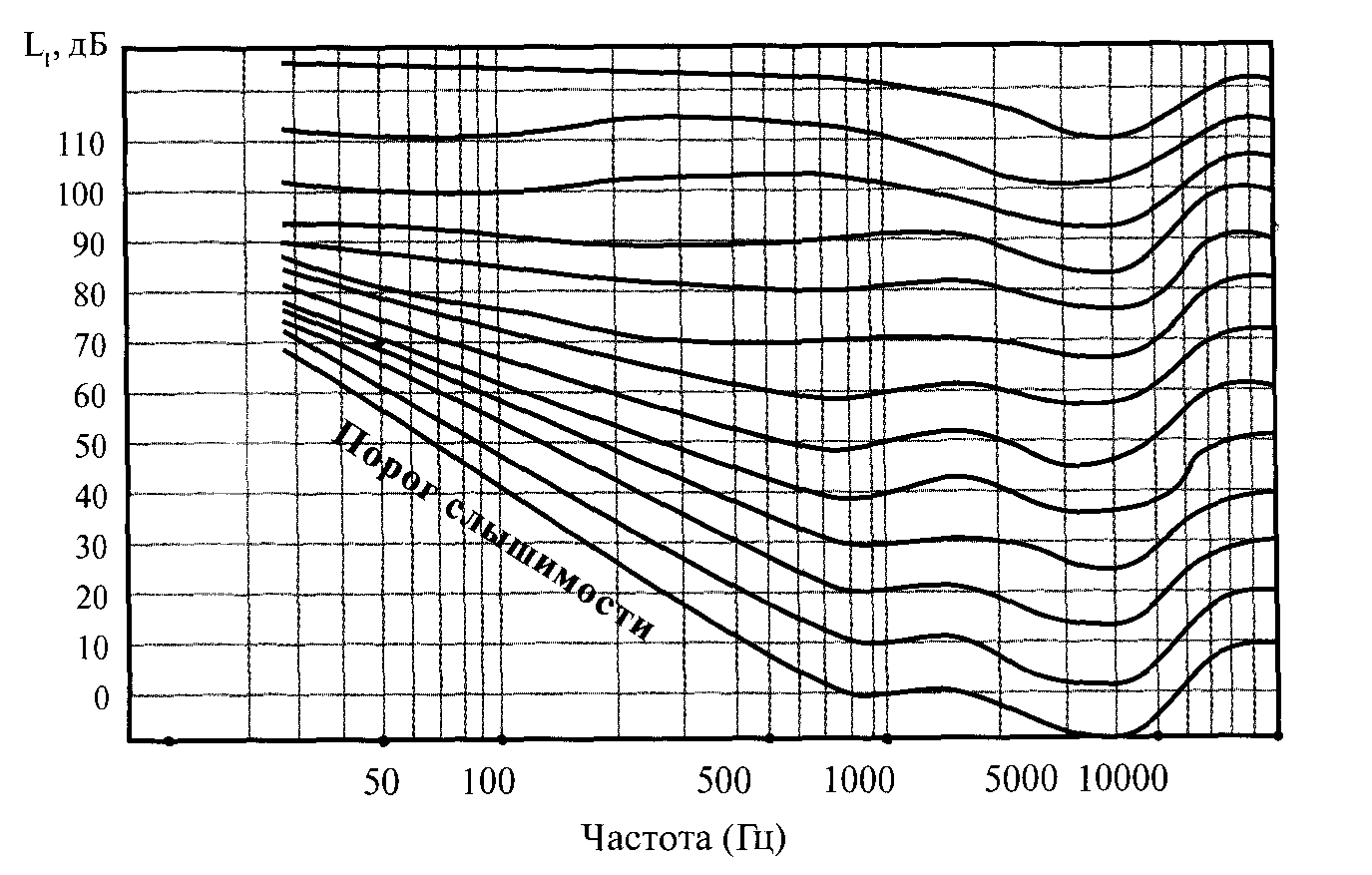 Каждая промежуточная кривая отвечает одинаковой громкости, но разной интенсивности звука для разных частот. По отдельной кривой равной громкости можно найти интенсивности, которые при определенных частотах вызывают ощущение этой громкости. Используя совокупность кривых равной громкости, можно найти для разных частот громкости, соответствующие определенной интенсивности. Метод измерения остроты слуха называется аудиометрией:на специальном приборе (аудиометре) определяют порог слухового ощущения на разных частотах; полученная кривая называется аудиограммой. Сравнивая аудиограмму пациента с нормальной кривой порога слухового ощущения, можно диагностировать заболевание органов слуха. |
