Экзамены мат.. 18) Функция многих переменных. Скалярные и векторные поля. Примеры. окрестность точки r0 Rn. Внутренние, внешние и граничные точки множества.
 Скачать 136.26 Kb. Скачать 136.26 Kb.
|
23. Вывод формулы для производной сложной функции. Пусть функция z=f(x,y) – функция двух переменных, x и y, каждая из которых является функцией независимой переменной t, 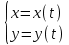 В этом случае функция z=f(x(t),y(t)) является сложной функцией одной независимой переменной t; переменные x и y – промежуточные переменные. В этом случае функция z=f(x(t),y(t)) является сложной функцией одной независимой переменной t; переменные x и y – промежуточные переменные.Теорема: Если z=f(x,y) – дифференцируемая в точке 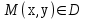 функция и функция и 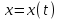 и и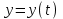 — дифференцируемые функции независимой переменной t, то производная сложной функции z=f(x(t),y(t)) вычисляется по формуле: — дифференцируемые функции независимой переменной t, то производная сложной функции z=f(x(t),y(t)) вычисляется по формуле: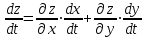 Доказательство: Дадим независимой переменной tприращение Доказательство: Дадим независимой переменной tприращение 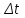 . Тогда функции . Тогда функции 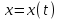 и и 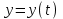 получат приращения получат приращения 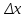 и и 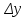 соответственно. В результате получим приращение функции соответственно. В результате получим приращение функции 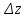 . Поскольку функция дифференцируема в точке . Поскольку функция дифференцируема в точке 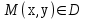 , то ее полное приращение можно записать в виде: , то ее полное приращение можно записать в виде: 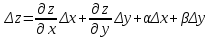 , где , где 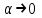 , , 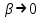 при при 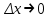 , , 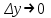 . Разделим выражение . Разделим выражение 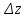 на на 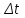 и перейдем к пределу при и перейдем к пределу при 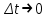 . Тогда . Тогда 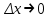 и и 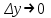 , в силу непрерывности функций , в силу непрерывности функций 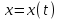 и и 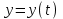 (по условию теоремы они – дифференцируемы, а следовательно - непрерывны). (по условию теоремы они – дифференцируемы, а следовательно - непрерывны). 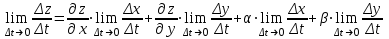 , ,то есть 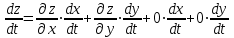 , или , или 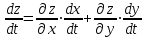 . .Частный случай: z=f(x,y), где y=y(x), то есть z=f(x,y(x)) – сложная функция одной независимой переменной x. Этот случай сводится к предыдущему, причем роль независимой переменной t выполняет x: 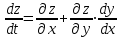 - формула полной производной. - формула полной производной.Общий случай: z=f(x,y), где x=x(u,v), y=y(u,v) то есть z=f(x(u,v),y(u,v)) – сложная функция независимых переменных u и v, частные производные которой находятся по формулам: 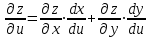 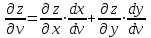 Таким образом, производная сложной функции z по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции по ее промежуточным переменным на их производные по соответствующей независимой переменной. 24. Производная функции, заданной неявно. Определение:Функция 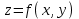 называетсянеявной, если она задается уравнением называетсянеявной, если она задается уравнением 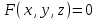 неразрешимым относительно z. неразрешимым относительно z.Начнем рассмотрение с неявной функции одного переменного :F(x,y)=0. Теорема:Пусть непрерывная функция y(x) задается неявно уравнением вида F(x,y)=0 и 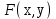 , , 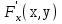 , , 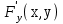 - непрерывные функции в области D, содержащей точку (x,y), удовлетворяющую уравнению F(x,y)=0. Кроме того, в этой точке - непрерывные функции в области D, содержащей точку (x,y), удовлетворяющую уравнению F(x,y)=0. Кроме того, в этой точке 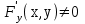 , тогда функция y(x) имеет производную , тогда функция y(x) имеет производную 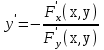 . .Доказательство:Пусть некоторому значению x соответствует значение y, причем выполняется F(x,y)=0. Возьмем для независимой переменной x приращение 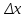 . Функция y, при этом, получит приращение . Функция y, при этом, получит приращение 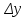 . То есть значению аргумента . То есть значению аргумента 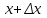 будет соответствовать значение функции будет соответствовать значение функции 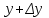 . А в силу уравнения F(x,y)=0 имеем: . А в силу уравнения F(x,y)=0 имеем: 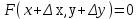 и, соответственно и, соответственно 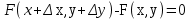 . Левую, часть, являющуюся полным приращением функции двух переменных можно представить в виде . Левую, часть, являющуюся полным приращением функции двух переменных можно представить в виде 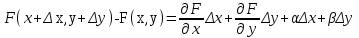 , где , где 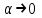 , , 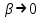 , при , при 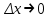 и и 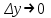 . Или иначе (поскольку правая часть равенства - ноль): . Или иначе (поскольку правая часть равенства - ноль): 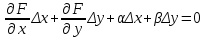 Разделим последнее равенство на Разделим последнее равенство на 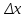 и вычислим и вычислим 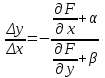 .Устремим .Устремим 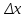 к нулю. Тогда учитывая, что к нулю. Тогда учитывая, что 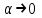 , ,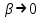 , при , при 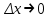 и и 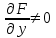 в пределе получим в пределе получим 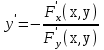 . Таким образом, доказана теорема существования производной от функции, заданной неявно. . Таким образом, доказана теорема существования производной от функции, заданной неявно.Рассмотрим теперь функцию вида 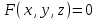 . Найдем частные производные функции неявной функции z. Для этого подставив в уравнение вместо z, . Найдем частные производные функции неявной функции z. Для этого подставив в уравнение вместо z, 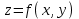 , получим тождество , получим тождество 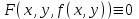 . Частные производные функциитождественно равной нулю также равны нулю. . Частные производные функциитождественно равной нулю также равны нулю.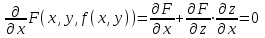 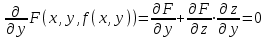 Откуда: 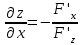 , ,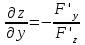 . .Аналогично определяются производные неявно заданных функций произвольного числа переменных. 25) Гиперповерхность и поверхность уровня. Касательная плоскость и нормаль к поверхности Рассмотрим точки области в которых функция принимает одинаковое значение 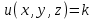 . Множество таких точек образуют некоторую поверхность, называемую поверхностью уровня. . Множество таких точек образуют некоторую поверхность, называемую поверхностью уровня.Гиперповерхность является обобщением понятия поверхности 3-мерного пространства для n-мерного пространства; это многообразие размерности n, которое вложено в евклидово пространство на единицу большей размерности n + 1. Касательная плоскость к поверхности в её точке М0 (точка касания) есть плоскость, проходящая через М0 и содержащая в себе все касательные, проведённые в точке М0 ко всевозможным кривым, проведённым на поверхности через точку М0 Нормалью к поверхности в точке М0 называется прямая, проходящая через точку М0 и перпендикулярная к касательной плоскости, проведённой в этой точке. Если уравнение поверхности имеет вид F(x, y, z)=0, то уравнение касательной плоскости в точке Уравнение нормали к этой поверхности в точке М0 есть В случае явного задания поверхности уравнением (8.1) и (8.2) примут вид 30. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла Свойства неопределенного интеграла.
31. Занесение под знак дифференциала и замена переменной в неопределенном интеграле. Замена переменных в неопределенном интеграле. Пусть ф. является диф-мой и обратимой Пример: = 32. Интегрирование по частям в неопределенном интеграле. Интегралы вида Интегр. по частям применяют, когда сложный интеграл можно заменить интегрир. более простого. 1. Подынтегр. ф. представляет собой произв. многочле-на на показ. ф. или тригонометр.. За u берется многочлен, за dv – оставшуюся часть подынтегрального выражения. 2. Подынтгр. ф. представляет собой произв. многочлена на логариф. или обратную тригонометр. Ф.. За часть u нужно взять логарифм. или обратную тригонометр. ф.. 3. Подынтегр. ф. представляет собой произведение три-гонометр. на показательную ф.. Не важно что брать за u. 4. Иногда метод интегрирования по частям приходится применять несколько раз. | ||||||||||||||||||||||||

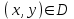 единственное значение
единственное значение 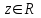 называется функцией двух переменных
называется функцией двух переменных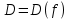 называетсяобластью определения функции; множество значений, принимаемых z в области определения называется областью значений функции, обозначается E или E(f).
называетсяобластью определения функции; множество значений, принимаемых z в области определения называется областью значений функции, обозначается E или E(f).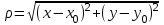 . Рассмотрим неравенство < или
. Рассмотрим неравенство < или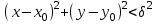 . Это неравенство задает внутреннюю область круга с центром в точке M0 и радиусом , которую называют
. Это неравенство задает внутреннюю область круга с центром в точке M0 и радиусом , которую называют 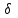 -окрестностью точки.
-окрестностью точки.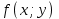 при xx0, yy0 в точке
при xx0, yy0 в точке 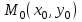 , если для любого, сколь угодно малого положительного , найдется , зависящее от , положительное, такое, что из неравенства
, если для любого, сколь угодно малого положительного , найдется , зависящее от , положительное, такое, что из неравенства 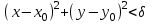 , будет следовать неравенство
, будет следовать неравенство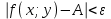 , при условии что
, при условии что 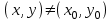 .
. 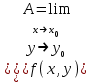
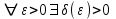 из неравенства
из неравенства 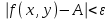 .
. 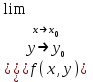 =
=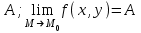
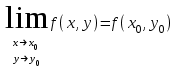 ,то есть если предел в точке
,то есть если предел в точке