Главная страница
Навигация по странице:

  • В каждой стопке три карточки: треугольная, круглая и квадратная. В скольких стопках треугольная карточка лежит выше квадратной

  • 1.2 Карточку, изображённую справа, перевернули сначала через левый край, а потом – через нижний край. Что получилось

  • (А) (Б) (В) (Г) (Д) 1.3 Сейчас отражение часов в зеркале выглядит так, как показано на картинке справа. А как оно выглядело 10 минут назад

    		•

    олимпиада по математике. олимпиада. 18. Когда Робинзон Крузо попал на необитаемый остров, у него было 200 ружейных зарядов. Ради их экономии он решил каждый день тратить на охоте не более 5% имеющихся на то утро зарядов


    Скачать 121.3 Kb.
    Название18. Когда Робинзон Крузо попал на необитаемый остров, у него было 200 ружейных зарядов. Ради их экономии он решил каждый день тратить на охоте не более 5% имеющихся на то утро зарядов
    Анкоролимпиада по математике
    Дата21.11.2022
    Размер121.3 Kb.
    Формат файлаdocx
    Имя файлаолимпиада.docx
    ТипДокументы
    #802877

    6 класс

    18. Когда Робинзон Крузо попал на необитаемый остров, у него было 200 ружейных зарядов. Ради их экономии он решил каждый день тратить на охоте не более 5% имеющихся на то утро зарядов. В какой-то момент Робинзон уже не мог делать выстрелы, придерживаясь своего правила. Сколько патронов он истратил к этому моменту?

    Ответ: 181. Если Робинзон не смог сделать выстрел по правилам, то один заряд – это больше, чем 5% имевшихся зарядов. Тогда 20 зарядов – это больше, чем 100% имевшихся зарядов, то есть у него их осталось не более 19. С другой стороны, вчера патронов было хотя бы 20, а осталось не меньше 95% от этого количества, то есть их осталось хотя бы 19. Поэтому Робинзон потратил 200–19=181 патрон.

    (6– 7). Вставьте вместо каждой звёздочки цифру так, чтобы произведение трёх десятичных дробей равнялось натуральному числу. Использовать ноль нельзя, зато остальные цифры могут повторяться. *,* · *,* · *,* = *

    1. Ответ: например, 1,5 · 1,6 · 2,5 = 6 или 1,5 · 2,4 · 2,5 = 9. Чтобы найти ответ, домножим каждое число в левой части на 10, а правую часть, соответственно, на 1000: ** · ** · ** = *000. Правая часть делится на 1000 = 2³ · 5³, а ни одно из чисел в левой части одновременно на 2 и 5 не делится (иначе оно оканчивается на 0). Значит, одно из левых чисел делится на 5²=25, какое-то другое – на 2³=8 (то есть оно как минимум 16), а третье – на 5 (чтобы произведение делилось на 5³) и оно нечётно (то есть это как минимум 15). Вариант 25·16·15=6000 подходит.

    31. В этом году в феврале встретилась дата-палиндром: 22.02.2022 (цифры слева направо идут в том же порядке, что и  справа налево). Найдите следующую ближайшую дату-палиндром (и докажите, что она действительно ближайшая)

    31. В этом году в феврале встретилась дата-палиндром: 22.02.2022 (цифры слева направо идут в том же порядке, что и справа налево). Найдите следующую ближайшую дату-палиндром (и докажите, что она действительно ближайшая)

    . Ответ: 03.02.2030. В этом году другой даты-палиндрома уже не будет (ведь 4 цифры года определяют всю дату), и в годы с 2023 по 2029 тоже: при чтении в обратном порядке они дадут числа, которые больше количества дней в месяцах (32, 42, …, 92). А в 2030 году будет 03.02.2030.

    11. Барон Мюнхгаузен утверждает, что записал дробь A/B, где A и B – различные натуральные числа, а потом вычеркнул какую-то цифру в числителе и какую-то – в знаменателе так, что получившаяся дробь стала равна дроби B/A. Могло ли такое быть? Ответ: Да, могло. Например, 14/28 f 4/2.

    Каждый из 10 школьников должен был купить в поход по 2 кг крупы. Но крупа продавалась в пачках, весивших меньше килограмма, и часть школьников взяли по три пачки (с запасом), а часть – по две (с  недостачей). В итоге всё равно получилось ровно 20  кг крупы. Сколько весила одна пачка, если её масса в граммах целая?

    Ответ: 800 г. Всего крупы у нас 20 000 г. Так как каждый из 10 человек взял две пачки (меньше 2 кг) или три пачки (больше 2 кг), а получилось так, будто все взяли по 2 кг, минимум была взята 21 пачка, а максимум – 29. Масса крупы должна делиться на число пачек, но 20 000 получается перемножением двоек и пятёрок, значит, число пачек тоже должно так получаться. Среди чисел от 21 до 29 такое число только одно – 25. Поделив 20 000 на 25, получаем ответ.

    Тане и Ване дали одинаковые многоугольники из бумаги. Таня отрезала от своего листа кусок, и остался квадрат. Ваня отрезал точно такой же (и по форме, и по размеру) кусок по-другому, и у него остался треугольник. Нарисуйте пример, как это могло быть. Т.B. Казицына

    2 (6). Дана бумажная клетчатая фигура с дыркой (см. рисунок). Покажите, как разрезать эту фигуру на две части таким образом, чтобы из этих частей можно было сложить квадрат. Части можно поворачивать и переворачивать, но нельзя накладывать друг на друга. М.А.Евдокимов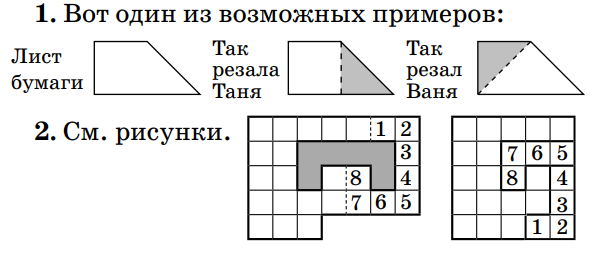





    Задача 6 (7 баллов). За круглым столом сидели 13  гостей. Среди них были рыцари (всегда говорят правду), лжецы (всегда лгут) и марсиане. Про марсиан известно, что правду они говорят только марсианам, а всем остальным лгут. Каждые двое сидящих рядом сказали друг другу: «Ты не рыцарь». Сколько лжецов могло сидеть за столом, если известно, что их было больше, чем марсиан? Найдите все возможные варианты ответа и докажите, что других нет.

    6. Ответ: 4 или 5. Ясно, что рядом со лжецом может сидеть только рыцарь, рядом с рыцарем – только лжец или марсианин, а рядом с марсианином – только рыцарь или марсианин. Если лжецов 3 или меньше, то марсиан 2 или меньше, вместе лжецов и марсиан 5 или меньше, а значит, рыцарей 8 или больше, что невозможно – два рыцаря рядом сидеть не могут. Вот примеры, где лжецов 4 и 5: ММММРЛРЛРЛРЛР и ММРЛРЛРЛРЛРЛР. Заметим, что рыцарей как минимум на 1 больше, чем лжецов, потому что справа от лжеца всегда сидит рыцарь, и ещё справа от хотя бы одного марсианина сидит рыцарь. Если лжецов 6 или больше, то рыцарей хотя бы 7. Тогда двое рыцарей сидят рядом, что невозможно. 7. Ответ: а) нет; б) 2; в) 50

    Задача 1 (2+2 балла). На столе «касса цифр» (набор бумажных карточек с цифрами). Маша выложила из карточек четырёхзначное число. Толя заменил в числе все карточки на другие: каждую цифру либо уменьшил на 4, либо увеличил на 1. Число уменьшилось в 4 раза. Какое число могла выложить Маша? Что могло получиться у Толи? (Найдите как можно больше вариантов ответов). Задача 2 (4 балла)

    На доске написаны в ряд четыре четвёрки: 4 4 4 4. Между каждыми двумя соседними четвёрками надо поставить один из знаков «+», «–», «×» или «:», затем расставить скобки (если потребуется) и вычислить значение. Получите таким способом каждую из цифр от 0 до 9.

    4+4–4–4=0

    4–4+4:4=1

    4:4+4:4=2

    (4+4+4):4=3

    4+(4–4)×4=4

    (4×4+4):4=5

    4+(4+4):4=6

    4+4–4:4=7

    4+4+4–4=8

    4+4+4:4=9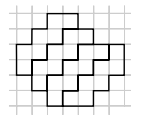

    .

    1.1 На рисунке изображено пять стопок картонных карточек.




    В каждой стопке три карточки: треугольная, круглая и квадратная. В скольких стопках треугольная карточка лежит выше квадратной?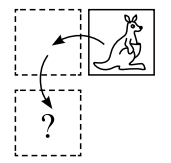

    ( А) 1; (Б) 2; (В) 3; (Г) 4; (Д) 5.


    1.2 Карточку, изображённую справа, перевернули сначала через левый край, а потом – через нижний край. Что получилось?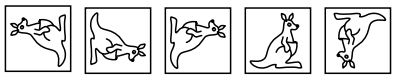



    (А) (Б) (В) (Г) (Д)


    1.3 Сейчас отражение часов в зеркале выглядит так, как показано на картинке справа. А как оно выглядело 10 минут назад?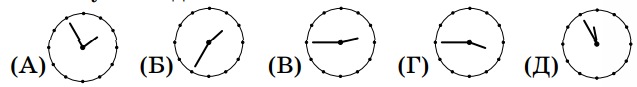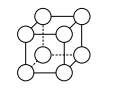



    2. Расставьте цифры от 1 до 8 по одной в вершинах куба таким образом, чтобы для всех шести граней суммы четырёх чисел, стоящих в вершинах одной грани, были различны.

    3 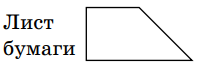. Тане и Ване дали одинаковые многоугольники из бумаги. Таня отрезала от своего листа кусок, и остался квадрат. Ваня отрезал точно такой же (и по форме, и по размеру) кусок по-другому, и у него остался треугольник. Нарисуйте пример, как это могло быть.

    4. На доске написаны в ряд четыре четвёрки: 4 4 4 4. Между каждыми двумя соседними четвёрками надо поставить один из знаков «+», «–», «×» или «:», затем расставить скобки (если потребуется) и вычислить значение. Получите таким способом каждую из цифр от 0 до 9.

    5. Каждый из 10 школьников должен был купить в поход по 2 кг крупы. Но крупа продавалась в пачках, весивших меньше килограмма, и часть школьников взяли по три пачки (с запасом), а часть – по две (с  недостачей). В итоге всё равно получилось ровно 20  кг крупы. Сколько весила одна пачка, если её масса в граммах целая?

    6. В этом году в феврале встретилась дата-палиндром: 22.02.2022 (цифры слева направо идут в том же порядке, что и справа налево). Найдите следующую ближайшую дату-палиндром (и докажите, что она действительно ближайшая)

    1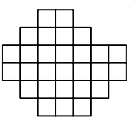. Р азрежьте бумажную клетчатую фигуру на рисунке по линиям сетки на несколько одинаковых, каждая из которых состоит более чем из одной клетки.



    1. На доске написаны в ряд четыре четвёрки: 4 4 4 4. Между каждыми двумя соседними четвёрками надо поставить один из знаков «+», «–», «×» или «:», затем расставить скобки (если потребуется) и вычислить значение. Получите таким способом каждую из цифр от 0 до 9.

    2. Вставьте вместо каждой звёздочки цифру так, чтобы произведение трёх десятичных дробей равнялось натуральному числу. Использовать ноль нельзя, зато остальные цифры могут повторяться. *,* · *,* · *,* = *

    3. Когда Робинзон Крузо попал на необитаемый остров, у него было 200 ружейных зарядов. Ради их экономии он решил каждый день тратить на охоте не более 5% имеющихся на то утро зарядов. В какой-то момент Робинзон уже не мог делать выстрелы, придерживаясь своего правила. Сколько патронов он истратил к этому моменту?

    4. В этом году в феврале встретилась дата-палиндром: 22.02.2022 (цифры слева направо идут в том же порядке, что и справа налево). Найдите следующую ближайшую дату-палиндром (и докажите, что она действительно ближайшая)

    написать администратору сайта