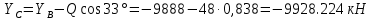1министерство науки и высшего образования российской федерации
 Скачать 1.1 Mb.
|
 1МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Тольяттинский государственный университет
Практическое задание №_1__ по учебному курсу « Механика №1 » (наименование учебного курса) Вариант ____ (при наличии)
Тольятти 2023 Практическое задание 1.Тема 1.2. Произвольная плоская система сил Задание  Жесткая рама (рис. 1.1) закреплена в точке А шарнирно, а в точке D прикреплена к невесомому стержню под углом α, равным 45 + 5П (град). На раму действует пара сил с моментом M, равным C + 1 (кН·м); внешняя сила F равная П + Г (кН), приложенная в точке А (если П = 0… 1), в другой точке В (если П = 2... 3), в точке С (если П = 4... 5), в точке Е (если П = 6... 7), в точке D (если П = 8… 9) под углом β к горизонту, равным 5 + 5Г (град) к горизонтали; распределенная нагрузка с интенсивностью Г (кН/м) вдоль колена АВ (длина которого 1 м) слева (если П = 0), вдоль колена ВС (длина которого 2 м) снизу (если П = 1... 2), вдоль колена АВ справа (если П = 3… 4), вдоль колена ВС сверху (если П = 5), вдоль колена СЕ (длина которого равна Г + 1 (м)) справа (если П = 6), вдоль колена ЕD (длина которого равна С + 1 (м)) сверху (если П = 7), вдоль колена СЕ слева (если П = 8), вдоль колена ЕD снизу (если П = 9). Определите реакции в точках А и D.Бланк выполнения задания 1
Жесткая рама (рис. 1.1) закреплена в точке А шарнирно, а в точке D прикреплена к невесомому стержню под углом α= 45 + 5*8=85 (град). На раму действует пара сил с моментом M=С+1= 2+1=3 (кН·м); сила F= 8 + 5=13 (кН), приложенная в точке А (если П = 0… 1), в другой точке В (если П = 2... 3), в точке С (если П = 4... 5), в точке Е (если П = 6... 7), в точке D (если П = 8… 9) под углом β= 5 + 5*5=30 (град) к горизонтали; распределенная нагрузка с интенсивностью Г (кН/м) вдоль колена АВ (длина которого 1 м) слева (если П = 0), вдоль колена ВС (длина которого 2 м) снизу (если П = 1... 2), вдоль колена АВ справа (если П = 3… 4), вдоль колена ВС сверху (если П = 5), вдоль колена СЕ 5+ 1=6 (м)) справа (если П = 6), вдоль колена ЕD =2 + 1=3 (м)) сверху (если П = 7), вдоль колена СЕ слева (если П = 8), вдоль колена ЕD снизу (если П = 9). Определите реакции в точках А и D.      А          D β    Е М      α   С В     q Рис. 1.1 АВ / =1 (м) /ВС/ = 2 (м) /СЕ/ = 6 (м) /ЕD/ = 3 (м) α = 45 + 5*8 =85(град). M = 2 + 1 = 3(кН*м); F = 8 + 5=13 (кН), в точке Е (если П = 7...9) под углом β = 5 + 5*5=30 (град); q = Г =5 (кН/м) вдоль колена /ЕD/ = 2 + 1=3 (м) сверху (если П = 8...9). Определить реакции в точках А и D. Рассмотрим равновесие РАМЫ К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции. Активные (заданные) силы: F, Q, пара сил с моментом М, где Q- сосредоточенная сила, заменяющая действие распределенной вдоль отрезка ED нагрузки интенсивностью q. Величина Q=q*ED=5*3кН/м*M=15 кН Линия действия силы  проходит через середину отрезка ED.Силы реакции (неизвестные силы):  ее составляющие   - заменяет действие отброшенного подвижного шарнира (опора А).Реакция перпендикулярна поверхности, на которую опираются катки подвижного шарнира.  - составляющие реакции  , заменяют действие отброшенного неподвижного шарнира (опораD).Для полученной плоской произвольной системы сил можно составить три уравнения равновесия:  ,  ,  .Задача является статически определимой Поместим систему координат XY в точку А, ось ОX направим параплельно балке BC. За центр моментов всех сил выберем точку В. Составим уравнения равновесия: 1) ;  kx=0→Xa*cosβ=02)   при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину ED.   момент распределенной нагрузки равен произведению интенсивности q нагрузки на ее длину a и на расстояние от ее середины до рассматриваемой точки a/2+z MС=Rql=qa(a/2+z)  d  Rd- 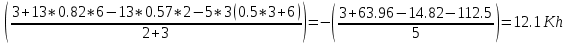 Ya-q*ED-F*cinB+Rd=0 Ya= q*ED-F*cinB-Rd=5*3-13*0.5-12.1=15-6.5-12.1=-5.6kH Проверка В целях проверки взяли уравнение Σ Mb(Fk)=0→ M+F*cosB*EC-F*cinB*BC-q*ED(0.5*ED+BC)+Rd(BC+ED)=0 3+13*0.82*6-13*0.52*2-5*3(0.5*3+5)+12.1(2+3)=0 3+63.96-13.52-112.3+60.5=0 в результате подстановки в правую часть этого равенства данных задачи и найденных сил реакций получили нуль, задача решена - верно. Реакции найдены верно. найдем величину силы реакции неподвижного шарнира Ra=  Практическое задание 2Тема 1.2. Произвольная плоская система сил Задани
2. Рисунок, на котором показаны все реакции на левой балке   3. Рисунок, на котором показаны все реакции на правой балке 
8. Записывается ответ: ХА = -9894,704кН; YА = -7387.884кН; ХВ = 9888 кН; YВ = -9894,704кН; ХС -9928.224кН; YС = -9928.224 кН. |
(1)
(2)
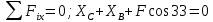(1)
