|
|
1Понятие о волнах плоские волны
 
1Понятие о волнах плоские волны.
Волны- пространственно временной процесс, описывающий распространения колебаний(перенос энергии без переноса вещества).
По своему характеру волны подразделяются на:
По признаку распространения в пространстве: стоячие, бегущие.
По характеру волны: колебательные, уединённые (солитоны).
По типу волн: поперечные, продольные, смешанного типа.
По законам, описывающим волновой процесс: линейные, нелинейные.
По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
По геометрии: сферические (пространственные), одномерные (плоские), спиральные.
Продольные волны: направление колебания среды совпадает с направления распространения волны (скалярные волны).
Поперечные волны: возмущение которых перпендикулярно распространению( акустические, векторные волны).
Плоская волна- та волна у которой временной процесс во всех точках распространения одинаковый.
Плоской называется волна, у которой поверхности равных фаз – параллельные плоскости. Если поверхности равных амплитуд совпадают с поверхностями равных фаз, то такая волна называется однородной. В однородной волне вектора и изменяются в пространстве только вдоль одного направления, перпендикулярно фазовому фронту этой волны и совпадающего с направлением ее распространения.
1.2 Плоская волна, в которой поверхности равных амплитуд не плоскости или плоскости, не совпадающие с поверхностями равных фаз, называется неоднородной.
Источников, возбуждающих плоских волны, в природе не существует, соответственно не существует и плоских волн. Все реальные излучатели на расстояниях, значительно превышающих их линейные размеры, создают сферические волны. Однако, при определенных допущениях, ограниченный участок сферы можно считать плоским. Следовательно, ЭМВ, возбуждаемую реальным излучателем в ограниченной области пространства, находящейся на достаточном удалении от этого излучателя, можно считать плоской. Кроме того, любую волну можно представить в виде суммы элементарных плоских волн, что в ряде случаев существенно упрощает анализ.

S=F(kz-wt)-формула для плоской волны, где к=2П/λ=β ,φ0=βz , z-направление распространение волныэ
V=w/k
|
2Затухание волн в материальных средах
В любой реальной среде амплитуда волнового процесса неизбежно уменьшается по мере распространения,
например за счет тепловых потерь. Закон ослабления амплитуды легко найти из следующих соображений.
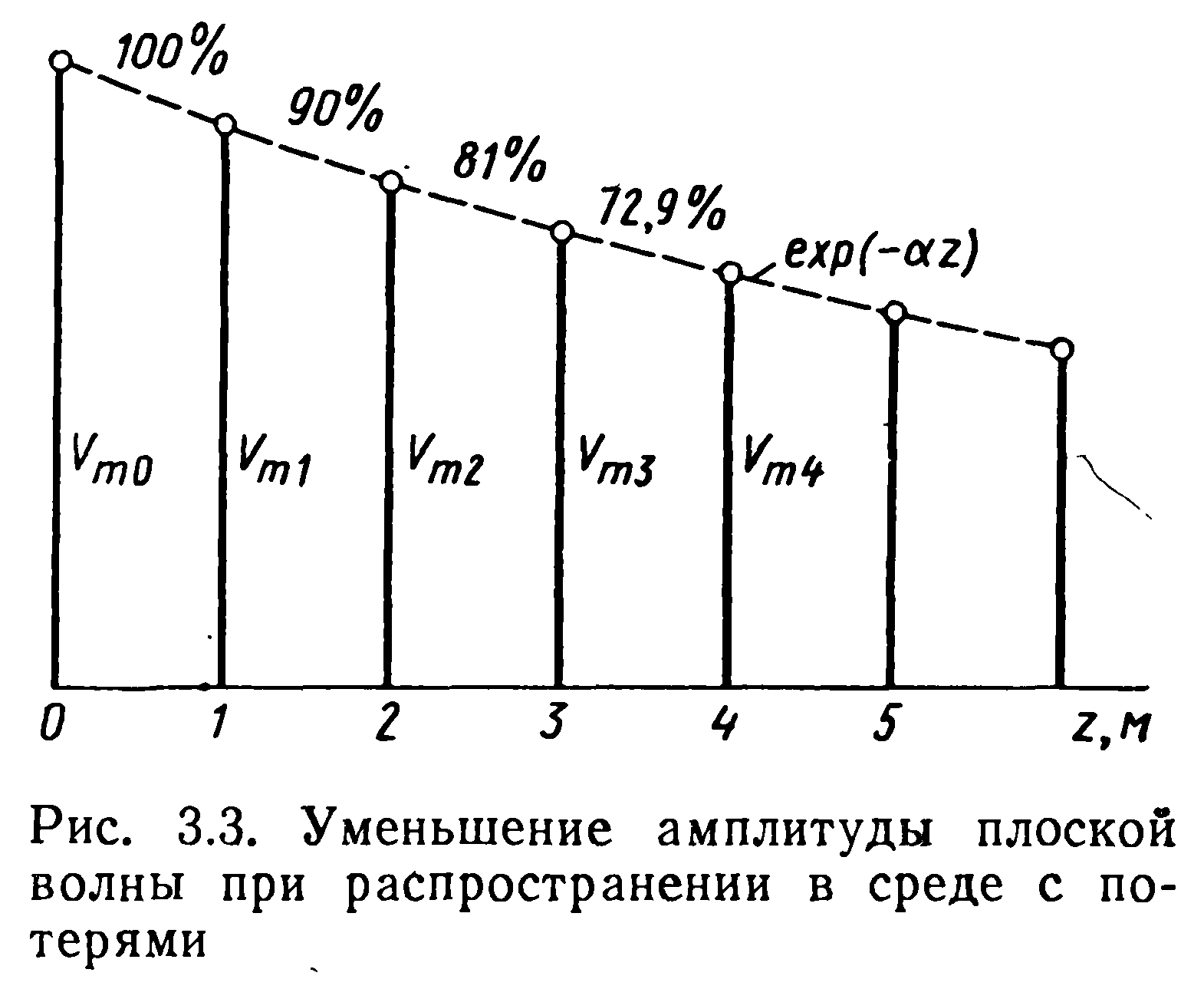
Предположим, что в начальной плоскости z=0 амплитуда имеет исходное значение Vm0 , принимаемое за 100% (рис. 3.3). Положим для конкретности, что при прохождении одного метра пути амплитуда волны уменьшается на 10%, т. е. Vm1 = 0.9Vm0 = 90%. Легко видеть, что Vm2= 0.9Vm1 = 81%, Vm3=0.9Vm2= 72.9% и т. д.
4.2 Общая закономерность такова:

Из элементарной алгебры известно, что именно таким свойством обладает показательная функция. Поэтому закон изменения амплитуды вдоль оси распространения в общем виде можно записать так:Vm(z)=Vm0exp(-αz)
где α — коэффициент ослабления плоской волны в среде. Эта действительная величина имеет, подобно коэффициенту фазы, размерность м-1. В технических расчетах часто используют особую логарифмическую единицу — погонное затухание Δпог, которое измеряют в децибелах на метр (дБ/м) и определяют по формуле : Δпог=20lg(Vm0/Vm1)=20lg(eα)=8.686α
можно записать общее выражение для пространственно-временного распределения мгновенных значений поля однородной плоской волны в среде с затуханием: V(z,t)= Vm0 e-αzcos(wt-βz)
|
3Коэффициент распространения.
Коэффициент фазы β и коэффициент ослабления α объединяют в единую комплексную величину — так называемый коэффициент распространения: γ=α+jβ
такой, что комплексная амплитуда поля плоской волны, распространяющейся в сторону возрастания координаты z , имеет вид  (+)(z)= Vm0 e-γz . Соответственно комплексная амплитуда волны, распространяющейся или, как часто говорят, бегущей в сторону уменьшения координаты z, такова: (+)(z)= Vm0 e-γz . Соответственно комплексная амплитуда волны, распространяющейся или, как часто говорят, бегущей в сторону уменьшения координаты z, такова:
 (-)(z)= Vm0 eγz .В частном случае, когда потери отсутствуют и амплитуда поля постоянна вдоль ζ, коэффициент распространения γ=jβ оказывается чисто мнимым. Возможен и другой частный случай, когда коэффициент распространения чисто действительный: γ=α При этом волновой процесс, по сути, не существует; колебания v(z, t) во всех точках пространства происходят с одной и той же фазой, отличаясь лишь амплитудами. (-)(z)= Vm0 eγz .В частном случае, когда потери отсутствуют и амплитуда поля постоянна вдоль ζ, коэффициент распространения γ=jβ оказывается чисто мнимым. Возможен и другой частный случай, когда коэффициент распространения чисто действительный: γ=α При этом волновой процесс, по сути, не существует; колебания v(z, t) во всех точках пространства происходят с одной и той же фазой, отличаясь лишь амплитудами.
8 Волновое уравнение
Любой процесс распространения волны в пространстве описывается одним и тем же дифференциальным уравнением – волновым уравнением:

Используя оператор Лапласа, волновое уравнение можно записать в виде :
 . .
Решением волнового уравнения всегда будет вол -новая функция
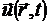 . .
Все результаты, полученные для монохроматической гармонической волны, будут справедливыми и для волн произвольной формы (сумма решений уравнения также является его решением). Поэтому далее будут исследоваться только монохроматические гармонические волны.
Коэффициент, который стоит при производной 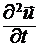 в волновом уравнении, обязательно будет обратным квадратом скорости v волны. Это скорость перемещения волнового фронта и волновых поверхностей, т.е. точек, имеющих одинаковую фазу колебаний. Поэтому скорость v называют фазовой скоростью волны. в волновом уравнении, обязательно будет обратным квадратом скорости v волны. Это скорость перемещения волнового фронта и волновых поверхностей, т.е. точек, имеющих одинаковую фазу колебаний. Поэтому скорость v называют фазовой скоростью волны.
Используя оператор Лапласа , волновое уравнение можно записать в виде , волновое уравнение можно записать в виде 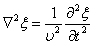
|
4 Понятие характеристического сопротивления
Рассмотрим электромагнитную волну, которая распространяется в сторону z>0 и характеризуется комплексной амплитудой  = = xexp(-γz)ix . Представив дифференциальную векторную операцию rot в развернутой форме, имеем xexp(-γz)ix . Представив дифференциальную векторную операцию rot в развернутой форме, имеем

Раскрывая символический определитель по элементам первой строки, убеждаемся, что
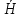 =(-jγ/ωμa)* =(-jγ/ωμa)* xexp(-γz)iy . Отсюда можно сделать ряд существенных выводов: xexp(-γz)iy . Отсюда можно сделать ряд существенных выводов:
- Если вектор Ε ориентирован вдоль оси х, то вектор Η направлен вдоль оси у, т. е. в однородной плоской волне векторы Ε и Η перпендикулярны.
6.2
- Оба вектора, Ε и Н, перпендикулярны оси распространения, поэтому однородная плоская электромагнитная волна является поперечной волной.
- Значения комплексных амплитуд векторов Ε и Η в любой точке пространства связаны некоторым коэффициентом пропорциональности.
На основании последнего из перечисленных свойств в электродинамике вводят понятие характеристического (волнового) сопротивления той физической среды, в которой распространяются однородные плоские волны. По определению, характеристическое сопротивление Zc равно отношению комплексных амплитуд соответствующих проекций векторов напряженности электрического и магнитного поля. В данном случае
Zc= x/ x/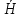 y. Так как вектор Ε имеет размерность В/м, а вектор Η — размерность А/м, то характеристическое сопротивление выражается в омах. Получаем формулу, выражающую характеристическое сопротивление через параметры среды: Zc= y. Так как вектор Ε имеет размерность В/м, а вектор Η — размерность А/м, то характеристическое сопротивление выражается в омах. Получаем формулу, выражающую характеристическое сопротивление через параметры среды: Zc=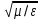 . Подчеркнем, что сопротивление Zc есть коэффициент 'пропорциональности’, не связанный в общем случае с тепловыми потерями энергии в среде. . Подчеркнем, что сопротивление Zc есть коэффициент 'пропорциональности’, не связанный в общем случае с тепловыми потерями энергии в среде.
|
5Характеристики плоских однородных электромагнитных волн, распространяющихся в реальных средах.
В качестве примеров будут исследованы характеристики однородных плоских электромагнитных волн, распространяющихся в некоторых важных для практики физических средах.
Вакуум. Данная идеальная среда имеет параметры εа=ε0, μа = μο, σ=0. Коэффициент распространения плоских волн в вакууме  оказывается мнимым, что свидетельствует об отсутствии затухания волн ( оказывается мнимым, что свидетельствует об отсутствии затухания волн ( =0).Vф=1/ =0).Vф=1/ =3*108 м/с = с- фазовая скорасть. Характеристическое сопротивление вакуума принято обозначать символом Ζ0; при этом Z0= =3*108 м/с = с- фазовая скорасть. Характеристическое сопротивление вакуума принято обозначать символом Ζ0; при этом Z0= 120π 120π 377 Ом. 377 Ом. 
Величина Z0 действительная, а это означает, что гармонические поля Ε и Η колеблются в фазе. Этот факт принято иллюстрировать, изображая пространственные распределения векторов электромагнитного поля в фиксированный момент времени (рис.3)
Отметим, что атмосферный воздух при нормальных условиях настолько схож по своим электродинамическим свойствам с вакуумом.
Магнитодиэлектрическая среда без потерь. В подобной среде относительная диэлектрическая проницаемость ε, либо относительная магнитная проницаемость μ, либо обе перечисленные величины удовлетворяют неравенствам ε>1, μ>1. Удельная проводимость σ, обусловливающая тепловые потери, равна нулю. Фазовая скорость однородных плоских волн в такой среде Vф=с/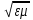 . .
Диэлектрик с малыми потерями. В радиотехнических устройствах часто используют немагнитные (μ=1) диэлектрики, угол потерь у которых весьма мал _(tg6 10-3 10-3 10-5). Приходим к следующим приближенным выражениям для коэффициента фазы и коэффициента затухания:β 10-5). Приходим к следующим приближенным выражениям для коэффициента фазы и коэффициента затухания:β и α и α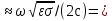 βδ/2.Итак, в диэлектрике с малыми потерями коэффициент фазы оказывается таким же, как и в диэлектрике без потерь. Согласно формулам , коэффициент затухания прямо пропорционален частоте волны, а также углу диэлектрических потерь. βδ/2.Итак, в диэлектрике с малыми потерями коэффициент фазы оказывается таким же, как и в диэлектрике без потерь. Согласно формулам , коэффициент затухания прямо пропорционален частоте волны, а также углу диэлектрических потерь.
|
6. Магнитодиэлектрическая среда без потерь
В такой среде  и (или) и (или)  удовлетворяют неравенствам: удовлетворяют неравенствам: 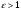 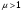  .Фазовая скорость однородных плоских волн в такой среде .Фазовая скорость однородных плоских волн в такой среде
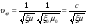 в в  раз меньше скорости распространения электромагнитных волн в вакууме. раз меньше скорости распространения электромагнитных волн в вакууме.
Характеристическое сопротивление магнитодиэлектрической среды
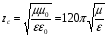 увеличивается с ростом магнитной и уменьшается с ростом диэлектрической проницаемости. увеличивается с ростом магнитной и уменьшается с ростом диэлектрической проницаемости.
9. Электромагнитные волны в средах с частотной дисперсией
Электромагнитные волны распостраниются в металлах несут потери.Амплетуда волны  убывает по экспоненциальному закону. Глубина проникновения d (скин -слой),толщина металла: убывает по экспоненциальному закону. Глубина проникновения d (скин -слой),толщина металла:
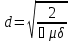 Μ-среды δ-среды Μ-среды δ-среды
Глубина проникновения электр.магн.волны в проводящую среду уменьшается с ростом частоты и удельной проводимости. Материальная среда является металлоподобной,если поле однородной волны затухает в ней на расстоянии меньше длинны волны. На Свч диапазонах величина d весьма мала.Отсюда следует что на токоведущие материалы лучше наносить тонкий слой хорошо проводящего металла,обычно серебра.
|
7. Электромагнитные волны в средах с частотной дисперсией
Электромагнитные волны распостраниются в металлах несут потери.Амплетуда волны  убывает по экспоненциальному закону. Глубина проникновения d (скин -слой),толщина металла: убывает по экспоненциальному закону. Глубина проникновения d (скин -слой),толщина металла:
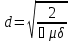 Μ-среды δ-среды Μ-среды δ-среды
Глубина проникновения электр.магн.волны в проводящую среду уменьшается с ростом частоты и удельной проводимости. Материальная среда является металлоподобной,если поле однородной волны затухает в ней на расстоянии меньше длинны волны. На Свч диапазонах величина d весьма мала.Отсюда следует что на токоведущие материалы лучше наносить тонкий слой хорошо проводящего металла,обычно серебра.
.
|
8.1 Волновое уравнение
Любой процесс распространения волны в пространстве описывается одним и тем же дифференциальным уравнением – волновым уравнением:

Используя оператор Лапласа, волновое уравнение можно записать в виде :
 . .
Решением волнового уравнения всегда будет вол -новая функция
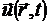 . .
Все результаты, полученные для монохроматической гармонической волны, будут справедливыми и для волн произвольной формы (сумма решений уравнения также является его решением). Поэтому далее будут исследоваться только монохроматические гармонические волны.
|
9 Распространение радиоволн в земных условиях
Земная атмосфера представляет собой пространственно-неоднородную поглощающую среду, а ее верхняя часть - ионосферная плазма обладает еще дисперсными и анизотропными свойствами. Рас�пространение радиоволн в такой среде сопровождается следующими фи�зическими процессами:
Основные физические эффекты и изучаемые явления:
влияние поверхности Земли на излучаемые волны, формирование волн, связанных с Земной поверхностью;
отражение волн от различных объектов как природных, так и искусственных, расположенных на поверхности Земли и многолучевое формирование итогового сигнала;
ослабление мощности радиоволн из-за их поглощения дождем, снегом, пылью;
отражение радиоволн от дождя, снега, пыли, стай птиц;
искривление путей распространения радиоволн из-за неоднородности слоев атмосферы.
11.2
Оценка потерь мощности сигнала при распространении радиоволн, необходимая для оценки дальности действия любой радиотехнической системы/
Многолучевое распространение радиоволн из-за постоянного изменения соотношении приводит к колебаниям мощности принимаемого сигнала, замираниям. Специалисты по теории связи изучают статистику этих замираний, конструируют аппаратуру и используют методы кодирования, адаптированные к характеру замираний.
Отражение радиоволн от разных объектов, представляет существенную помеху радиолокационным станциям, создавая ложные цели.
Искривление линии распространения радиоволн в неоднородной атмосфере ведет к ошибкам измерения координат в радиолокации и радионавигации.
Определение пространственного сектора доступности радиосредств (зона радиовидимости).
Бывают:
1)Сверхдлинные волны СДВ-мириамтр
2)Длинные волны ДВ- км
3)Средние волны-СВ-гектометровые
4)Короткие волны КВ-декаметровые
| |
|
|
 Скачать 371.08 Kb.
Скачать 371.08 Kb.