1Понятие о волнах плоские волны

Название	1Понятие о волнах плоские волны
Анкор	1-40.docx
Дата	16.06.2018
Размер	371.08 Kb.
Формат файла
Имя файла	1-40.docx
Тип	Документы #20380
страница	2 из 5

1 2 3 4 5

1 2 3 4 5
10. Волны в хорошо проводящей среде Волны в хорошо проводящих средах –металлоподобные средыФазовая скорость и длина волны в проводящей среде определяются соотношениями: δ/ϖ»ɛ - условие для хорошей проводимости в такой среде плотность токов проводимости значительно превышает плотность токов смещения и поляризационных токов,чем ниже частота ,тем проводящая среда ближе по своим электродинамическим свойствам к идеальному проводнику.Электромагнитные волны распостраниются в металлах несут потери.Амплетуда волны убывает по экспоненциальному закону. Глубина проникновения d (скин -слой),толщина металла: 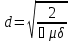Μ-среды δ-среды Глубина проникновения электр.магн.волны в проводящую среду уменьшается с ростом частоты и удельной проводимости. Материальная среда является металлоподобной,если поле однородной волны затухает в ней на расстоянии меньше длинны волны. 13.Плазма и ее электродинамические параметры. Плазма - ионизированный газ, состоящий из положительно и отрицательно заряженных частиц, а также из нейтральных атомов и молекул. Одно из основных свойств плазмы заключается в ее квазинейтральности— если в плазме мысленно выделить некоторую замкнутую область, то электрический заряд внутри нее в среднем всегда равен нулю, несмотря на то что из-за теплового движения заряженных частиц наблюдаются быстрые флуктуации суммарного заряда вокруг среднего значения. Таким образом, локальную плотность плазмы можно описывать одним параметром—электронной концентрацией Ne (м3), которая равна среднему числу электронов в единице объема. Заряженные частицы плазмы движутся под действием сил электромагнитного поля. Это приводит к поляризации среды. Рассматривая электронно-ионную плазму, следует учитывать, что масса иона на несколько порядков превышает массу электрона. Поэтому ионы практически неподвижны и в первом приближении не влияют на электродинамические свойства такой среды. Простейший способ анализа свойств плазмы основан на том, что составляют и решают дифференциальное уравнение. Уравнение, записанное на основании второго закона Ньютона, имеет вид где г — радиус-вектор отклонения электрона от того положения в пространстве, которое он занимал при отсутствии поля; е, m -заряд и масса электрона; v - так называемая частота соударений электрона с нейтральными частицами. Диэлектрическая проницаемость плазменной среды: . Физические причины – инерционность процесса, перемещение электронов плазмы под действием переменного поля	11 Распространение электромагнитных волн в бесстолкновительной плазме. Диэлектрическая проницаемость бесстолкновительной плазмы ,действительна и меньше единицы на любых частотах. Плазменная частота(или ленгмюровскай частотой) . Концентрация электронов Ne сравнительно невелика, так что выполняется неравенство. Говорят, что при этом имеет место распространение волн в докритической плазме. Параметр Ne велик настолько, что имеет место обратное неравенство. В данном случае принято говорить об электромагнитных процессах в закритической плазме. Докритическая плазма.Рис.1.Кривая, характеризующая частотную дисперсию фазовой скорости в докритической плазме, изображена на рисунке. Следует отметить, что здесь фазовая скорость плоских электромагнитных волн всегда больше скорости волн в вакууме, причем , если . Характеристическое сопротивление докритической бесстолкновительной плазмы также зависит от частоты . 14.2 Закритическая плазма. Если , то коэффициент распространения плоской электромагнитной волны в плазме оказывается действительным: . График частотной зависимости нормированного коэффициента ослабления, рассчитанный по этой формуле, изображен на рис.2. Ослабление амплитуды электромагнитных волн в закритической плазме во многих случаях оказывает существенное влияние на работу земных и космических радиолиний. Поскольку диэлектрическая проницаемость закритической плазмы отрицательна, характеристическое сопротивление подобной среды оказывается чисто мнимым: 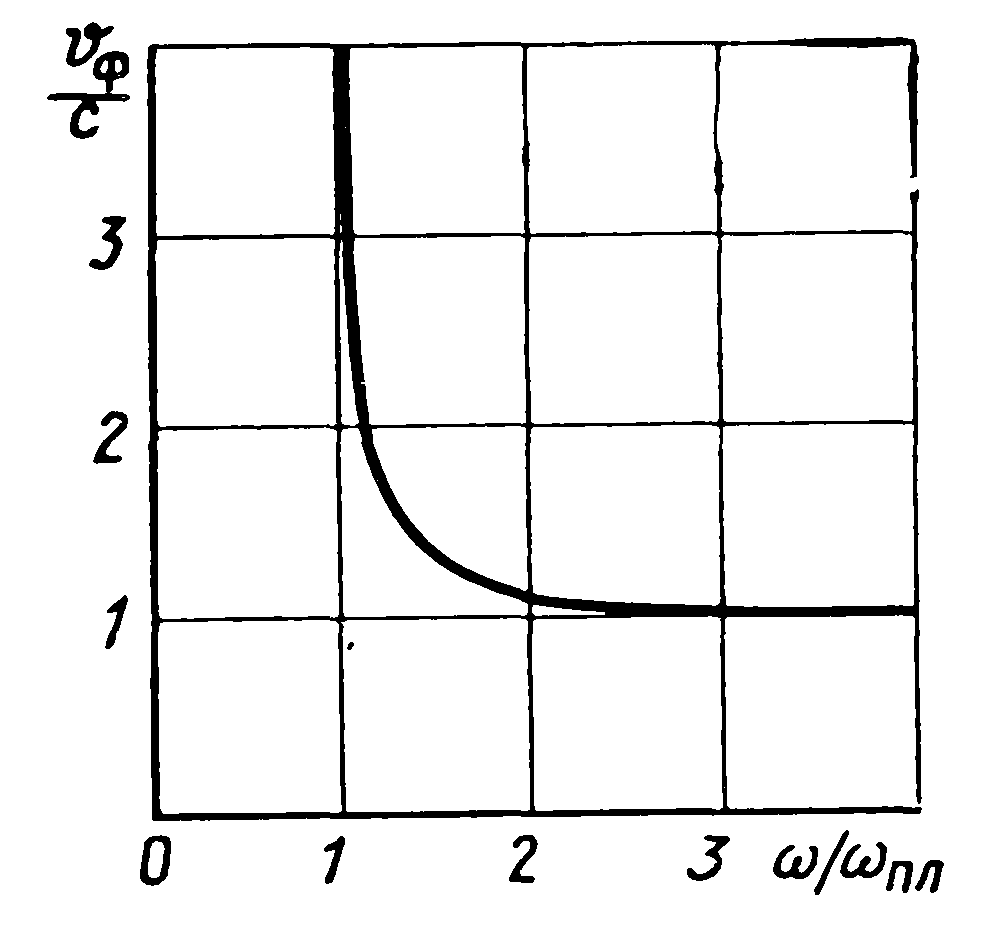. Подводя итог, можно констатировать, что слой бесстолкновительной плазмы ведет себя подобно фильтру верхних частот, пропуская на выход колебания с частотами и эффективно ослабляя спектральные составляющие с частотами .		12.Интерференция и дифракция электромагнитных волн. Интерференция – это явление сложения двух или нескольких волн, приходящих в точку приема из нескольких источников. Дифракция – явление огибания эл.магн. волнами препятствия. Если электромагнитная волна определенного вида, например плоская или сферическая, падает на объект, отличающийся электродинамическими свойствами от окружающей среды, то имеет место дифракция волны на этом объекте. Уравнению Гельмгольца где - коэффициент фазы волнового процесса при заданной частоте источника. Любое решение уравнения Гельмгольца, обладающее свойством волны, уходящей на бесконечность, должно при удовлетворять предельному условию вида: Эту формулу называют условием излучения или условием Зоммерфельда.
13 Дифракция Френеля и Фраунгофера Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Если точка наблюдения Р отстоит от излучающего раскрыва на расстоянии, исчисляемом многими длинами волн, то ,и поэтому .При анализе антенных систем обычно приходится находить поле на расстоянии , значительно превышающем размеры раскрыва . При этом угол можно считать одинаковым для всех точек раскрыва, а расстояние , равным расстоянию от точки наблюдения до центра раскрыва. Величину , входящую в аргумент экспоненциальной функции, на основании сделанных предположений можно приближенно представить следующим образом: Случай, когда оказывается справедливой эта формула, принято называть дифракцией Фраунгофера. Дифракции Френеля, или дифракции в ближней зоне. Дифракция Френеля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана. Максимальная геометрическая разность хода соответствует фазовому сдвигу между колебаниями .Рис.1.Характер распределения в ближней зоне апертурной антенны. 1-лучевая трубка; 2 - сферическая волна. Дифракция Фраунгофера имеет место в том случае, если точка наблюдения Р столь удалена от излучающей системы, что (последняя цифра во многом условна и принята для конкретности оценок). Говорят, что при этом точка наблюдения находится в дальней зоне апертурной антенны. Поле в дальней зоне имеет вид неоднородной сферической волны. Если приблизить точку наблюдения к излучающей апертуре, то максимальный фазовый сдвиг между элементарными колебаниями становится больше .При этом точка наблюдения располагается в ближней зоне антенны. Условной границей между ближней и дальней зонами служит плоскость с координатой .Анализ показывает, что для ближней зоны характерна локализация энергии электромагнитного поля в пределах «лучевой трубки» (рис.1), поперечник которой сравним с размерами апертуры. Чтобы вычислить дифракционное поле в ближней зоне, используем выражение для расстояния между точками источника и наблюдения, учитывающее квадратичные члены: .Принято говорить, что волновая картина, рассматриваемая в данном приближении, соответствует дифракции Френеля.	14.Электромагнитные волны в сверхпроводниках. Согласно модельным представлениям немецких физиков Ф. и Г. Лондонов, вещество в сверхпроводящем состоянии содержит носители заряда двух типов: нормальные носители, которые подчиняются обычным законам классической электродинамики, и сверхпроводящие носители, способные перемещаться в кристаллической решетке вещества без какого-либо сопротивления. Соответственно вектор плотности полного тока J в каждой точке сверхпроводника представляется суммой двух составляющих: , где индексы относятся к нормальной и сверхпроводящей компонентам соответственно. - лондоновская длина. - уравнение Лондонов. Согласно этому уравнению, плотность сверхпроводящего тока связана не с электрическим, а с магнитным полем.		15 Угол Брюстера.Полное внутреннее отражение. При падении плоских электромагнитных волн на границу раздела двух сред при определенных условиях коэффициент отражения может обращаться в нуль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера и обозначается как φ_Б. φ_Б удовлетворяет одному из двух уравнений: 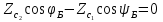(4,35) при перпендикулярной поляризации либо 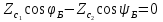(4,36) при параллельной поляризации. Здесь под ψ_Б подразумевается угол преломления, соответствующий углу падения φ_Б. Легко видеть, что уравнения (4.35) и (4.36) взаимно противоречат друг другу, т. е. явление полного преломления можно наблюдать либо при перпендикулярной, либо при параллельной поляризации. Рассмотрим наиболее часто встречающийся случай, когда обе граничащие среды являются немагнитными (µ₁=µ₂=l), в то время как оптическая плотность второй среды больше, чем первой (ε₂>ε₁). Из данных предположений, во-первых, следует что Z_с1>Z_c2. Во-вторых, в силу закона Снелля φ>ψ, т. е. cos φ Обращаясь к формулам (4.35) и (4.36), видим, что первое из этих уравнений в рамках сделанных предположений принципиально не может иметь решений. Таким образом, угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать лишь при параллельной поляризации. 21.2 Сравнение графиков, зависимостей коэффициентов отражения для волн обеих поляризаций, представленных на рис. 4.8, иллюстрирует понятие угла Брюстера.Явление полного преломления может иметь полезные технические приложения. Так, пластинка из диэлектрика, установленная под углом Брюстера по отношению к направлению распространения падающей волны, не создает отражений. В то же время эта пластинка, может играть роль важного конструктивного элемента, обеспечивая, например, вакуумное уплотнение какого-либо прибора. Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны.В оптике это явление наблюдается для широкого спектра электромагнитного излучения, включая рентгеновский диапазон.В геометрической оптике явление объясняется в рамках закона Снелла. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения, синус которого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду. В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциально затухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны. $\theta _ {\rm c} = \arcsin \!\left (\frac {n_2} {n_1} \right).$ Нарушенное полное внутреннее отражение — явление нарушения полного внутреннего отражения из-за поглощения отражающей средой части излучения. Широко применяется в лабораторной практике и оптической промышленности.
16 Замедление электромагнитных волн диэлектрической пластины. Рассматриваются электромагнитные процессы в системе, состоящей из диэлектрической пластины толщиной а, обладающей относительной диэлектрической проницаемостью ε, которая расположена на подложке из идеального проводника (рис. 11.4). Для простоты будем полагать, что диэлектрик немагнитный (µ_а = µ_а) и без потерь (σ = 0). Будет показано, что подобная пластина может играть роль волновода замедленных волн. Цель дальнейшего математического рассмотрения состоит в нахождении структуры электромагнитного поля замедленной волны, а также в определении коэффициента замедления системы. Будем решать задачу, рассматривая отдельно пространство, представляющее вакуум (область 1) и пространство внутри пластины (область 2); соответствующие индексы будут поставлены при составляющих электромагнитного поля. 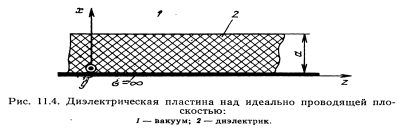Сделаем три существенных предположения: 1) рассматриваемая волна является замедленной, поэтому длина волны в волноводе удовлетворяет неравенству λ_в<λ_о, которое, будучи записанным относительно продольного волнового числа h, приобретает вид: h>γ₀; 22.2 2) система неограниченно протяженна вдоль координат z и у, указанных на рис. 11.4; 3) изучаемое поле представляет собой волну, распространяющуюся вдоль координаты z, причем магнитный вектор имеет единственную составляющую, направленную по координате у. С учетом предыдущего условия это означает, что силовые линии магнитного поля имеют вид бесконечных нитей, вытянутых над пластиной. Обратимся к рассмотрению первой области. Для составляющей Ĥ_y₁ имеем здесь уравнение Гельмгольца: 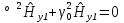(11.3) Решение этого уравнения будем искать в виде бегущей волны с неизвестными пока амплитудой и фазовой постоянной: 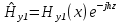(11.4) Подставляя (11.4) в (11.3) и учитывая, что по условию д/ду = 0 а также сокращая полученное выражение на общий экспоненциальный множитель, запишем обыкновенное дифференциальное уравнение 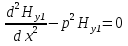где 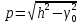, являющееся аналогом поперечного волнового числа в теории полых металлических волноводов, служит весьма важной характеристикой рассматриваемой системы. Отметим, что для замедленных волн число р всегда вещественно, поскольку h>γ_о. Общее решение уравнения (11.5) имеет вид 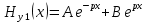где А, В — произвольные постоянные. Из физических соображений ясно, что В=0, т. К. поле не может неограниченно возрастать при удалении от направляющей системы.	17.Поверхносные электромагнитные волны. Поверхностный поляритон (ПП) - поверхностная электромагнитная волна, распространяющаяся вдоль границы раздела сред. Интенсивность такой волны быстро убывает при удалении от границы раздела сред, для линейных сред экспоненциально. На плоской границе двух изотропных сред ПП может существовать, только если хотя бы одна из пограничных сред обладает отрицательной диэлектрической или магнитнойпроницаемостью. Существуют сингулярные или бездисперсионные ПП. Они существуют на границах анизотропных кристаллов. В отличие от обычных ПП, они существуют только в определенных направлениях в плоскости границы. Изучение поверхностных поляритонов началось в связи с исследованием распространения радиоволн^[1]. Экспериментальное проявление поверхностных электромагнитных волн на границе металла обнаружено Робертом Вудом в 1912 году в виде решёточных аномалий Вуда, их интерпретация в терминах поверхностных плазмонных поляритон дана У. Фано (1941).		18 Гребенчатые и другие замедляющие волны. Система представляет собой периодическую последовательность канавок прямоугольного профиля, прорезанных в металлическом основании и ориентированных параллельно оси у. При определенных условиях в области над гребенчатой структурой может быть возбуждена поверхностная ЭМВ, которая распространяется в направлении продольной оси z. Напряженность поля этой волны с ростом поперечной координаты х уменьшается по экспоненциальному закону. Рассмотрим поле в области 2, которая представляет собой совокупность канавок, заполненных воздухом. Если ширина канавки значительно меньше длины волны, то в пределах отдельно взятой канавки поле практически неизменно вдоль координаты z. На границе раздела областей 1 и 2 касательные составляющие векторов электромагнитного поля должны быть непрерывны. Такое представление является приближенным- обусловлено малостью пространственного периода структуры по сравнению с рабочей длиной волны, вследствие чего можно не считаться с конечной толщиной металлических гребней и рассматривать всю область 2 как некоторую «искусственную среду», электродинамические свойства которой зависят лишь от соотношения между длиной волны и глубиной канавки. Обычные граничные условия, согласно которым при х = 1 касательные составляющие векторов поля должны быть непрерывны, с точностью до несущественного общего множителя можно заменить так называемым импедансным граничным условием Zпов1 —Zпов2 25.2 Поверхностный импеданс должен быть чисто реактивным и носить индуктивный характер по аналогии с известной формулой Z_L=jwL. Гребенчатая замедляющая структура не имеет диэлектрических элементов конструкции и поэтому удобна для использования в мощных электронных приборах и малогабаритных антеннах СВЧ- диапазона. Одной из первых замедляющих структур - спиральный волновод, Такой волновод представляет собой достаточно тонкий проводник, навитый на круглый цилиндр радиусом а по винтовой линии с некоторым постоянным шагом d. При возбуждении такого волновода вдоль проводника распространяется бегущая волна тока, причем скорость этой волны весьма близка к скорости света в вакууме. Коэффициент замедления равен отношению длин путей вдоль проводника и вдоль оси волновода K_зам=1/sin a. Фазовая скорость замедленной электромагнитной волны в спиральном волноводе определяется лишь геометрией спирали и не зависит от частоты. Это свойство объясняет высокую широкополосность лампы бегущей волны (ЛБВ), которая используется в качестве усилителя СВЧ-колебаний. Работа ЛБВ основана на том, что при условии синхронизма между электронным потоком и распространяющейся волной часть кинетической энергии пучка электронов может быть передана электромагнитной волне. За счет этого амплитуда колебаний на выходе прибора существенно превосходит амплитуду колебаний на входе. Очевидно, что отсутствие частотной дисперсии (зависимости фазовой скорости волн от частоты) благоприятствует работе ЛБВ в широкой полосе частот.
19. Распространение ЭМВ в анизотропной среде. Некоторые материальные среды обладают анизотропией электромагнитных свойств. Это находит отражение в том, что материальные уравнения таких сред в самом общем виде имеют следующий вид: где— тензоры абсолютной диэлектрической и абсолютной магнитной проницаемостей соответственно. В частных случаях может проявляться только электрическая или только магнитная анизотропия. Например, для магнитно-анизотропной среды абсолютная магнитная проницаемость представляет собой тензор, в то время как абсолютная диэлектрическая проницаемость является скалярной величиной. Внутренней причиной анизотропии является особенность атомно-молекулярного строения вещества, в частности упорядоченное пространственное расположение атомов в узлах кристаллической решетки. Любые монокристаллы (кварц, кремний, оксид алюминия и т. д.) анизотропны, различия состоят лишь в степени выраженности анизотропных свойств. Анизотропными становятся также аморфные вещества, помещенные в достаточно сильные постоянные электрические или магнитные поля. Изучением распространения электромагнитных волн в анизотропных средах занимаются специальные разделы физики, в частности кристаллооптика.		20 поперечное распространение радиоволн в намагниченном феррите. Рассмотрим идеализированную задачу о распространении однородной плоской электромагнитной волны в неограниченной гиротропной среде при условии, что волна распространяется в направлении, перпендикулярном вектору постоянного подмагничивающего поля Но - происходит поперечное распространение волны. Вектор Но ориентирован вдоль положительного направления оси z. Предположим, что плоская электромагнитная волна распространяется вдоль оси х, так что все проекции векторов поля имеют комплексные амплитуды, пропорциональные множителю , где— некоторый коэффициент фазы (продольное волновое число). Волновой процесс характеризуется лишь двумя комплексными амплитудами Hz и Ёу, которые удовлетворяют системе двух уравнений		21 Продольное распространение радиоволн в намагниченном феррите. Плоская электромагнитная волна распространяется в неограниченной гиротропной среде вдоль направления постоянного подмагничивающего поля. При этом все проекции векторов поля будут зависеть от продольной координаты z по закону ; выбор знака аргумента комплексной экспоненты диктуется выбором одного из двух возможных направлений движения волновых факторов. Предположим, что волны однородны в поперечной плоскости и поэтому . => находим, что т. е. рассматриваемые решения уравнений Максвелла обязательно являются чисто поперечными Т-волнами. Плоская электромагнитная волна с двумя ортогональными пространственными компонентами, сдвинутыми по фазе на угол 90°, представляет собой волну, поляризованную, по кругу. Таким образом установлено, что при продольном распространении волн в намагниченном феррите существуют две независимые моды: 28.2 1) поляризованная по кругу волна с левым направлением вращения, у которой и коэффициент фазы 2) аналогичная волна с правым направлением вращения, у ко- торой и коэффициенты фазы Теперь предположим, что в какой-либо плоскости, скажем при z=0, одновременно возбуждены обе моды с одинаковыми амплитудами. Тогда в этой плоскости комплексная амплитуда суммарного магнитного вектора ориентирована вдоль оси х и отвечает линейно поляризованной волне.
22Общие характеристики диапазонов радиоволн. 3-30Гц 105-104км КНЧ (ELF) - крайне низкие частоты Декаметрические 30-300Гц 104-103км Мегаметрические 3. 300-3000Гц 103-102км УНЧ (ULF) - ультра низкие частоты Гектокилометровые 4. 3-30кГц 100-10км ОНЧ (VLF)- очень низкие частоты Сверхдлинные (мириаметровые) 5. 30-300кГц 10-1км НЧ (LF) - низкие частоты Длинные (километровые) 6. 300-3000кГц 1000-100м СЧ (MF) - средние частоты Средние (гектометровые) 7. 3-30МГц 100-10м ВЧ (HF) - высокие частоты Короткие (декаметровые) 8. 30-300МГц 10-1м ОВЧ (VHF) - очень высокие частоты Метровые, ультра короткие 9. 300-3000МГц 100-10см УВЧ (UHF) - ультра высокие частоты Дециметровые 10. 3-30ГГц 10-1см СВЧ (SHF) - сверх высокие частоты Сантиметровые 11. 30-300ГГц 10-1мм КВЧ (EHF)- крайне высокие частоты Миллиметровые 12. 300-3000ГГц 1-0,1мм ГВЧ - гипервысокие частоты Дециметровые 13. Оптические диапазоны волн. Длиной волны называется расстояние, которое проходит волна за один временной период: l =сT=с/f , где с- скорость света, Т - период, f - частота колебания. 29.2 На первых этапах развития радиотехники связь осуществлялась с помощью волн сверхдлинного и длинного диапазонов. Недостатки: необходимость большой мощности передающего устройства из-за сильного поглощения волны при ее распространении над земной поверхностью, невозможность передавать сообщения, скорость изменения которых соизмерима со скоростью изменения несущего колебания. В радиовещании широкое применение нашли средние волны. В этом диапазоне осуществляется наиболее устойчивый прием, однако трудно обеспечить большую дальность (меньшая дифракционная способность по сравнению с более длинными волнами). Поэтому в этом диапазоне работает преимущественно местное радиовещание в зоне с радиусом в несколько сотен километров. Однако в России есть очень мощные станции этого диапазона, обслуживающие и большую территорию. Диапазон коротких волн позволяет обеспечить большую дальность действия при относительно малой мощности передатчика и направленном излучении антенны. Основным недостатком этого диапазона являются так называемые замирания - колебания уровня принимаемого сигнала, что приводит к искажению принятого сообщения. Исследования показали, что имеются оптимальные длины волн для различных часов суток и времени года. Короткие волны успешно применяют в радиовещании, радиотелеграфии на магистральных линиях связи, в морской и авиационной радионавигации. Освоение диапазонов 8-12 позволило развить такие области как телевидение и космическая связь. Благодаря распространению волн только в пределах прямой видимости и отсутствию поверхностной волны практически полностью исключены явления интеренференции волн и, следовательно, искажения сообщений. Из-за высокой несущей частоты в этих диапазонах можно разместить большое число несущих,т.е. передавать большое число различных сообщений независимо друг от друга.		23 Влияние тропосферы и ионосферы на распространение радиоволн. В окружающей земном шаре атмосфере различают две области, оказывающие влияние на распространение радиоволн: тропосферу и ионосферу. Тропосферой называется приземная область атмосферы, простирающаяся до высоты примерно 10—15 км. Тропосфера неоднородна как в вертикальном направлении, так и вдоль земной поверхности, электрические параметры меняются при изменении метеорологических условий. Тр-ра влияет на распространение земных волн и обеспечивает распространение так называемых тропосферных волн. Распространение тропосферных волн связано с рефракцией (искривлением траектории волны) в неоднородной тропосфере, а также с рассеянием и отражением радиоволн от неоднородностей тропосферы. Ионосферой наз. область атмосферы, начинающаяся от высоты 50—80 км и простирающаяся примерно до 10000 км над поверхностью Земли. В этой области плотность газа весьма мала и газ ионизирован, т. е. имеется большое число свободных электронов (примерно электронов в 1 воздуха). Присутствие свободных электронов существенно влияет на электрические свойства газа и обусловливает возможность отражения радиоволн от ионосферы. 30.2 Путем последовательного отражения от ионосферы и поверхности Земли радиоволны распространяются на очень большие расстояния (например, короткие волны могут несколько раз огибать земной шар). Ионосфера является неоднородной средой, и радиоволны рассеиваются в ней, что также обусловливает возможность распространения радиоволн на большие расстояния. Радиоволны, распространяющиеся путем отражения от ионосферы или рассеяния в ней, будем называть ионосферными волнами. На условия распространения ионосферных волн свойства земной поверхности и тропосферы влияют мало. За пределами ионосферы плотность газа и электронная плотность уменьшаются и на расстоянии, равном 3—4,5 радиусам земного шара, атмосфера Земли переходит в космическое пространство, где газ полностью ионизирован, плотность протонов равна плотности электронов .