Математика. 2. ( x )f Ф(x). Доказательство. Пусть хприращение аргумента х. Тогда по свойству 3 определенного интеграла 3

• Название: 2. ( x )f Ф(x). Доказательство. Пусть хприращение аргумента х. Тогда по свойству 3 определенного интеграла 3
• Дата: 30.05.2021
• Размер: 47.12 Kb.
• Имя файла: Математика.docx
• Тип: Документы; #211754

1. 
   1.Любая функция, ограниченная и непрерывная в некотором промежутке, является интегрируемой на этом промежутке. К классу интегрируемых функций относятся также функции, ограниченные на промежутке интегрирования и имеющие на этом промежутке конечное число точек разрыва первого рода.
   

2. 
   Если функция  f(x)  интегрируема на промежутке [a,b], то и функция  c f(x), где  c  – константа, интегрируема на этом промежутке.
   

3. 
   Если функция  f(x)  интегрируема на промежутке [a,b], то и функция | f(x) | интегрируема на этом промежутке.
   

4. 
   Если функции  f(x)  и  g(x)  интегрируемы на промежутке [a,b], то и их сумма, разность и произведение интегрируемы на этом промежутке.
   

5. 
   Если функция  f(x)  интегрируема на промежутке [a,b], то она интегрируема и в любой части этого промежутка.
   

6. 
   Если функция  f(x)  интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.
   

7. 
   Если значения интегрируемой функции изменить в конечном числе точек на конечные величины, то интегрируемость функции не нарушится.
   Применительно к функции  f(x) , которая не определена в конечном числе точек промежутка [a,b], это означает, что ни существование интеграла , ни его величина не зависят от значений, приписанных функции  f(x)  в точках ее разрыва.
   

2. ( x )f Ф(x).Доказательство. Пусть Δх–приращение аргумента х.Тогда по свойству 3 определенного интеграла

3. Формула Ньютона -Лейбница.

Определенный интеграл есть приращение первообразной функции при изменении переменной интегрирования x от a до b .

Правило: Чтобы вычислить определенный интеграл

достаточно:

1.Найти неопределенный интеграл от данной функции, положив с=0;

2. Подставив в выражение первообразной вместе аргумента x сначала верхний предел b , затем нижний предел a , из первого результата вычесть второй.

Приложения определенного интеграла.Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур

Пусть функция y=f(x) неотрицательна и непрерывна на отрезке [a, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой y=f(x) на [ a, b] численно равна определенному интегралу , т.е.

S= .

Пример. Найти площадь фигуры, ограниченной линиями

S = 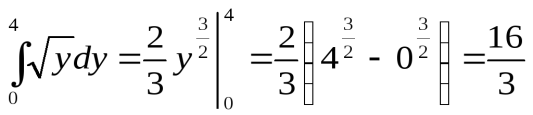(кв. ед.)

Пусть функция y=f(x) неположительна и непрерывна на отрезке [a, b]. Площадь S над кривой y=f(x) на [ a, b] отличается знаком от определенного интеграла , т.е.

S= - . (17)

Приведем формулу, применение которой упрощает решение задач на вычисление площадей плоских фигур.

Теорема. Пусть на отрезке [a, b] заданы непрерывные функции y=f₁(x) и y=f₂(x) такие, что . Тогда площадьS фигуры, заключенной между кривыми y=f₁(x) и y=f₂(x) на отрезке [ a, b] вычисляется по формуле

S= . (18)