Расчет бурового крюка. 2 часть (Бурение). 2. 1 Выбор базовой модели и технические характеристики бурового крюка
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
 2 РАСЧЕТНАЯ ЧАСТЬ 2.1 Выбор базовой модели и технические характеристики бурового крюка На основании исходных данных в курсовом проекте в качестве базовой модели выбран буровой крюк УК-225, техническая характеристика которого представлена в таблице 2.1. Таблица 2.1 ‒ Технические характеристики бурового крюка УК-225
2.2 Определение основных параметров бурового крюка Исходными данными при выборе базового крюка является конструкция скважины и проектная глубина бурения. Именно эти параметры определяют максимальную массу груза, который необходимо переместить на крюке. Исходные данные для расчета приведены в таблице 2.1. Расчет ведется по методике [7]. Нагрузка от массы кондуктора Qк, кН, определяется по формуле Qк = qк∙lк, (2.1)
Нагрузка от массы первой промежуточной колонны Q1п, кН Q1п = q1п∙l1п, (2.2)
Q1п = 0,848∙900 = 763,2 кН. Нагрузка от массы второй промежуточной колонны Q2п, кН Q2п = q2п∙l2п, (2.3)
Q2п = 0,585∙1800 = 1053 кН. Нагрузка от массы эксплуатационной колонны Qэ, кН Qэ = qэ∙lэ, (2.4)
Qэ = 0,32∙3000 = 960 кН. Нагрузка от массы бурильной колонны Qэ, кН Qб.к. = Qб.т. + QУБТ, (2.5)
Qб.т. = qб.т.∙lб.т., (2.6)
Qб.т. = 0,306. 2800 = 856,8 кН QУБТ – нагрузка от массы утяжеленных бурильных труб, кН QУБТ. = qУБТ.∙lУБТ , (2.7)
QУБТ. = 1,56∙200 = 312 кН Qб.к. = 856,8+312 = 1168,8 кН. Наибольшей является нагрузка от массы второй промежуточной колонны, поэтому максимальная нагрузка на крюке Qкр.max, кН, будет рассчитываться по формуле Qкр.max = Q2п∙К, (2.8)
Qкр.max = 1268,8∙1,2 =1368,9 кН. 2.3 Расчет деталей на прочность 2.3.1 Расчет ствола крюка на статическую прочность Ствол крюка представлен на рисунке 2.1. Сечение 1 – 1 подвержено растяжению силой Qкр.max. Напряжение в этом сечении от действия максимальной нагрузки на крюке σр, МПа, определяется по формуле 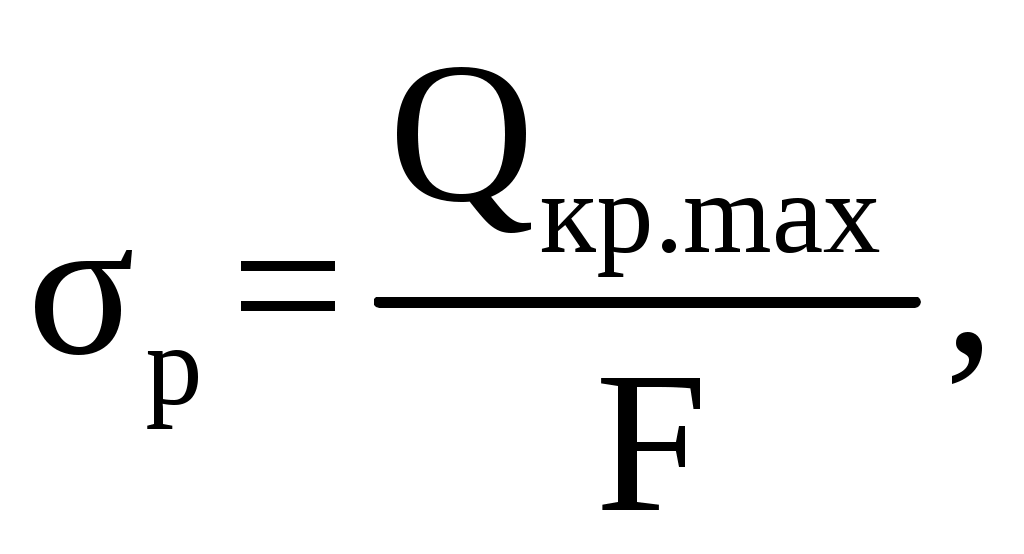 (2.9) (2.9)
 , (2.10) , (2.10)d – диаметр ствола крюка, d = 0,15 м 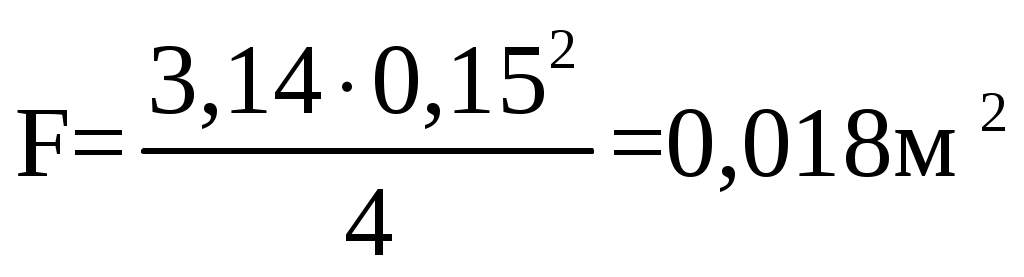 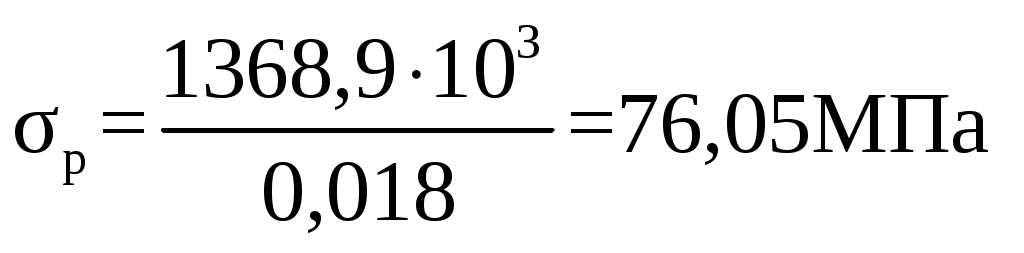 Коэффициент запаса прочности, n
Условие прочности выполняется. Сечение 2 – 2. Напряжение растяжения в сечении σр, МПа 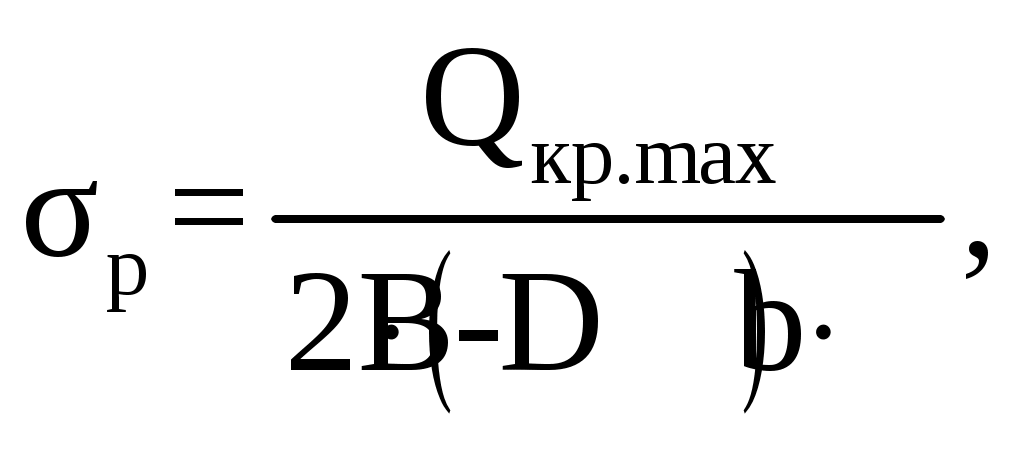 (2.12) (2.12)
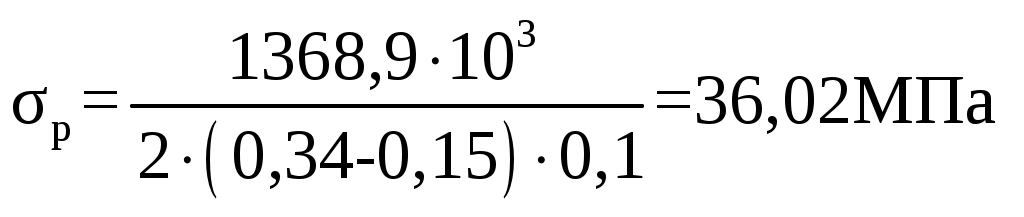 Интенсивность давления в проушинах Р, МПа  , (2.13) , (2.13) Напряжение от изгиба в сечении 4 – 4, σиз, МПа 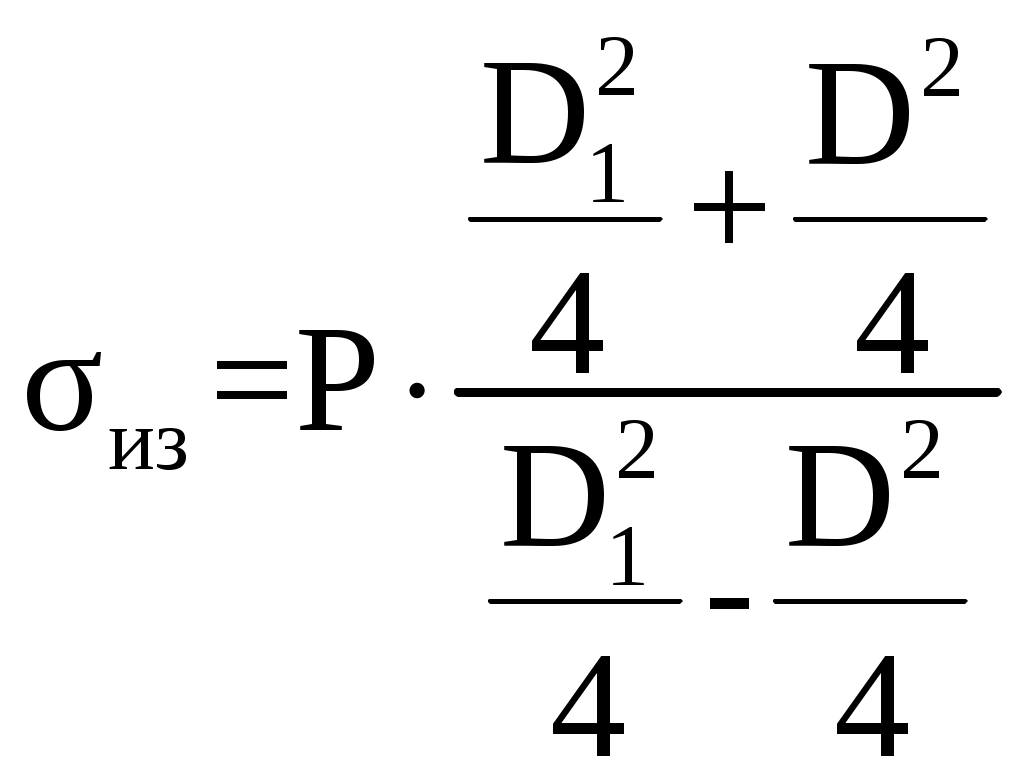 , (2.14) , (2.14)
 Коэффициент запаса прочности при изгибе, n1  , n ≥ 1,5 (2.15) , n ≥ 1,5 (2.15)Условие прочности выполняется. Коэффициент запаса прочности, n2 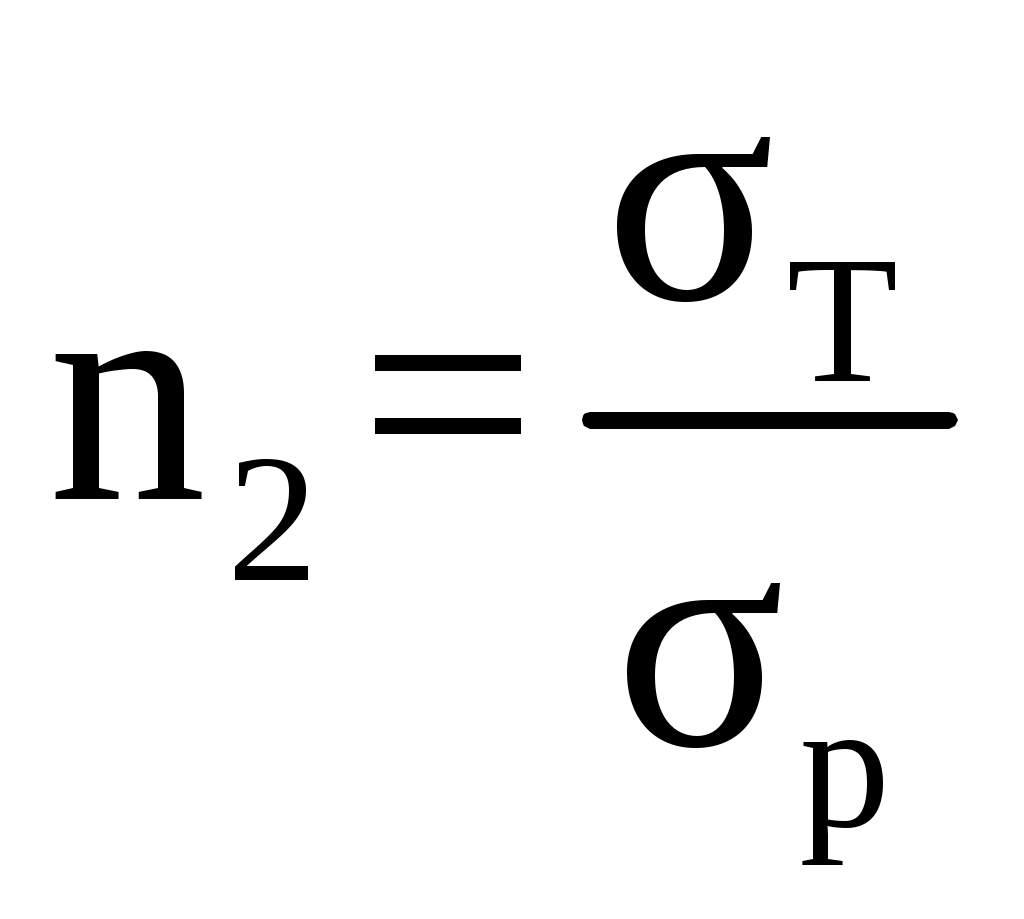 , n ≥ 1,5 (2.16) , n ≥ 1,5 (2.16)Условие прочности выполняется. Сечение 3 – 3. Резьбовая часть крюка подвержена деформациям изгиба, смятия и среза. Напряжение изгиба σиз, МПа,  , (2.17) , (2.17)
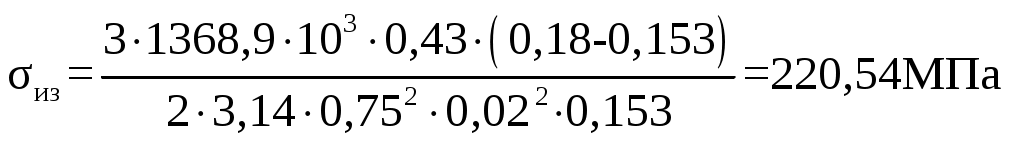 Напряжение смятия σсм, МПа 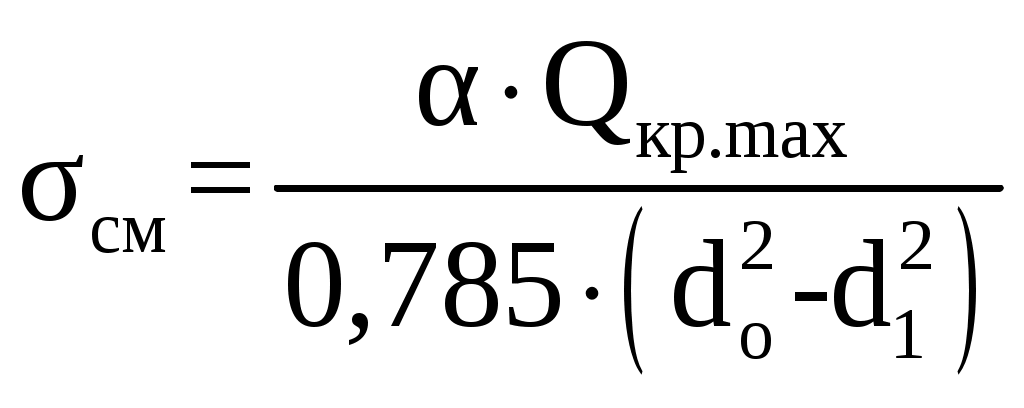 , (2.18) , (2.18) Напряжение среза σср, МПа  , (2.19) , (2.19)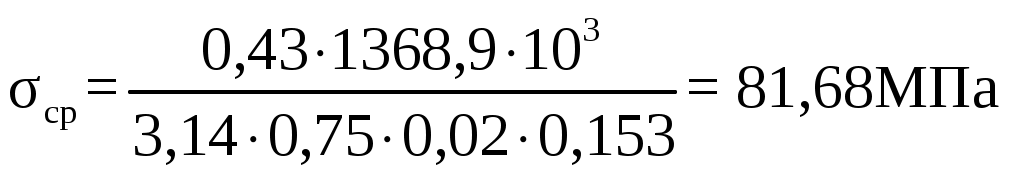 Напряжение растяжения σр, МПа
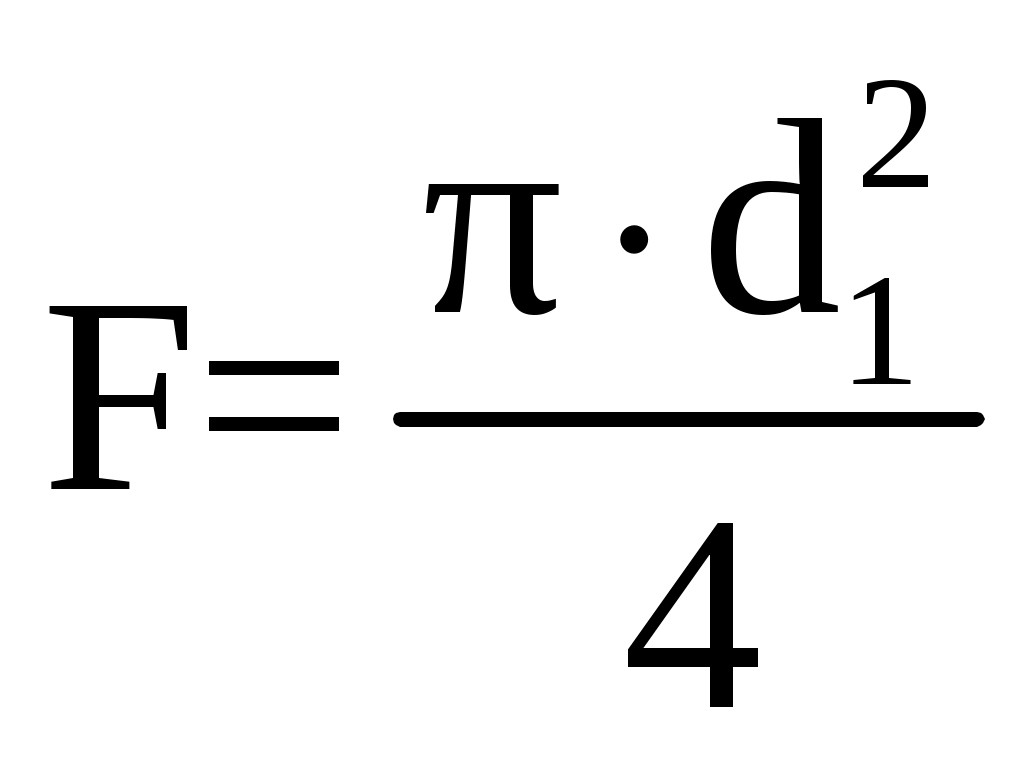 , (2.21) , (2.21)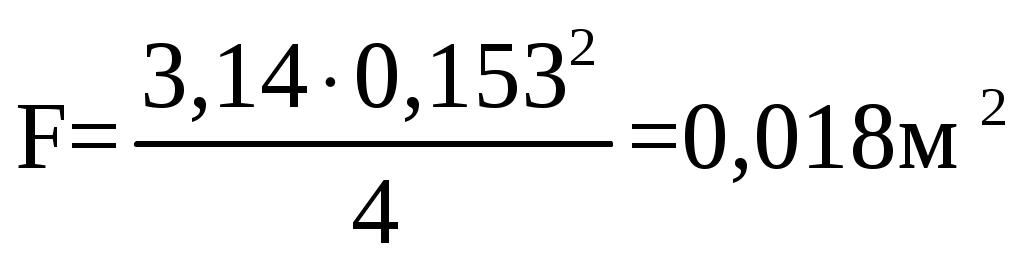 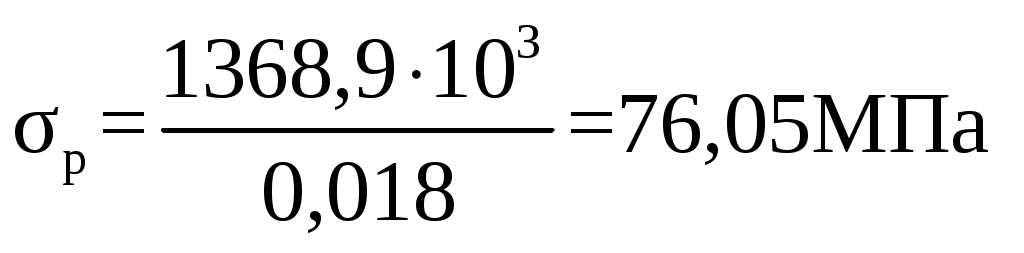 Минимальный коэффициент запаса прочности, nmin 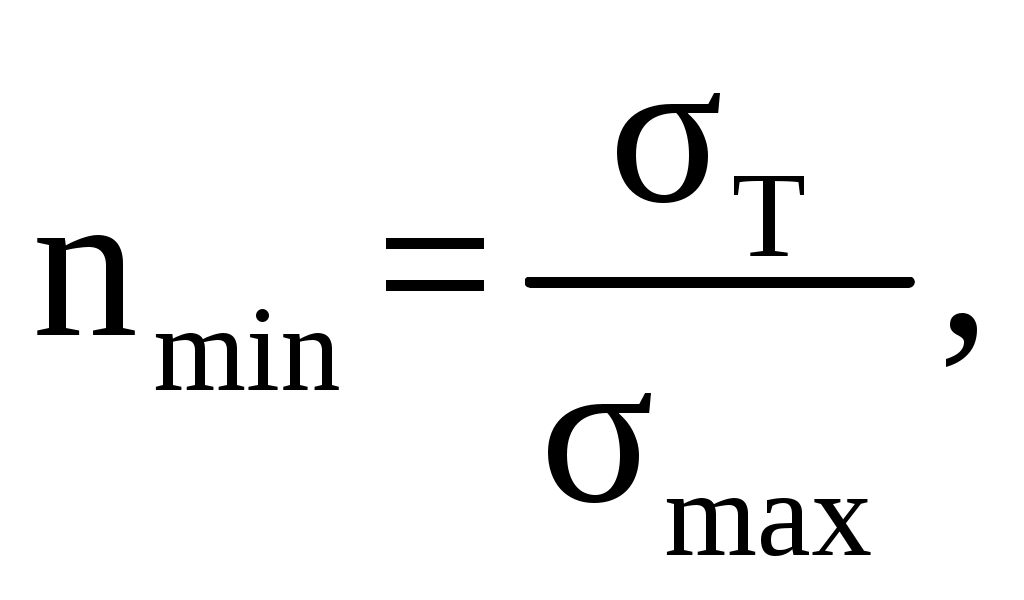 1,5 ≤ n < 1,8 (2.22) 1,5 ≤ n < 1,8 (2.22)
Условие прочности выполняется. 2.3.2 Расчет ствола крюка на усталостную прочность Расчет ведется по методике [7]. Сечение 1 – 1. Коэффициент запаса прочности, n 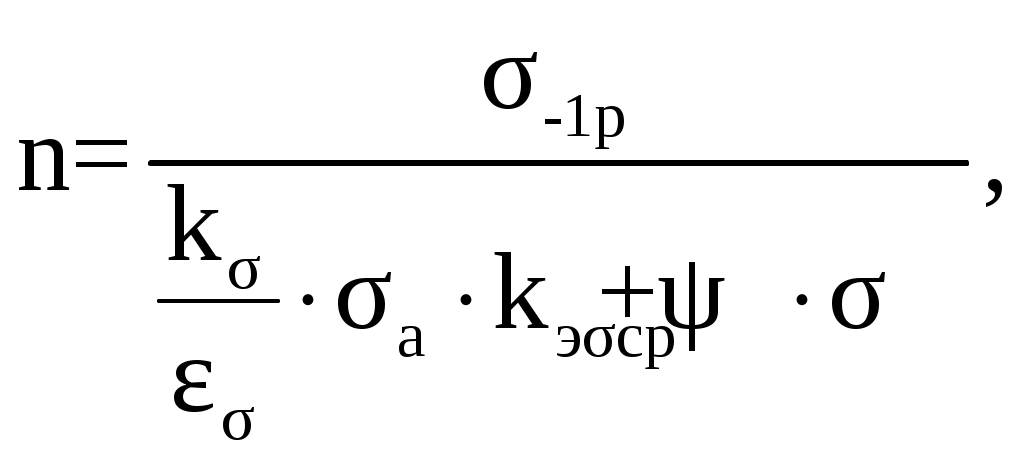 n ≥ 2 (2.23) n ≥ 2 (2.23)
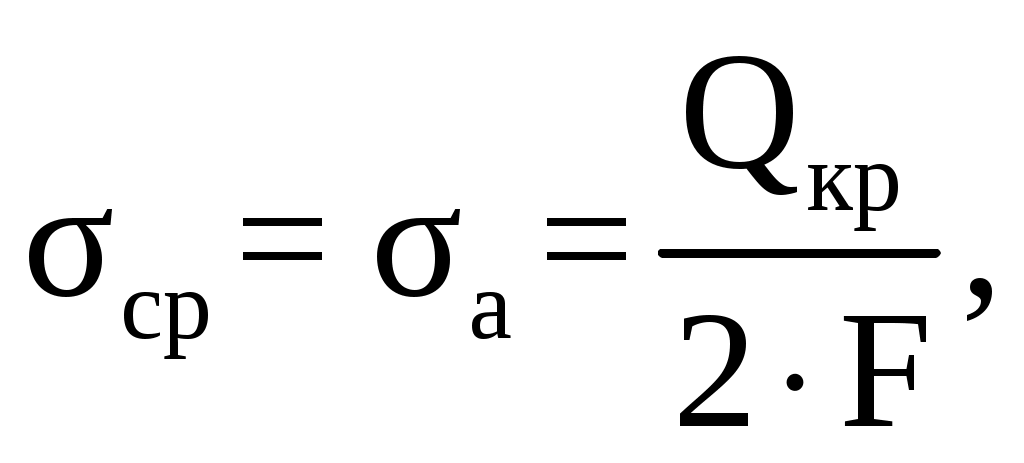 (2.24) (2.24)
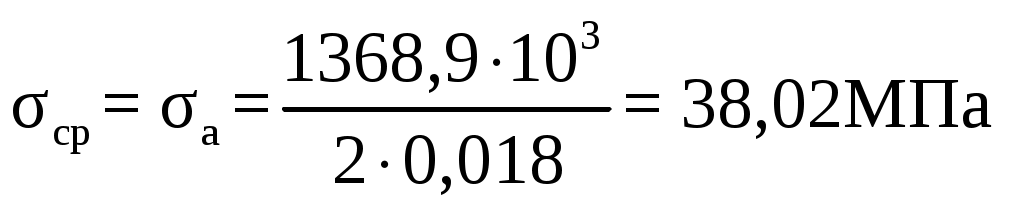
 Условие прочности выполняется. Сечение 2 – 2. Площадь сечения F, м2 F = 2∙(B-D) ∙b (2.25) F = 2∙ (0,34-0,15)∙0,1= 0,038 м2 Среднее напряжение цикла σср, МПа 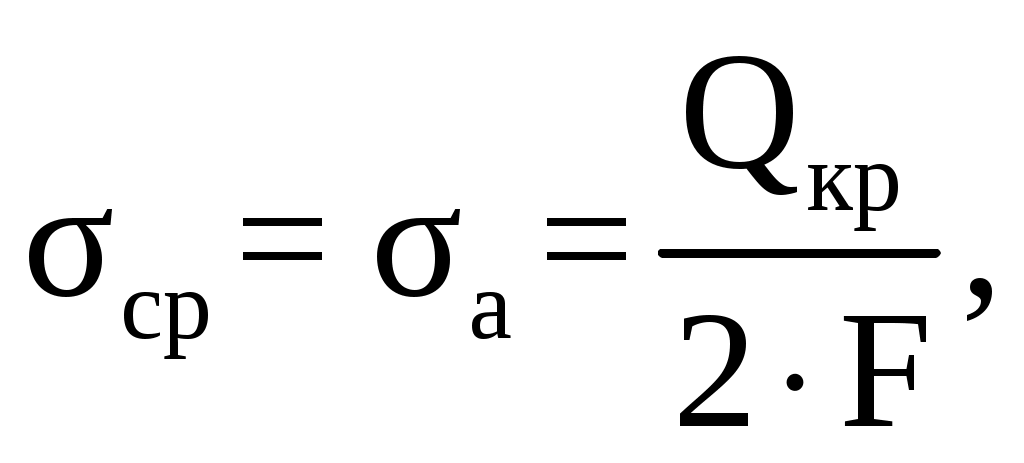 (2.26) (2.26) Коэффициент запаса прочности, n 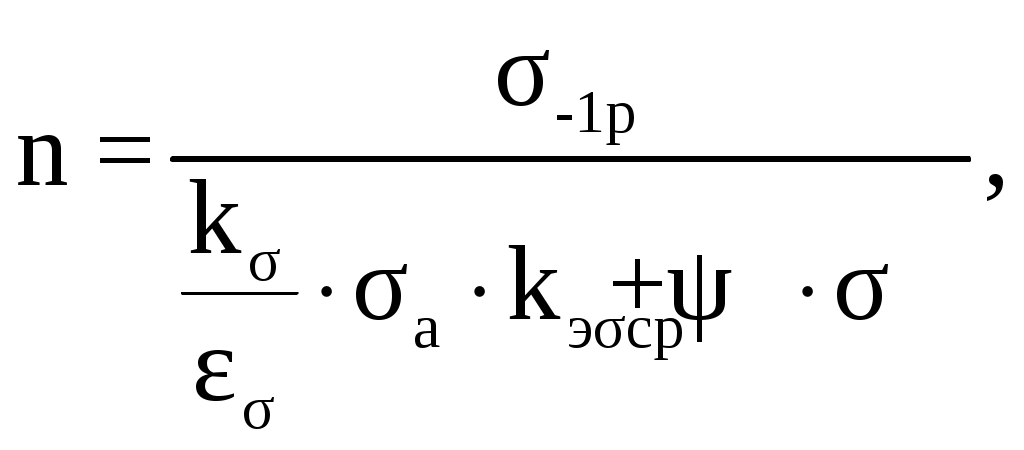 n ≥ 2 (2.27) n ≥ 2 (2.27) Условие прочности выполняется. Сечение 3 – 3. Площадь сечения F, м2 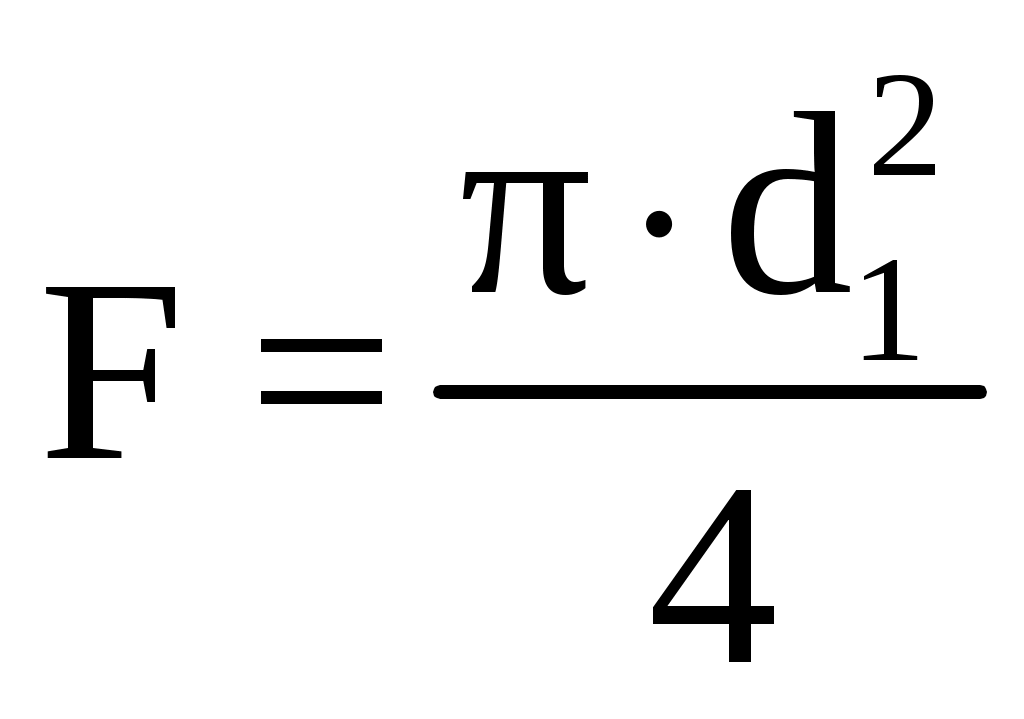 , (2.28) , (2.28)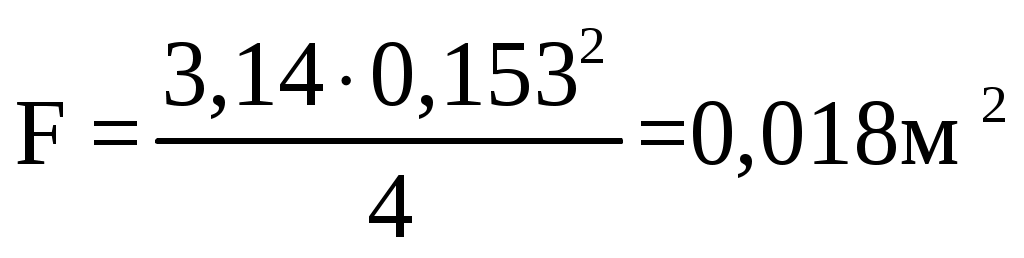 Среднее напряжение цикла σср, МПа 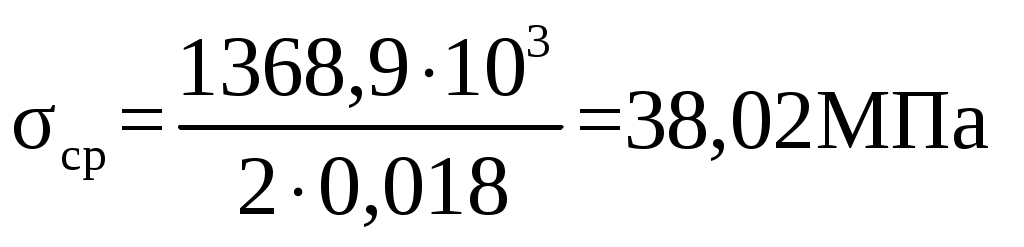 Коэффициент запаса прочности, n 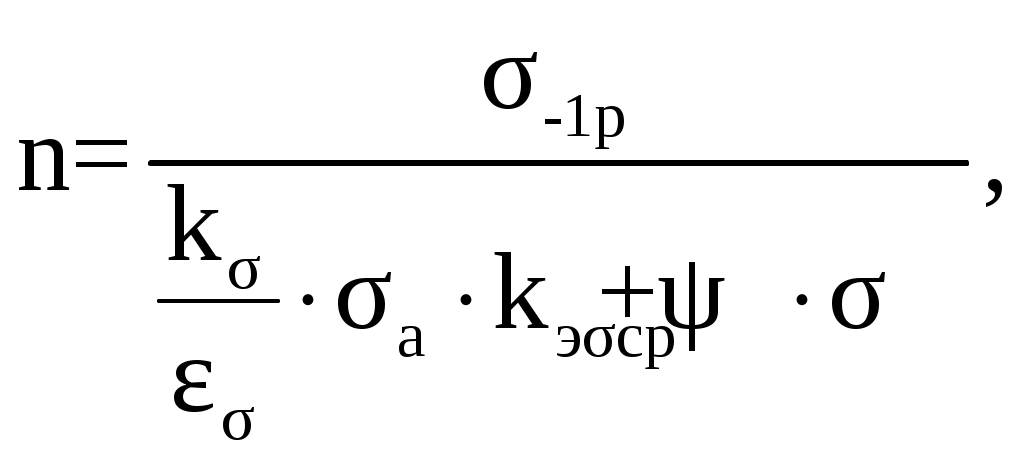 n ≥ 1,5 (2.30) n ≥ 1,5 (2.30)
 Условие прочности выполняется. 2.3.3 Расчет пластинчатого рога крюка на статическую прочность Расчет ведется по методике [7]. Рог крюка рассматриваем, как кривой брус, подверженный действию максимальной кратковременной нагрузке. Расчетная схема представлена на рисунке 2.2. Сечение 1 – 1. Вычисление нормальных напряжений требует предварительного определения положения нейтральной линии. Параметр положения нейтральной линии r, м  (2.31) (2.31)
U2 = h + U1 (2.32) U2 = 0,52 + 0,125 = 0,645 м  Центр тяжести сечения Rо, м Смещение нейтральной линии Zo, м Zo = Rо – r (2.34) Zo = 0,385 – 0,32 = 0,065 м Площадь сечения F, м2 F = B∙h, (2.35)
F = 0,125∙0,52 = 0,065 м2 Статический момент сечения S, м3 S = F∙Zo (2.36) S = 0,065∙0,065 = 0,004 м3 Расстояние центра тяжести от внутренних и наружных волокон С2 и С1, м Расстояние от нейтральной линии до внутренних волокон Z2, м Z2 = С2 – Zо (2.38) Z2 = 0,26 – 0,065 = 0,195 м Расстояние от нейтральной линии до наружных волокон Z1, м Z1 = C2 + Zo (2.39) Z1 = 0,26 + 0,065 = 0,325 м Изгибающий момент М, Н∙м, действующий в сечении 1 – 1 М = Qкр.max∙Ro (2.40) М = 1368,9∙103∙0,385 = 527026,5 Н∙м Максимальное напряжение растяжения σр, МПа 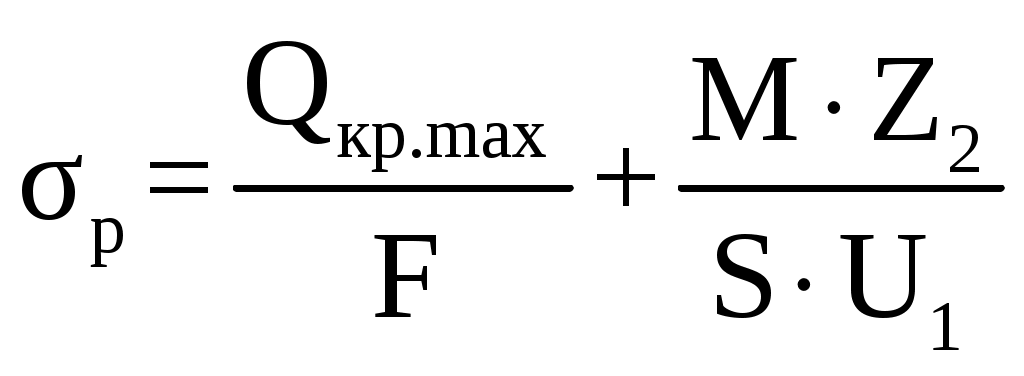 , (2.41) , (2.41)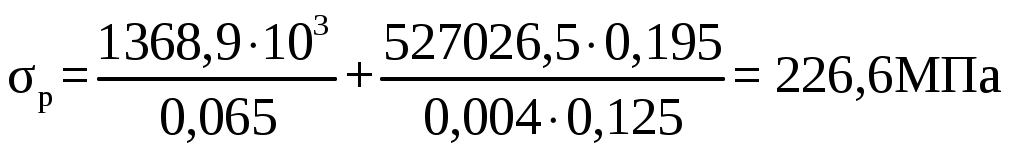 Максимальное напряжение сжатия σсж, МПа 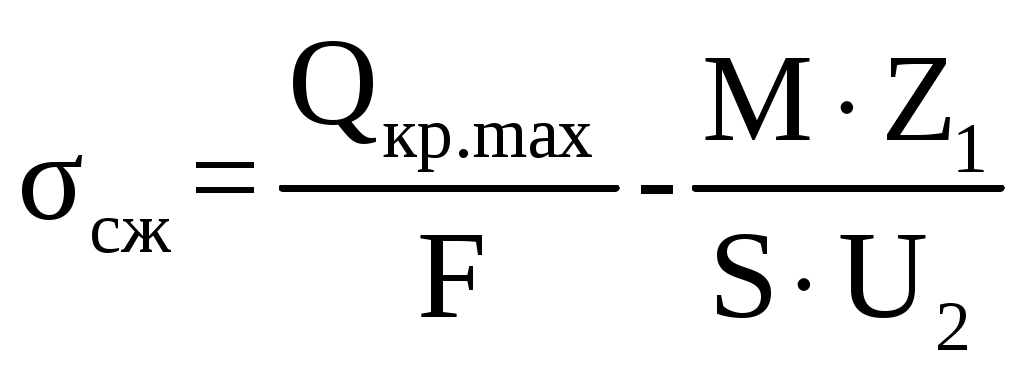 (2.42) (2.42)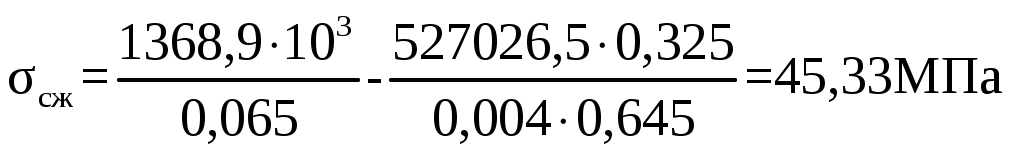 Коэффициент запаса прочности, n  n ≥ 1,5 (2.43) n ≥ 1,5 (2.43)
Условие прочности выполняется. Сечение 2 – 2. Параметр положения нейтральной линии r, м  (2.44) (2.44)
 . .Центр тяжести сечения Rо, м  (2.45) (2.45)
а = U2 – U1 (2.46) а = 0,315 – 0,125 = 0,19 м
b = U4 – U3 (2.47) b = 0,625 – 0,495 = 0,13 м  Смещение центра тяжести относительно середины сечения К, м Смещение нейтральной оси относительно центра тяжести сечения Zo, м Zo = Rо – r – К + U1 (2.49) Zo = 0,27 – 0,32 – 0,02+ 0,125 = 0,055 м. Плечо изгиба l, м 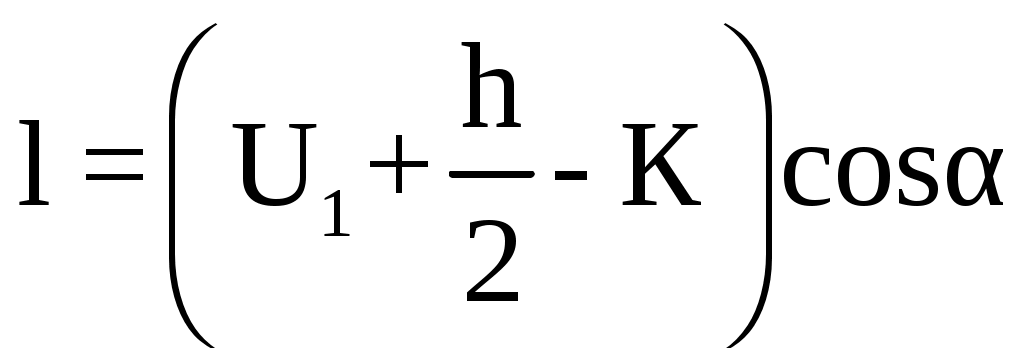 , (2.50) , (2.50)
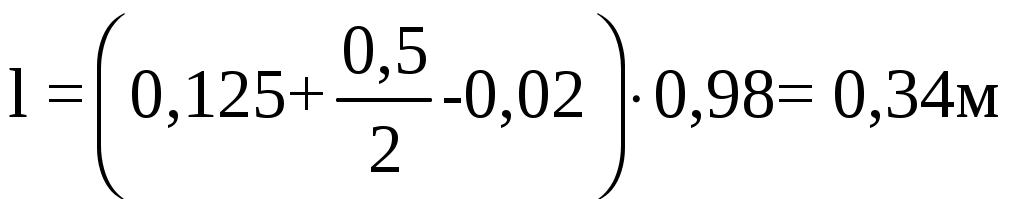 . .Площадь сечения F, м2 F = B∙(h – d), (2.51)
F = 0,125∙(0,5 – 0,17) = 0,041 м2. Статический момент сечения S, м3 S = F∙Zo (2.52) S = 0,041∙0,055 = 0,002 м3. Расстояние от нейтральной линии до внутренних волокон Z2, м Z2 = r – U1 (2.53) Z2 = 0,32 – 0,125 = 0,195 м. Расстояние от нейтральной линии до наружных волокон Z1, м Z1 = h – Z2 (2.54) Z1 = 0,5 – 0,195 = 0,305 м. Изгибающий момент М, Н∙м, действующий в сечении 2 – 2 М = Qкр.max∙l (2.55) М = 1368,9∙103∙0,34 =465426 Н∙м. Нормальная сила N, кН N = Qкр.max∙ cos α (2.56) N = 1368,9∙103∙0,98 = 1341,5 кН. Напряжение растяжения σр, МПа 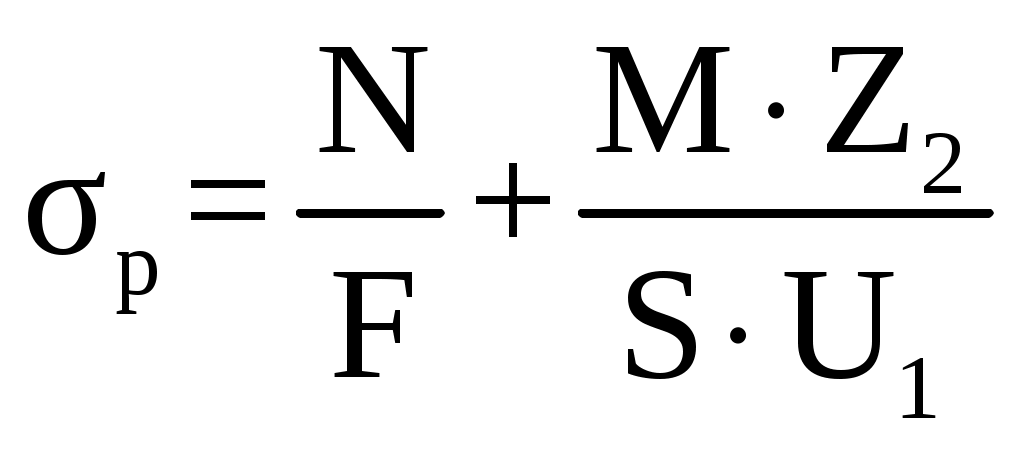 , (2.57) , (2.57)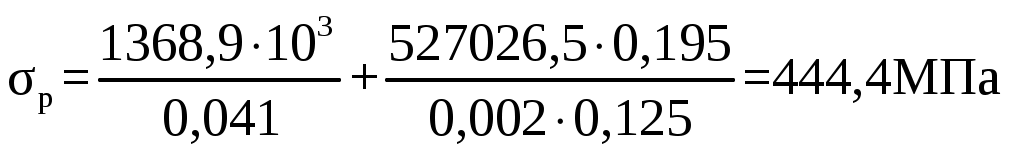 . .Напряжение сжатия σсж, МПа  , (2.58) , (2.58)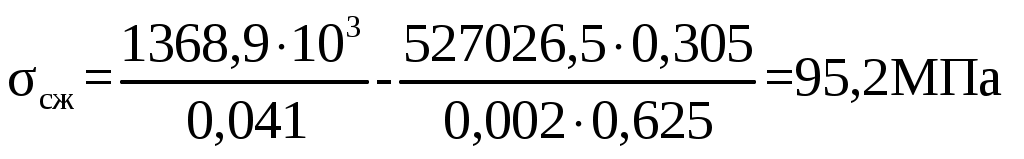 . .Коэффициент запаса прочности, n  , 1,5 ≤ n < 1,8 (2.59) , 1,5 ≤ n < 1,8 (2.59)Условие прочности выполняется. Сечение 3 – 3 подвержено действию срезывающего усилия Qкр.max. Напряжение срезывающего усилия определяется по следующему выражению σср, МПа 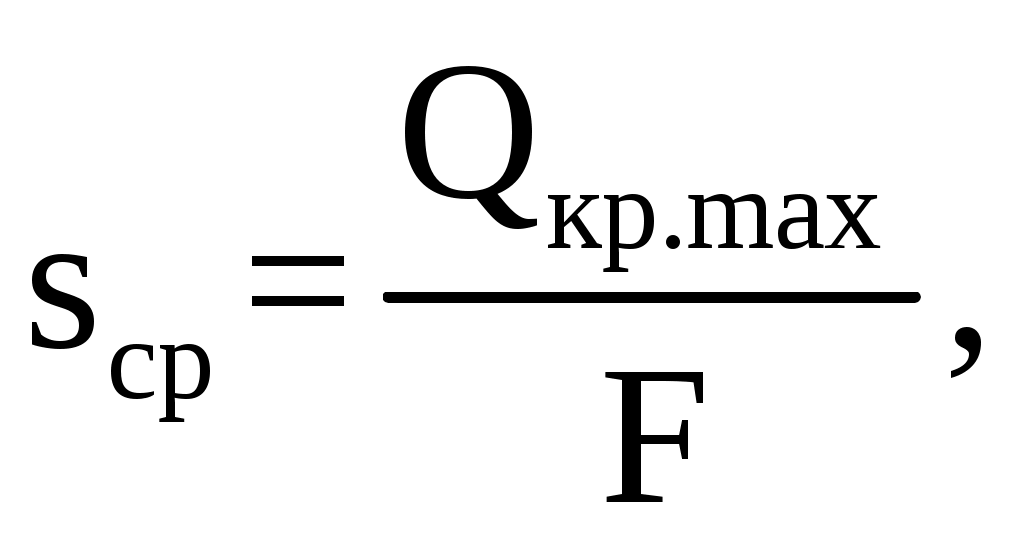 (2.60) (2.60)
F = b ∙ h, (2.61)
F = 0,12∙0,42 = 0,05 м2 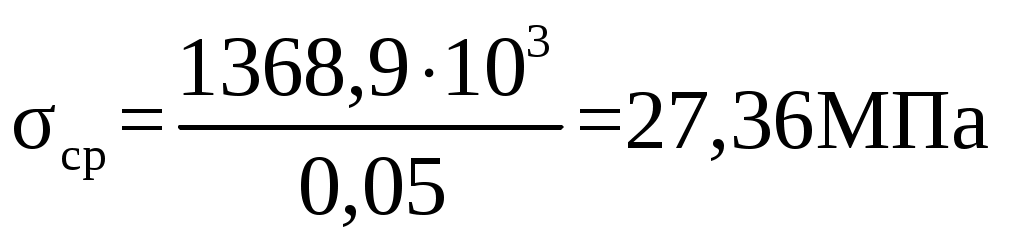 . .Сечение 4 – 4. Площадь сечения F, м2 F = 2∙b∙ (R – r), (2.62)
F = 2∙0,12∙ (0,2 –0,07) = 0,031 м2 Напряжение растяжения σр, МПа 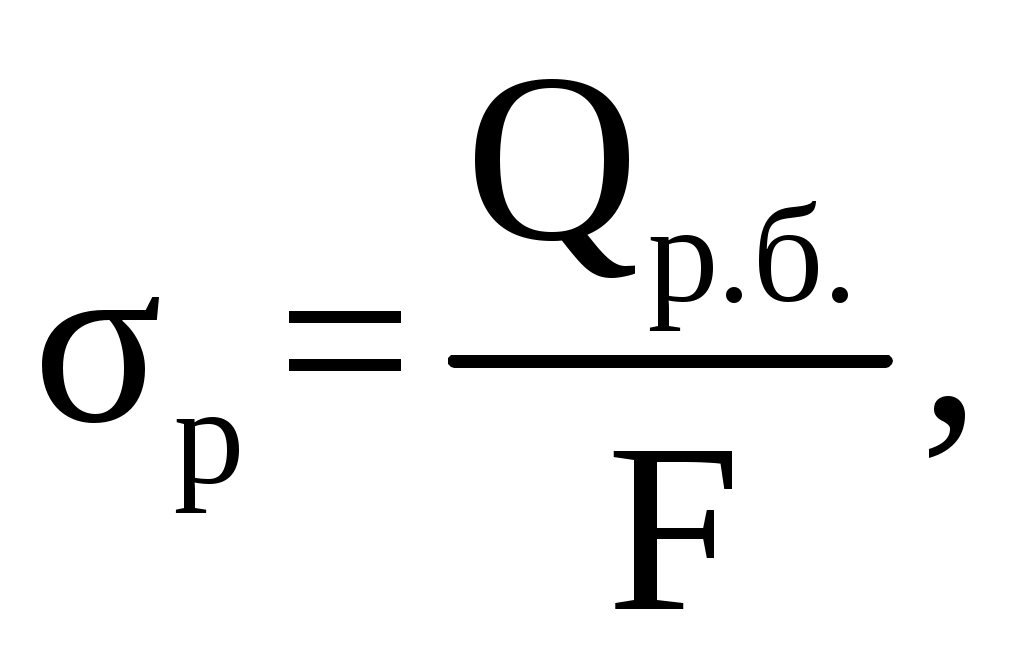 (2.63) (2.63)
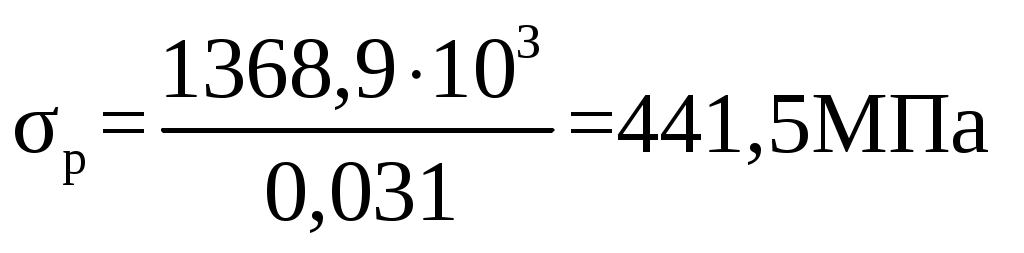 Коэффициент запаса прочности, n  , n ≥ 1,5 (2.64) , n ≥ 1,5 (2.64)Условие прочности выполняется. Сечение 5 – 5. Максимальное напряжение на внутренней поверхности проушин  , (2.65) , (2.65)
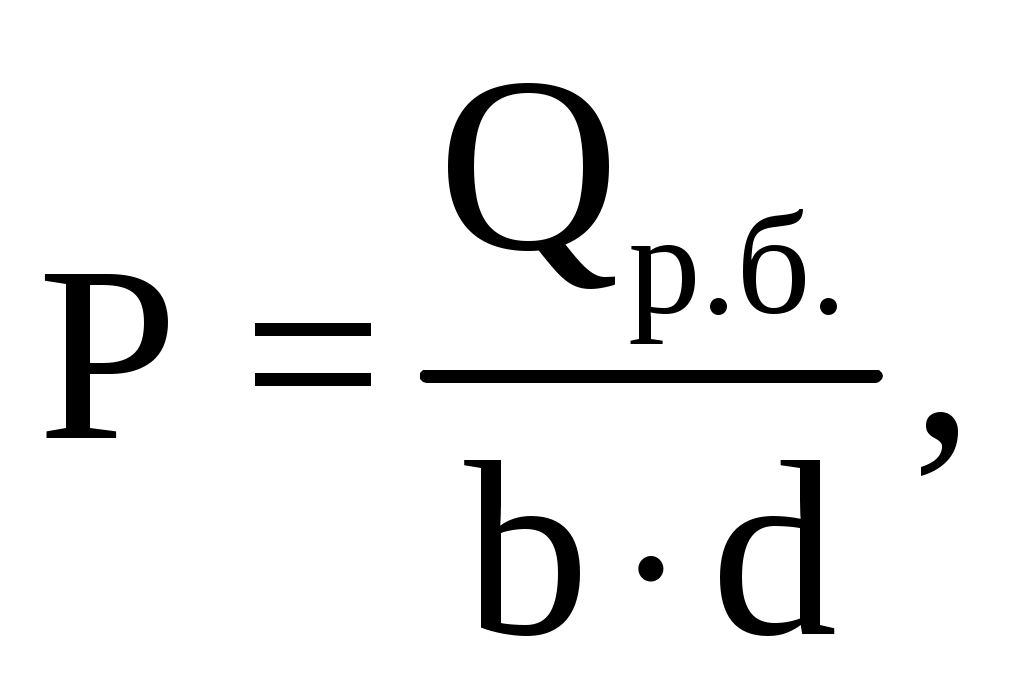 (2.66) (2.66)
d = 2∙r (2.67) d = 2∙0,07 = 0,14 м 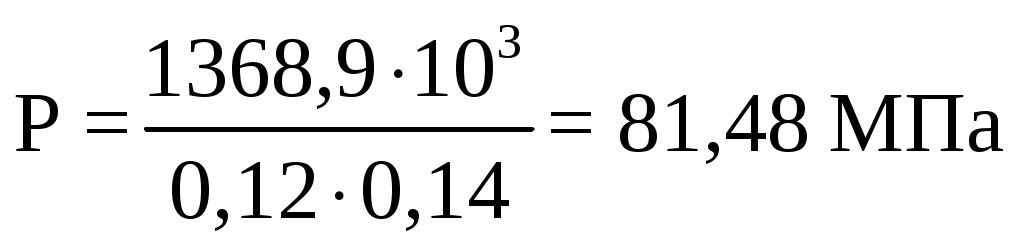 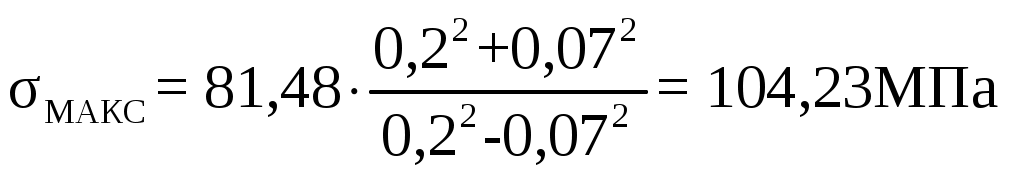 . .Минимальное напряжение на внешней поверхности проушин  , (2.68) , (2.68) . .Коэффициент запаса прочности, n 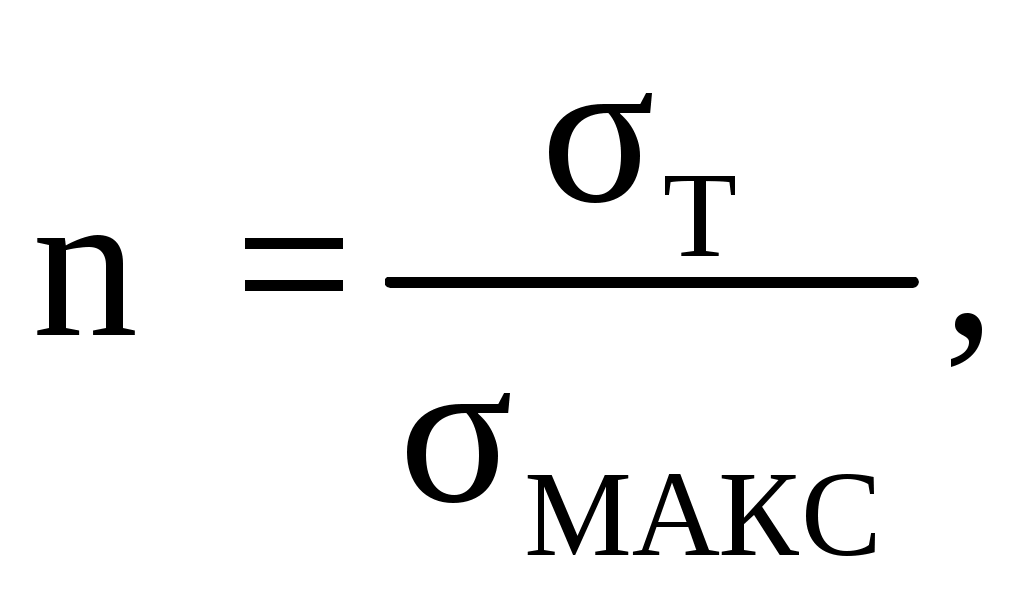 n ≥ 1,5 (2.69) n ≥ 1,5 (2.69)Условие прочности выполняется. 2.3.4 Расчет пластинчатого рога крюка на усталостную прочность Расчет ведется по методике [7]. Ввиду отсутствия источников концентрации напряжения, сечение 1 – 1 не рассчитывается. Сечение 2 – 2. Изгибающий момент М, кН∙м М = Qкр.∙l (2.70) М = 1368,9∙103∙0,34 =465426 Н∙м. Нормальная сила N, кН N = Qкр.max∙cos α (2.71) N = 1368,9∙0,98 = 1341,52 кН. Напряжение растяжения σр, МПа 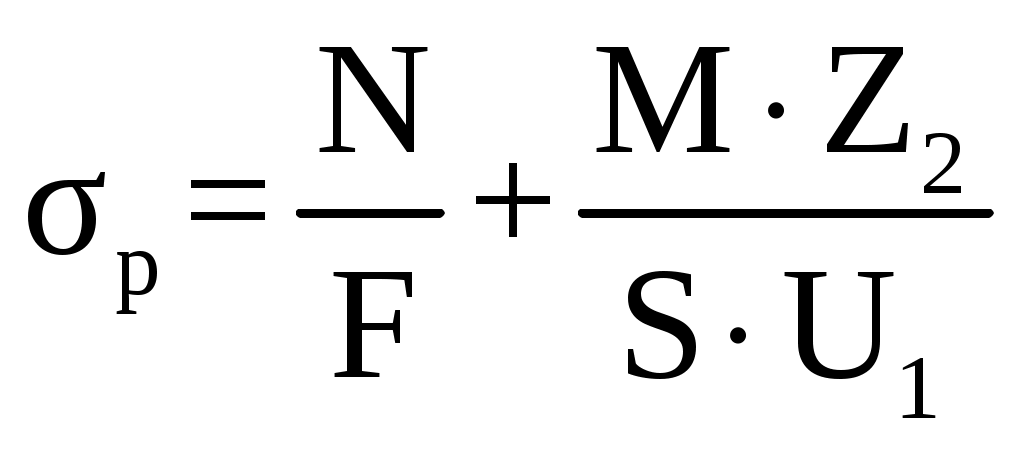 , (2.72) , (2.72) . .Площадь сечения F, м2 F = B∙(h – d), (2.73)
F = 0,125∙(0,5 – 0,17) = 0,041 м2. Амплитудное σа, МПа, и среднее σср, МПа, напряжение цикла  (2.74) (2.74)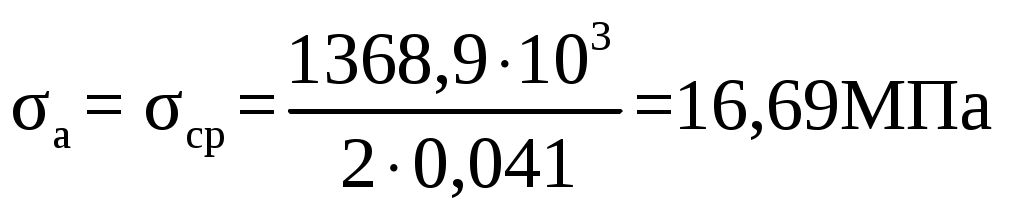 . .Коэффициент запаса прочности, n  n ≥ 2 (2.75) n ≥ 2 (2.75)
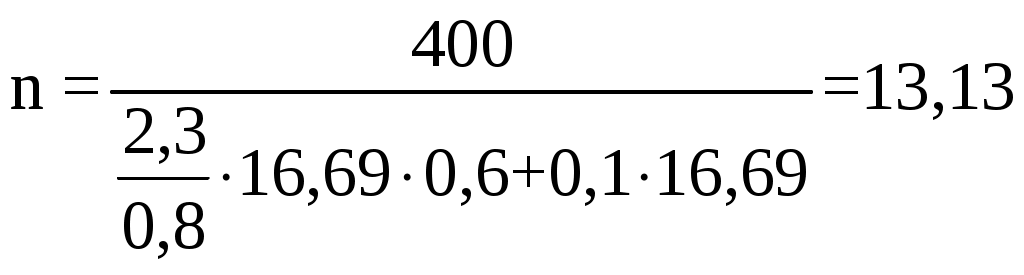 Условие прочности выполняется.  В ‒ ширина вилки; b ‒ толщина ушка вилки; D ‒ диаметр отверстия; d2 ‒ диаметр стержня ствола; d ‒ диаметр ствола Рисунок 2.1 ‒ Схема к расчету ствола крюка 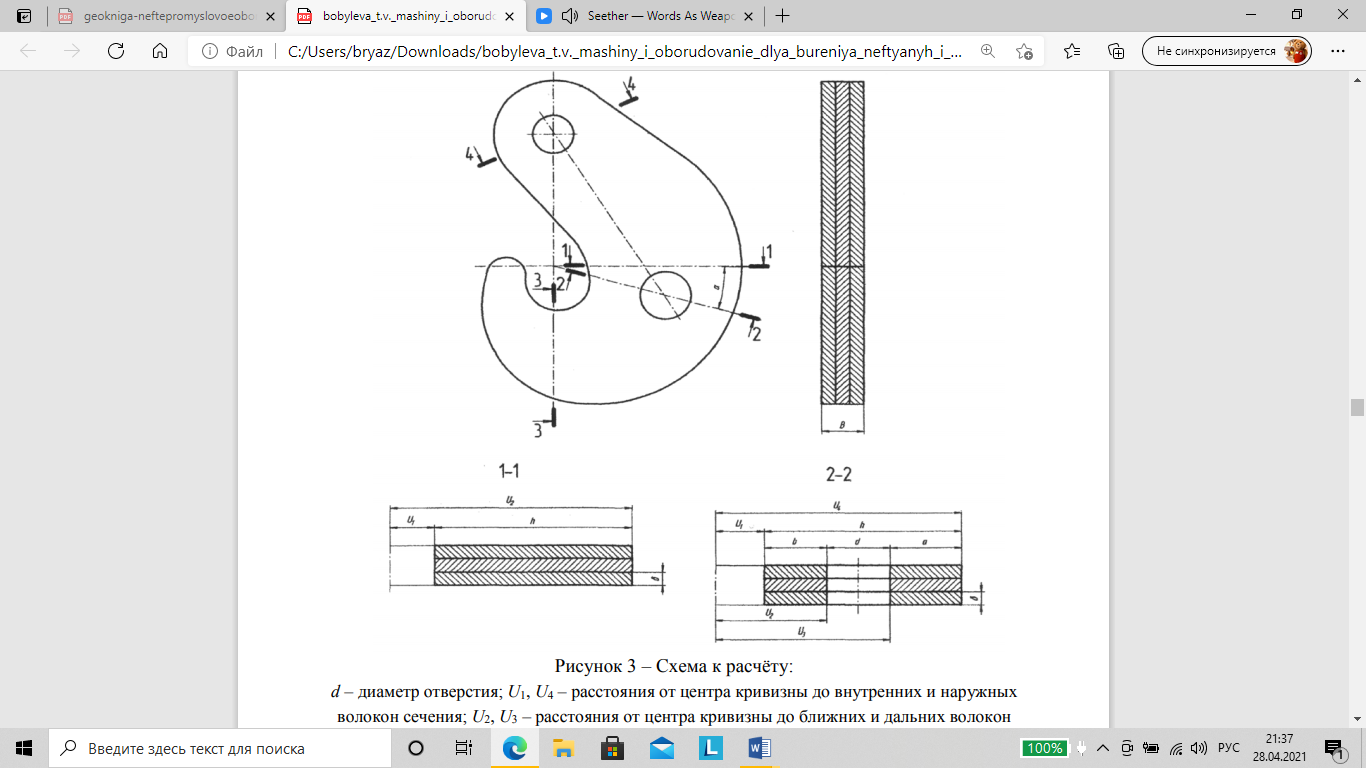 d ‒ диаметр отверстия; U1, U4 ‒ расстояния от центра кривизны до внутренних и наружных волокон сечения;U2, U3 ‒ расстояния от центра кривизны до ближних и дальних волокон отверстия; δ ‒ толщина пластины; α ‒ угол отклонения; В ‒ толщина рога; h ‒ ширина расчетного сечения; b ‒ расстояние от дальних волокон отверстия до наружных волокон сечения; a ‒ расстояние от внутренних волокон сечения до ближних волокон отверстия Рисунок 2.2 ‒ Схема к расчёту пластинчатого рога крюка
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

