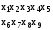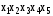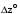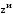Формирование плана сервисныхт улучшений.. 2. 3 Формирование портфеля проектов оптимизации итпроцессов (плана сервисных улучшений)
 Скачать 327.77 Kb. Скачать 327.77 Kb.
|
|
Согласно исходным данным первые пять проектов изменяют операционные затраты на функционирование ИТ-процессов, а последние четыре – не изменяют (  ). Положим ). Положим 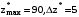 . .Результаты решения линейной задачи 1. Решив задачу (2.25) –(2.26) методом дихотомического программирования, получим следующие три лучших результата, таблица 2.17. Таблица 2.17 – Оптимальные решения задачи (2.25) –(2.26)
Результаты решения линейной задачи 2. Решив, в соответствии с предложенной схемой декомпозиции, последовательно задачи (2.31) –(2.32), (2.33) –(2.34) и (2.36) – (2.37) получим следующие три лучших результата, таблица 2.18. Таблица 2.18 – Оптимальные решения задачи (2.27) – (2.29)
Результаты решения нелинейной задачи. Положим 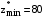 . Решив, в соответствие с предложенной выше схемой декомпозиции, задачу (2.41) – (2.42) для первых пяти проектов ( . Решив, в соответствие с предложенной выше схемой декомпозиции, задачу (2.41) – (2.42) для первых пяти проектов ( ), получим следующие результаты, таблица 2.19. ), получим следующие результаты, таблица 2.19.Таблица 2.19 - Зависимость 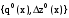 удельной эффективности удельной эффективностии изменения операционных расходов
Продолжение таблицы 2.19
Решив методом дихотомического программирования задачу (2.43) – (2.44) для последующих четырех проектов (  ), получим результаты, приведенные в таблице 2.20. ), получим результаты, приведенные в таблице 2.20.Таблица 2.20 – Зависимость 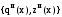 удельной эффективности удельной эффективностии изменения инвестиционных расходов
Продолжение таблицы 2.20
Формируем множество (2.45) и определяем на этом множестве оптимальные решения задачи (2.46) – (2.47), таблица 2.21. Таблица 2.21 – Оптимальные решения задачи (2.46) – (2.47)
Все четыре решения незначительно отличаются по значениям  и и  . Выбор лучшего из них следует предоставить ЛПР. Заметим, что при заданных исходных данных лучшее решение (1 0 1 0 0 1 1 1 1) нелинейной задачи (2.38) – (2.40) совпадает с лучшим решением второй линейной задачи (2.27) – (2.29) и является третьим по эффективности для первой линейной задачи (2.25) – (2.26). . Выбор лучшего из них следует предоставить ЛПР. Заметим, что при заданных исходных данных лучшее решение (1 0 1 0 0 1 1 1 1) нелинейной задачи (2.38) – (2.40) совпадает с лучшим решением второй линейной задачи (2.27) – (2.29) и является третьим по эффективности для первой линейной задачи (2.25) – (2.26). Примечание. Снятие ограничения на 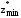 для для 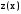 , приведет к выбору в качестве оптимального решения, приведенного таблиц 2.22. , приведет к выбору в качестве оптимального решения, приведенного таблиц 2.22.Таблица 2.22 – Оптимальное решение задачи (2.46) – (2.47) при отсутствии ограничения 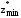
Это решение, несмотря на существенно лучшее значения критерия, неприемлемо, так как использует только 30% инвестиционного бюджета. |