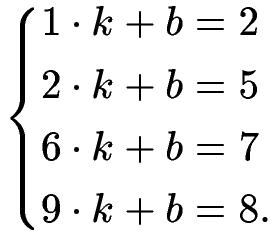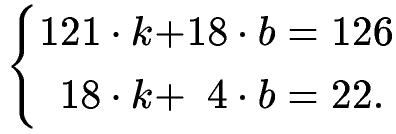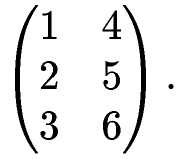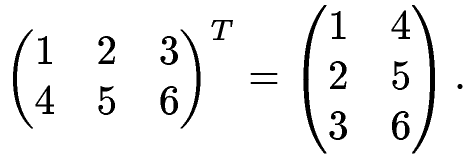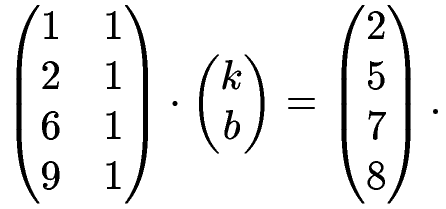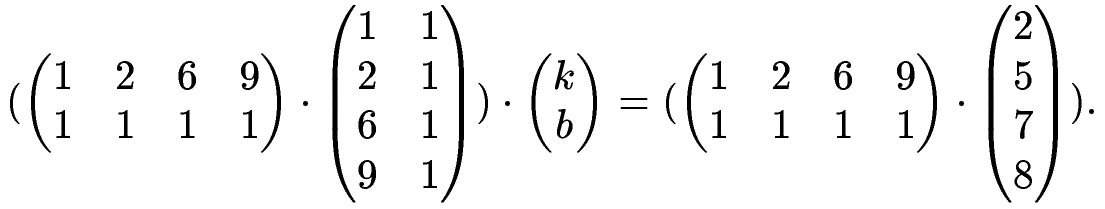математика поготовка к тесту. математика подготовка к тесту (1). 2. 3 Матрицы и метод наименьших квадратов

Название	2. 3 Матрицы и метод наименьших квадратов
Анкор	математика поготовка к тесту
Дата	30.03.2022
Размер	83.21 Kb.
Формат файла
Имя файла	математика подготовка к тесту (1).docx
Тип	Решение #428990

2.3 Матрицы и метод наименьших квадратов

Выше вы узнали, что матрицы нужны для простой записи сложных формул. Сейчас вы узнаете пример такой формулы.

Как известно, не у всех систем линейных уравнений есть решение. Но что делать, если решения нет, а найти его очень хочется? Такое странное желание возникает естественным образом при обработке не очень точных данных. Как известно, через любые две точки проходит прямая, и вы знаете, что для её нахождения нужно решать систему линейных уравнений (как это делалось в примере 7).

Предположим, координаты точки - результат некоторого измерения и этих точек не две а три или больше. Если все измерения идеально точны (как на рисунке 1), то можно сделать как раньше, и у вас получится система из более чем двух уравнений с двумя неизвестными и у неё будет решение.

Но что, если из за ошибок измерения эти точки не лежат на одной прямой (как на рисунке 2, например)?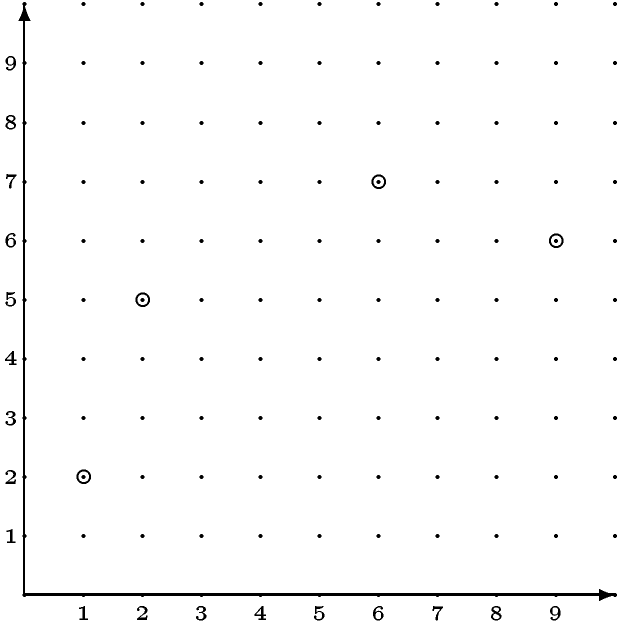

Рис. 3: Точки не на прямой

В "реальной жизни" выход есть - нужно провести прямую не через точки, а близко от точек (как на рисунке 3).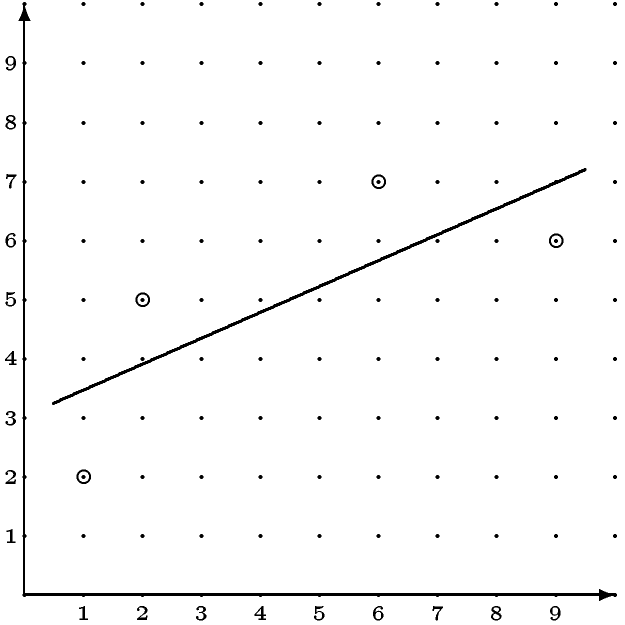

Рис. 4: Прямая вблизи точек

Человеческий мозг - штука мощная, и с этим легко справляется, но как это запрограммировать?

Если попытаться просто действовать так, как будто точки лежат на одной прямой, (т.е. как в примере 7) то, вы получите систему у которой нет решения (т.к. точки не лежат на одной прямой), но которую очень хочется решить.

(8)

Напомним, что решение системы уравнений - это числа, которые после подстановки в уравнения вместо неизвестных превращают все уравнения в верные равенства. Мы будем искать псевдорешение - числа, которые после подстановки превращают уравнения в почти верные равенства.

Например, посмотрев на рисунок 3, и определив "на глаз" уравнение прямой:

y ≈ 0.4·x + 3 ,

можно обнаружить, что числа k ≈ 0.4 и b ≈ 3, после подстановки в систему (8), дадут те самые почти верные равенства.

Упражнение 7 Подставьте и проверьте.

В этот момент у вас должно возникнуть два вопроса:

Что значит "почти" и "близко"?
При чем тут "наименьшие квадраты" и почему нет "наибольших ромбов" например?

Любопытные могут погуглить Википедию, а мы ~~трусливо~~ смело проигнорируем эти и остальные вопросы и перейдем сразу к алгоритму решения:

Заменяем систему без решения на другую, улучшенную систему, у которой решение уже есть.
Решение улучшенной системы и будет псевдорешением первой (той, у которой нет решения).

Например, систему (8) заменим на

(9)

(Почему именно на неё, написано ниже, в примере 15). Её решением как раз и будут k=18/41 ≈ 0.439024 и b=124/41 ≈ 3.02439. И та самая линия на рисунке 3 задается уравнением

y = 0.439024·x + 3.02439 .

Для реализации алгоритма понадобятся "формулы", превращающие числа из исходной системы в числа в улучшенной системе, и вот эти формулы как раз легко записать "через матрицы". Но сначала нам понадобится одно техническое понятие:

2.3.1 Транспонирование матриц

Транспонирование - это как бы переворачивание матрицы через главную диагональ.

Пример 14 Исходная матрица:

транспонированная матрица:

Как видите, при транспонировании строчки превращаются в столбцы, а столбцы в строчки.

Обозначается транспонирование A^T, т.е.³

Итак , продолжим излагать

2.3.2 Алгоритм улучшения систем линейных уравнений

Берем систему уравнений, записываем в матричном виде (как это сделано в примере 13) и получаем матричное уравнение вида

A·X=Y .
Умножаем обе части матричного уравнения на транспонированную A слева:

A^T·A·X = A^T·Y
и получаем новое матричное уравнение.

(A^T·A) ·X = (A^T·Y) .
Записав его обратно в виде системы уравнений, получим то, что нам и нужно - "улучшенную систему".

Пример 15 Система уравнений (8) в матричном виде выглядит так:

После умножения на транспонированную получится:

Умножив и записав в виде системы уравнений, получим систему (9) .

2.4.4 Экономическая модель Леонтьева

Сейчас мы расскажем вам то, за что дали Нобелевскую премию (но это не точно).

Представьте себе остров Чунга-чанга, на котором выращивают кокосы и бананы. Местные Чунгачанговцы часть кокосов и бананов съедают сами, остальное отдают своим заокеанским хозяевам.

Предположим для определенности, что при выращивании тонны кокосов они съедают 100 килограмм кокосов и 300 килограмм бананов. При выращивании тонны бананов - 200 килограмм кокосов и 600 килограмм бананов.

Постановка задачи такая: Какой урожай следует запланировать, чтобы вывезти с острова 60 тонн кокосов и 60 тонн бананов?

Для решения введем обозначения: U - таблица с урожаем, X - таблица со съеденным продуктом и V - таблица с вывезенным продуктом. В нашем случае

Тут, под первым номером идут кокосы, а под вторым бананы. (Понятно. что если бы выращивали не только кокосы и бананы, а еще и кукурузу и помидоры, то в таблице было бы больше двух чисел).

Между выращенным и съеденным есть очевидная зависимость:

Действительно, т.к. при выращивании 1 тонны кокосов съедается 100 кг = 0.1 тонна кокосов, то при выращивании u₁ кокосов съестся u₁ ·0.1 кокосов. Аналогично с бананами, на u₂ бананов съестся u₂ ·0.2 кокосов. Осталось сложить съеденные кокосы, и получится первое уравнение. Второе получается аналогично.

Между выращенным, съеденным и вывезенным есть очевидная зависимость:

Действительно, т.к. всё что не съели то вывезли.

Эти зависимости можно записать в матричном виде:

X = A·U и U=V+X ,

(11)

где

(Кстати, если продуктов не два, а много-много, то зависимости в матричном виде будут те же самые. Вот какие матрицы полезные).

Итак, наша цель - научиться находить запланированный урожай, т.е. U.

Уравнения (11) очень простые, если бы они были "про числа", то вы бы легко выразили U через V. С матрицами это так же просто, но нужно не забывать, что роль 1 теперь играет единичная матрица E:

(E−A)·U = V или U=(E−A)⁻¹ ·V

Осталось найти обратную матрицу и умножить.

Упражнение 15 Погуглите "обратная матрица онлайн", найдите ту самую обратную матрицу и узнайте, какой урожай надо запланировать для вывоза с острова 60 тонн кокосов и 60 тонн бананов.

Ответ:

Урожай должен быть: 120 тонн кокосов и 240 тонн бананов.

2.5 Как искать обратную матрицу

Оказывается , для обратной матрицы есть готовая формула. Очень удобно, подставляем в нее числа из матрицы, вычисляем по формулам, и готово. Для матриц размера 2×2 эта формула очень простая:

Утверждение 2 Если

(12)

то

(13)

4.8.2 Максимум и минимум

Производную обычно используют для поиска самого лучшего: Самого большого дохода или самого маленького убытка, или еще чего-нибудь самого большого или самого маленького.

Поразмыслив про Газ, Тормоз, самую большую и самую маленькую скорость, вы, наверное, поймете, что самая большая скорость в тот момент, когда Газ уже отпустили, а Тормоз еще на нажали. А самая маленькая - наоборот. Говоря математически - в тех точках, где производная равна нулю.

Теорема 1 [Ферма] В точках максимума и точках минимума производная равна нулю.

Следует правильно понимать эту теорему:

В ней НЕ сказано, что если производная равна нулю, то в этой точке обязательно максимум или минимум.
В ней сказано, что в точках, где производная НЕ равна нулю, максимума и минимума точно нет, можно не искать.

Как же ею пользоваться?

Найти производную и точки, где она равна нулю. В них максимум и минимум могут быть (а могут и не быть). Это всего лишь подозрительные точки.
Есть в этих точках максимум или минимум, следует проверять дополнительно, другими способами.

4.9 Применение производной

Предположим, вам удалось закончить университет и вы пришли устраиваться на работу. И вам говорят: "Мы решили заняться перепродажей штучек. Сейчас закажем их в интернет магазине, вечером их доставят и утром перепродадим". Оптовая цена у штучки - 50. Потенциальных покупателей у нас 1000. Вопрос: по какой цене продавать. И это действительно вопрос:

Если цену назначить маленькой, то покупателей будет много, но заплатят они мало. Быть может, слишком мало.
Если цену назначить большой, то покупателей будет мало. И заплатят они хоть каждый и много, но в целом мало. Быть может, слишком мало.

Понятно, что требуется найти цену, при которой магазин наварит¹⁴ больше всего.

А еще вам говорят, что провели пробные продажи, но из за недостатка времени их было только две:

На первой пробной продаже из 10 проходящих мимо человек 7 согласились купить штучку за 70 (и 3 отказались).
На второй - из 10 проходящих мимо человек 5 согласились купить штучку за 90 (и 5 отказались).

От вашей попытки решить эту очень жизненную задачу зависит ваше будущее, возьмут вас на работу уборщиком/цей или не уборщиком/цей. Сейчас мы расскажем вам, как решается

4.9.1 Задача про оптимальную цену продажи

Понятно, что спрос (т.е. то, сколько штучек купят покупатели) зависит от цены, чем меньше цена, тем больше спрос. Возникает Функция спроса, т.е. зависимость спроса (количества проданных штучек) от цены.

Понятно, что, вообще говоря, это сложная зависимость, и если рисовать её график, то получится сложная линия. Но мы еще маленькие, и поэтому будем её рисовать в виде прямой линии. А еще мы будем предполагать, что покупать будут по одной штучке в руки (потому что так проще считать).

Поскольку мы можем влиять на цену, то цену обозначим буквой x. Поскольку спрос зависит от цены, обозначим спрос буквой y.

По результатам пробной продажи можно найти две точки на этом самом графике с функцией спроса:

Если цена 70, то купят 7/10 от 1000 покупателей, т.е. 700 человек. Итак, если x=70 то y=700.
Если цена 90, то купят 5/10 от 1000 покупателей, т.е. 500 человек. Итак, если x=90 то y=500.

По двум точкам можно найти уравнение прямой (так, как это сделано в примере 7):

y = −10 ·x + 1400 .

(22)

Это и есть функция спроса, т.е. зависимость спроса (т.е. количества купленных штучек, оно обозначено буквой y) от цены (она обозначена буквой x). С её помощью можно "узнавать будущее":

Пример 64 Если продавать по 100, то покупателей будет −10 ·100 + 1400 = 400 человек. На одной штучке мы наварим (100−50)=50 и всего наварим 400·50=2000.

Упражнение 37 А если продавать по 500? Или по 10? Почему такие странные цифры получаются? Ответ: Наша функция спроса - слишком грубое приближение к реальности. В среднем диапазоне цен оно имеет смысл, при слишком больших или слишком маленьких ценах - не имеет смысла.

Понятно, что навар магазина вычисляется так:

Найдем навар на одной штучке, это цена продажи (это x) минус оптовая цена (это 50). Получится формула (x−50).
Умножим навар на одной штучке на количество проданных штучек (это y). Получится формула y·(x−50).

И, подставив функцию спроса (39) вместо y, найдем формулу зависимости навара от цены:

N = (−10 ·x + 1400)·(x−50)

Осталось найти максимум, как вас учили при подготовке к ЕГЭ.

Упражнение 38 Найдите производную, приравняйте к нулю, найдите максимум, найдите цену, при которой навар самый большой, найдите, сколько штучек купят при такой цене и найдите какой будет навар. Ответ: N′ = (−10)·(x−50) + (−10 ·x + 1400), наилучшая цена - 95, купят 450 штучек (именно столько и надо закупить в оптовом магазине), навар на этой операции будет 20250.