5 июня 15 часов решение. 2 6 Задание на выполнение расчетнографической работы Определение геометрических характеристик поперечного сечения Цель работы
 Скачать 308.19 Kb. Скачать 308.19 Kb.
|
|
2.2.6 Задание на выполнение расчетно-графической работы «Определение геометрических характеристик поперечного сечения» Цель работы: вычисление главных моментов составного поперечного сечения. Для данного сечения требуется:
 Равнобокий уголок  Прямоугольник  Двутавр №30 Решение. Определяем координаты центра тяжести, для чего проводим вспомогательные оси х/ и у/ и разбиваем сечение на три фигуры: прямоугольник (I), двутавр (II) и уголок (III), для которых все необходимые данные находим в таблицах сортамента. Таблица 1 – Исходные данные
  
  где А1 – площадь первой фигуры (прямоугольника); А2 – площадь второй фигуры (двутавра); 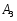 - площадь третьей фигуры (уголка); - площадь третьей фигуры (уголка);х1 – расстояние от оси у/ до центра тяжести прямоугольника; х2 – расстояние от оси у/ до центра тяжести двутавра;  - расстояние от оси у/ до центра тяжести уголка - расстояние от оси у/ до центра тяжести уголкау1 – расстояние от оси х/ до центра тяжести прямоугольника; у2 – расстояние от оси х/ до центра тяжести двутавра.  - расстояние от оси х/ до центра тяжести уголка - расстояние от оси х/ до центра тяжести уголка , ,  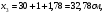      По этим данным наносим точку С – центр тяжести сечения и проводим вертикальную и горизонтальную центральные оси хс и ус. 2) Вычисляем моменты инерции относительно этих осей: 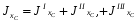 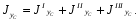 Для вычисления момента инерции прямоугольника 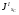 используем формулу используем формулу  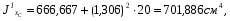 где  – момент инерции прямоугольника относительно собственной центральной оси х1; – момент инерции прямоугольника относительно собственной центральной оси х1; – площадь сечения прямоугольника; – площадь сечения прямоугольника; – координата центра тяжести прямоугольника по оси ус. – координата центра тяжести прямоугольника по оси ус.Для вычисления момента инерции двутавра  используем формулу используем формулу 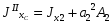 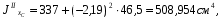 где  – момент инерции двутавра относительно собственной центральной оси х1; – момент инерции двутавра относительно собственной центральной оси х1; – площадь сечения двутавра; – площадь сечения двутавра;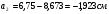 – координата центра тяжести двутавра по оси ус. – координата центра тяжести двутавра по оси ус.Аналогично находим момент инерции уголка  где  – момент инерции уголка относительно собственной центральной оси х2; – момент инерции уголка относительно собственной центральной оси х2;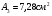 – площадь сечения уголка; – площадь сечения уголка; – координата центра тяжести уголка по оси ус. – координата центра тяжести уголка по оси ус.Суммарный момент инерции сечения относительно оси хс равен 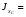  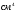 Точно так же вычисляем момент инерции сечения относительно оси ус. Для прямоугольника 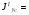  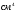 где  – координата центра тяжести прямоугольника по оси хс. – координата центра тяжести прямоугольника по оси хс.Для двутавра 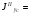  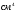 где  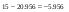 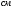 – координата центра тяжести двутавра по оси хс. – координата центра тяжести двутавра по оси хс.Для уголка   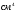 где   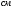 – координата центра тяжести уголка по оси хс. – координата центра тяжести уголка по оси хс.Суммарный момент инерции сечения относительно оси ус равен  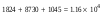 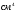 Вычисляем центробежный момент инерции сечения относительно осей хс и ус. Для этого воспользуемся формулой:  (4). (4).  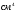
    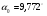 . .Отложим этот угол (против часовой стрелки) и проведем главные центральные оси u и v Вычисляем главные центральные моменты инерции по формуле: 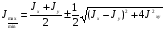  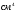 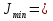 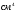 Следовательно,    Рис. 1 Чертеж составного сечения Использованная литература 1.Сорокина О.А. Сопротивление материалов. Классификация усложняющих задач: методические указания. – Кумертау: Кумертауский филиал ГОУ ОГУ, 2010. – 57 с. 2. http://iglin.exponenta.ru/All/SmWeb/MomIner.html#ris1 | |||||||||||||||||||||||||||||||||||
