2. Анализ вычислительной сложности алгоритмов

• Название: 2. Анализ вычислительной сложности алгоритмов
• Анкор: siaod mirea
• Дата: 11.06.2022
• Размер: 74.15 Kb.
• Имя файла: siaod.docx
• Тип: Документы; #584750

Что такое алгоритм:

• 
  Последовательность вычислительных шагов, преобразующих входные величины в выходные *
  

Как называется последовательность вычислительных шагов, преобразующих входные величины в выходные:

• 
  Алгоритмы *
  

Что определяет структура данных:

• 
  Множество данных и отношений между ними *
  

Какие отношения между элементами поддерживает структура данных массив:

• 
  Линейные *
  

Какие существуют уровни уровня представления данных (согласно American National Standards Institute - ANSI):

• 
  Пользовательский, концептуальный, физический *
  

Когда алгоритм считается корректным:

• 
  Когда для каждого ввода результатом его работы является корректный вывод *
  

Какое требование предъявляется к спецификации алгоритма:

• 
  Cпецификация алгоритма должна предоставлять точное описание процедуры, которую требуется выполнить *
  

Как представляются данные в памяти компьютера:

• 
  В виде последовательности битов *
  

Что называют структурой данных:

• 
  Множество элементов данных и внутренних связей между ними *
  

Как называют множество элементов данных и внутренних связей между ними?

• 
  Структура данных *
  

Что такое модель?

• 
  Система, исследование которой служит средством для получения информации о другой системе, представление некоторого реального процесса, устройства или концепции *
  

Тема 2. Анализ вычислительной сложности алгоритмов
Показатели эффективности алгоритмов (или программ) включают:

• 
  Количество выполняемых операций и объем памяти, требуемой для выполнения алгоритма *
  

В чем заключается анализ алгоритма:

• 
  Предсказать требуемые для его выполнения ресурсы *
  

Что измеряется для оценки вычислительной сложности алгоритма:

• 
  Зависимость количества выполняемых основных операций от размера обрабатываемых данных *
  

Когда один алгоритм считается эффективнее другого:

• 
  Если время его работы в наихудшем случае имеет более низкий порядок роста *
  

Временная (вычислительная) сложность алгоритма определяется количеством входных данных. Для простоты входные данные представляются параметром n. Этот параметр пропорционален величине обрабатываемого набора данных и может обозначать:

• 
  Размер массива или файла*
  

Какие основные операции следует учитывать при оценке временной (вычислительной) сложности алгоритмов поиска:

• 
  Операции сравнения *
  

Какие основные операции следует учитывать при оценке временной (вычислительной) сложности алгоритмов сортировки:

• 
  Операции сравнения и перемещения *
  

Какие существуют случаи при выполнении алгоритмов:

• 
  Наилучший, средний и наихудший *
  

Для оценки порядка роста функций, описывающих вычислительную сложность алгоритмов, используются асимптотические обозначения (символики) или нотации. Что обозначает запись f(n)=О(g(n)):

• 
  Множество всех функций, порядок роста которых при достаточно больших n не превышает (меньше или равен) некоторую константу c, умноженную на значение функции g(n) *
  

Для оценки порядка роста функций, описывающих вычислительную сложность алгоритмов, используются асимптотические обозначения (символики) или нотации. Что обозначает запись f(n)=Ω(g(n)) :

• 
  Множество всех функций, порядок роста которых при достаточно больших n не превышает (меньше или равен) некоторую константу c, умноженную на значение функции g(n) *
  

Для оценки порядка роста функций, описывающих вычислительную сложность алгоритмов, используются асимптотические обозначения (символики) или нотации. Что обозначает запись f(n)=ϴ(g(n)) :

• 
  
  
• 
  Множество всех функций, порядок роста которых при достаточно больших n не превышает (меньше или равен) некоторую константу c, умноженную на значение функции g(n) *
  

Укажите правильную аналогию между асимптотическим сравнением двух функций f и g для обозначения f(n)=О(g(n)) и сравнением двух действительных чисел а и b:

• а ≤ b *


Укажите правильную аналогию между асимптотическим сравнением двух функций f и g для обозначения f(n)=Ω(g(n)) и сравнением двух действительных чисел а и b:

• а ≥ b *
Укажите правильную аналогию между асимптотическим сравнением двух функций f и g для обозначения f(n)=ϴ(g(n)) и сравнением двух действительных чисел а и b:

• а = b *
Тема 3. Рекурсивные алгоритмы
Как называется алгоритм, который напрямую или через другие вспомогательные алгоритмы вызывает сам себя:

• 
  Рекурсивный *
  

Какая функция реализует линейную рекурсию:

• 
  Содержит только один вызов самой себя *
  

Что определяет понятие «глубина рекурсии» для рекурсивной функции:

• 
  Наибольшее одновременное количество рекурсивных обращений функции *
  

Какие из приведённых строк кода

intfib(intn)

{

if (n < 2)

return 1;

else { }

}

необходимо записать после else в рекурсивной функции вычисления n-ного числа Фибоначчи:

• 
  return fib (n - 1) + fib (n - 2) *
  

Как определить, что функция реализует каскадную (множественную) рекурсию:

• 
  Вызов функции по любой из всех возможных ветвей алгоритма встречается более одного раза *
  

Что помещается в стек рекурсивных вызовов при вызове рекурсивной функции:

• 
  Адрес точки возврата, значения всех переменных функции текущего вызова *
  

Какова глубина рекурсии следующей функции

intfib(intn)

{

if (n <2) { return 1; }

else { return fib(n - 2) + fib(n - 1); }

}

при вызове fib(5):

• 
  7 *
  

Чем может быть вызвано переполнение стека при выполнении рекурсивной функции с небольшой глубиной рекурсии:

• 
  Неправильно сформулированным условием завершения рекурсии *
  

Рекурсия имеет место, если решение задачи сводится к разделению ее на меньшие подзадачи, выполняемые с помощью одного и того же алгоритма. Когда должен завершиться процесс разбиения задачи на подзадачи:

• 
  Когда достигается простейшее возможное решение *
  

Если время выполнения рекурсивной функции f(n) в наихудшем случае определяется рекуррентным соотношением

Ө(1) при n=1

T(n)={

2T(n/2)+ Ө(n) при n>1

то что является решение этого соотношения:

• 
  O(n log₂n) *
  

Тема 4. Простые алгоритмы сортировки
Что такое инвариант цикла:

• 
  Логическое выражение, истинное после каждого прохода тела цикла и в конце выполнения цикла, зависящее от переменных, изменяющихся в теле цикла *
  

Для чего нужен инвариант цикла:

• 
  Для проверки корректности алгоритма *
  

Если на вход подается последовательность (31,41,59,26,41,58), то какой должен быть вывод алгоритма сортировки:

• 
  (26,31,41,41,58,59) *
  

Как называется алгоритм, который выполнит сортировку исходного массива (3,1,5,2,4) после следующей последовательностью проходов

(1,3,5,2,4), (1,3,5,2,4), (1,3,2,5,4), (1,3,2,4,5),

(1,3,2,4,5), (1,2,3,4,5), (1,2,3,4,5), (1,2,3,4,5)

• 
  Простого обмена *
  

Как называется алгоритм, который выполнит сортировку исходного массива (3,1,5,2,4) после следующей последовательностью проходов

(3,1,4,2,5), (3,1,2,4,5), (2,1,3,4,5), (1,2,3,4,5)

• 
  Простого выбора *
  

Как называется алгоритм, который выполнит сортировку исходного массива (3,1,5,2,4) после следующей последовательностью проходов

(1,3,5,2,4), (1,3,5,2,4), (1,2,3,5,4), (1,2,3,4,5)

• 
  Простой вставки *
  

Что проверяет условие Айверсона в алгоритме сортировки методом простого обмена:

• 
  Наличие обменов о в текущем проходе массива *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки методом простой вставки в наилучшем случае:

• 
  f(n)=О(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки методом простого обмена (с условием Айверсона) в наилучшем случае:

• 
  f(n)=О(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки методом простого выбора в наилучшем случае:

• 
  f(n)=О(n²) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки подсчетом (Counting sort) в среднем и наилучшем случаях:

• 
  f(n)=О(n+k) *
  

Тема 5. Нетривиальные алгоритмы сортировки
Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки шейкерным методом (с условием Айверсона) в наилучшем случае:

• 
  f(n)=О(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки шейкерным методом (с условием Айверсона) в наихудшем случае:

• 
  f(n)=О(n²) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма быстрой сортировки методом Хоара (quicksort) в среднем и наилучшем случаях:

• 
  f(n)=О(n log(n)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма быстрой сортировки методом Шелла в наилучшем случае:

• 
  f(n)=О(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма быстрой сортировки методом Шелла в наилхудшем случае:

• 
  f(n)=О(n²) *
  

Суть алгоритма сортировки методом Шелла заключается в:

• 
  отдельной сортировке элементов, отстоящих друг от друга на расстоянии h, уменьшающеймся на каждом проходе массива до значения 1 *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма быстрой сортировки методом Хоара (quicksort) в наихудшем случае:

• 
  f(n)=О(n²) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма пирамидальной сортировки (Heapsort) в среднем и наихудшем случаях:

• 
  f(n)=ϴ(n log(n)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма турнирной сортировки в среднем и наихудшем случаях:

• 
  f(n)=ϴ(n log(n)) *
  

Алгоритм сортировки подсчетом (counting sort) имеет следующие характеристики эффективности:

• 
  Временная (вычислительная) сложность - f(n)=ϴ(n), дополнительная память - f(k)=ϴ(k) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма сортировки слиянием (Mergesort) в среднем и наихудшем случаях:

• 
  f(n)=ϴ(n log(n)) *
  

Тема 6. Алгоритмы поиска в массивах
Какой зависимостью описывается функция вычислительной сложности алгоритма бинарного (двоичного) поиска в среднем и худшем случаях:

• 
  f(n)=ϴ(log(n)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма интерполяционного поиска в среднем случае:

• 
  f(n)=ϴ(log(log(n)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма интерполяционного поиска в худшем случае:

• 
  f(n)=ϴ(n) *
  

Идея алгоритма интерполяционного поиска основана на:

• 
   выборе новой области поиска по расстоянию между ключом и текущим значением элемента *
  

При построении хеш-таблиц возможно появление коллизий. Коллизия это такая ситуация, когда:

• 
   для разных ключей хэш-функция может принимать одно и тоже значение h(ki) = h(kj) *
  

Идея алгоритма бинарного поиска основана на:

• 
   делении области поиска на две части *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска по бинарному дереву (binary search tree, BST) в лучшем случае:

• 
  f(n)=ϴ(log(n)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска по бинарному дереву в худшем случае (несбалансированное бинарное дерево):

• 
  f(n)=ϴ(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска хешированием в лучшем случае:

• 
  f(n)=ϴ(1) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска хешированием в худшем случае:

• 
  f(n)=ϴ(n) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма линейного (последовательного) поиска в худшем случае:

• 
  f(n)=ϴ(n) *
  

Тема 7. Алгоритмы поиска по образцу
Какой зависимостью описывается функция вычислительной сложности алгоритма прямого поиска в тексте по образцу в худшем случае:

• 
  f(n, m)=ϴ(log(n*m)) *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска в тексте по образцу методом Кнута-Морриса-Пратта в лучшем случае:

• 
  f(n, m)=ϴ(log(n+m)) *
  

В каких случаях алгоритм Кнута-Морриса-Пратта дает подлинный выигрыш по сравнению с другими алгоритмами поиска в тексте по образцу:

• 
  Когда неудачному сравнению образца с текстом предшествовало некоторое число совпадений *
  

В основе алгоритма Кнута-Морриса-Пратта используется:

• 
  Таблица префиксов *
  

В основе алгоритма Бойера-Мура используется:

• 
  Таблица смещений («стоп-символов») *
  

Когда достигается максимальная эффективность алгоритма Бойера-Мура:

• 
  Если образец длинный, а мощность алфавита достаточно велика *
  

Отличительная особенность алгоритма Бойера-Мура:

• 
  Сравнение символов производится начиная с конца образца *
  

Отличительная особенность алгоритма Бойера-Мура:

• 
  После каждого неудачного сравнения производится сдвиг образца вправо в соответствии с таблицей смещений («стоп-символов») *
  

В основе алгоритма Рабина-Карпа используется:

• 
  Хэш-таблица *
  

Какой зависимостью описывается функция вычислительной сложности алгоритма поиска в тексте по образцу методом Бойера-Мура в лучшем случае:

• 
  f(n, m)=ϴ(log(n/m)) *
  

Тема 8. Линейные списки
Какая операция считается недопустимой для линейного односвязного списка:

• 
  Вставка нового элемента перед заданным элементом *
  

Укажите, какими свойствами должна обладать структура данных, предназначенная для хранения среднесуточной температуры воздуха за каждый день месяца, если при ее использовании в программе требуется обращаться и ко всем элементам сразу, и к каждому элементу в отдельности:

• 
  Однородная *
  

Какими свойствами можно характеризовать динамическую структуру данных:

• 
  Размер может изменяться во время работы программы *
  

Какие операции необходимо реализовать при разработке программы управления отдельным элементом структуры данных:

• 
  Добавление нового элемента *
  

Какая структура данных относятся к категории линейных списков:

• 
  Дек *
  

Укажите свойство, характеризующее структуру данных Стек:

• 
  Линейный список с одной вершиной *
  

Имеется описание структуры узла линейного односвязного списка

struct Tnode{ Tdata data; XXXX next;};

Какое определение должно быть на месте XXXX:

• 
  *Tnode *
  

Укажите свойство, характеризующее структуру данных Очередь:

• 
  Удаление элемента возможно с одной из сторон списка *
  

Укажите свойства, характеризующие структуру данных Дек:

• 
  Вставка нового элемента возможна в начало и в конец списка *
  

Какой линейный список подойдет лучше для реализации структуры данных, в которой требуется часто перемещаться как слева направо, так и справа налево:

• 
  Дек *
  

Есть ли ошибка в коде функции f, которая осуществляет получение ссылки на последний узел линейного односвязного списка со структурой узла

struct Tnode{ Tdata data; Tnode* next;};

Tnode *f(Tnode *L)

{

Tnode *q=L;

while(q){ q=q->next; }

return q;

}

• 
  Ошибка в условии while (q) - должно быть while (q->next) *
  

Имеется указатель q на узел в середине линейного однонаправленного списка со структурой узла structTnode{ Tdatadata; Tnode* next;}; Требуется вставить новый узел, ссылку на который хранит указатель qq (узел содержит данные), в позицию, в которой находится узел q. Какую последовательность операторов необходимо выполнить, чтобы корректно выполнилась операция вставки:

• 
  qq->next=q->next; q->next=q; swap(qq->data, q->data); *
  

Имеется линейный однонаправленный список из n (n>1) узлов. Структура узла списка structTnode{ Tdatadata; Tnode* next;}; L - указатель на его вершину. Укажите группу операторов, которые обеспечат корректную вставку в вершину списка L нового узла, адрес которого хранит указатель qq:

• 
  qq->next=L; L=qq; *
  

Имеется линейный однонаправленный список из n (n>2) узлов. Структура узла списка structTnode{ Tdatadata; Tnode* next;}; L- указатель на его вершину. Укажите группу операторов, которые обеспечат корректное удаление двух узлов из вершины списка L:

• 
  q1=L; q2=L->next; L=L->next->next; delete q1;delete q2; *
  

Имеется указатель q на узел в середине линейного однонаправленного списка со структурой узла structTnode{ Tdatadata; Tnode* next;}; Требуется удалить узел, ссылку на который хранит указатель q. Какую последовательность операторов необходимо выполнить, чтобы корректно выполнилась операция удаления узла:

• 
  q1=q->next; *q=*q1; delete q1; *
  

Какой вы выберите способ реализации линейного списка, для задачи, в которой требуется обеспечить наискорейшее выполнение операций вставки и удаления над любым элементом:

• 
  Линейный однонаправленный список *
  

Какой из видов линейных списков лучше использовать при реализации задачи по проверке баланса круглых скобок (соответствие открывающей и закрывающей скобок: (()()) – баланс):

• 
  Стек *
  

Как лучше реализовать линейный связный список, для задачи, в которой часто требуется добавлять узел в конец списка:

• 
  Очередь *
  

Какое минимальное количество операторов потребуется выполнить алгоритму при исключении (не удалении) узла, на который указывает указатель q, из линейного двусвязного списка:

• 
  2 *
  

Какую операцию в линейном двунаправленном списке выполняют следующие операторы q->prev->next=q->next; q->next->prev=q->prev; ? Где q указатель на отдельный узел списка, расположенный в середине списка:

• 
  Удаление узла по указателю q *
  

Какая экономная по памяти структура данных используется для реализации кольцевой (циклической) очереди:

• 
  Массив *
  

Имеется некоторая структура данных, в которую заносятся упорядоченные по возрастанию символы. Считывание данных из этой структуры даёт результат: F, E, D, C, B, A. Чем является эта структура данных:

• 
  Стек *
  

Зачем нужен заглавный элемент в двусвязном кольцевом списке

*для связи последнего и первого
Имеется следующее оптимального кодовое дерево (ОКД). Закодировано 111 0 0 10 10 0 110 0 10 0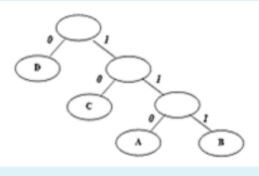


Ответ: BDDCCDFDCD
Какой код будет получен из входной строки символов 11112234444 при использовании алгоритма RLE

*4 1 2 2 1 3 3 4
Какой алгоритм реализует стратегию «разделяй и властвуй»
*quick sort
Как называется алгоритм для нахождения кратчайшего пути меджу двумя вершинами графа

*алгоритм Дейкстры

*О(n^2) (не точно)
Количество ребер в основном дереве равно
*n-1
Сколько байт бинарного файла занимает число 0 в двоичном формате

*1 байт
Что такое структурированный протокол

*Простейший способ записи кластеров данных в файл (не точно)
Известно, что при построении хеш-таблиц возможно появление коллизий. Коллизия это…
*h(ki) = h(kj)
Каков главный недостаток хеш-таблиц

*В статическом распределении памяти
Какое из перечисленных АВЛ-деревьев требует перестройки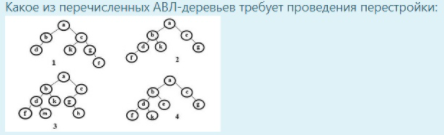



*1 (не точно)
Для каких узлов необходимо проверить коэффициент балансировки после добавления узла в АВЛ-дерево
*для всех предков нового узла вплоть до корня
Имеется идеально сбалансированное двочиное дерево, содержащее 31 узел. Высота

*5 уровней
Имеется идеально сбалансированное двочиное дерево (не явл. деревом поиска). Обход слева-направа in-order: 2 4 6 8 10 12 14.

*2
Какая операция считается недопустимой для линейного односвязного списка:
*вставка нового элемента перед заданным
В основе алгоритма Кнута-Морриса-Пратта используется:
*таблица префиксов