просмотр попытки. Теоретическое описание 3 1 Виды алгоритмов нахождения кратчайшего пути 3 2 Общий принцип алгоритма Беллманафорда 7

• Название: Теоретическое описание 3 1 Виды алгоритмов нахождения кратчайшего пути 3 2 Общий принцип алгоритма Беллманафорда 7
• Анкор: просмотр попытки
• Дата: 23.05.2022
• Размер: 1.11 Mb.
• Имя файла: Kozyrev_KTSO-03-19_kurs_3sem1.docx
• Тип: Задача; #545712

Оглавление

Введение 2

ГЛАВА 1. Теоретическое описание 3

1.1 Виды алгоритмов нахождения кратчайшего пути 3

1.2 Общий принцип алгоритма Беллмана-форда 7

ГЛАВА 2. Описание алгоритмов работы программы 11

2.1 Описание переменных 11

2.2 Описание классов и функций программы 11

2.3 Пример работы программы 14

ГЛАВА 3. Оптимизация кода 16

3.1 Встроенные функции 16

3.2 Целочисленное деление на постоянную 16

3.3 Тестовые замеры 20

Заключение 23

Список литературы 24

Приложение 25

Введение

Задача о реализации алгоритма поиска кратчайшего пути – дано некоторое количество вершинами, между которыми налажено сообщение. Решение этой задачи сводится к нахождению оптимальной длины пути между определёнными вершинами.

При разработке игр нам часто нужно находить пути из одной точки в другую. Мы не просто стремимся найти кратчайшее расстояние, но нам также нужно учесть и длительность движения.



Рис. 1. Схема лабиринта

Для поиска этого пути можно использовать алгоритм поиска по графу, который применим, если карта представляет собой граф. Граф часто используется в качестве алгоритма поиска по графу. Поиск в ширину — это простейший из алгоритмов поиска по графу, поэтому давайте начнём с него и постепенно перейдём к графу.

ГЛАВА 1. Теоретическое описание

1.1 Виды алгоритмов нахождения кратчайшего пути

Алгоритм Дейкстры

Наиболее эффективный алгоритм решения задачи о кратчайшем (s-t)- пути первоначально предложил Дейкстра (1959г.). В общем случае этот метод основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины от s к этой вершине. Эти пометки (их величины) постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является временной, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.

Только что описанный алгоритм Дейкстры применим для нахождения кратчайшего пути между двумя заданными вершинами s и t. Что бы найти кратчайшие пути между всеми парами вершин, можно n-раз воспользоваться алгоритмом Дейкстры, причем каждый раз в качестве начальной вершины s будут браться различные вершины. В этом случае время, необходимое для вычислений, будет пропорционально n3. Поэтому, если задача о нахождении кратчайшего пути имеет большую размерность, то ее невозможно решить с помощью последовательного применения этого алгоритма.

Алгоритм Флойда

Алгоритм Флойда поиска кратчайших путей между всеми парами вершин.

Граф - это совокупность множества вершин и множества пар вершин (связей между вершинами, дуг).

Рассматриваемый алгоритм иногда называют алгоритмом Флойда- Уоршелла. Алгоритм Флойда-Уоршелла является алгоритмом на графах, который разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом. Он служит для нахождения кратчайших путей между всеми парами вершин графа.

Метод Флойда непосредственно основывается на том факте, что в графе с положительными весами ребер всякий неэлементарный (содержащий более 1 ребра) кратчайший путь состоит из других кратчайших путей.

Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя вершинами графа.

В алгоритме Флойда используется матрица A размером nxn, в которой вычисляются длины кратчайших путей. Элемент A[i,j] равен расстоянию от вершины i к вершине j, которое имеет конечное значение, если существует ребро (i,j), и равен бесконечности в противном случае.

Таким образом, алгоритм Флойда делает n итераций, после i -й итерации матрица А будет содержать длины кратчайших путей между любыми двумя парами вершин при условии, что эти пути проходят через вершины от первой до i -й. На каждой итерации перебираются все пары вершин и путь между ними сокращается при помощи i -й вершины.

Разработка блок-схемы алгоритмов

На рисунке 1 представлена разработанная блок-схема алгоритма Флойда, где показано, каким образом, работает этот алгоритм. i, j, k, - аргументы прохода по циклу, N - размер массива расстояний, D[N][N] - массив расстояний.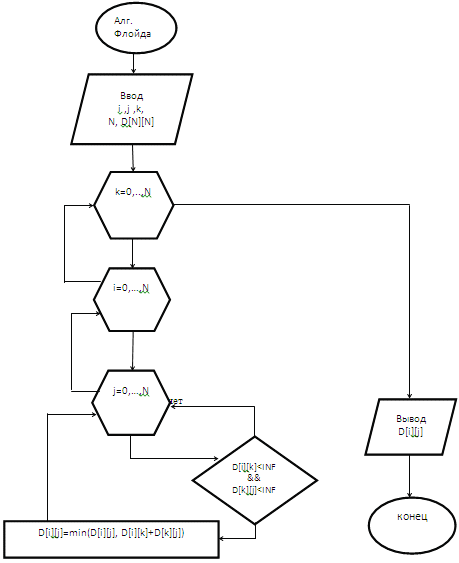



Рис. 2. Блок-схема алгоритма Флойда

На рисунке 2 представлена разработанная блок-схема алгоритма Беллмана-Форда, где показано, каким образом, работает этот алгоритм. Smej - матрица смежности графа, start_v - начальная вершина, mRast - массив существующих в графе дуг, rez - массив кратчайших расстояний, RELAX(rez[mRast[j].to]) - улучшение пути между начальной и j-ой вершиной графа.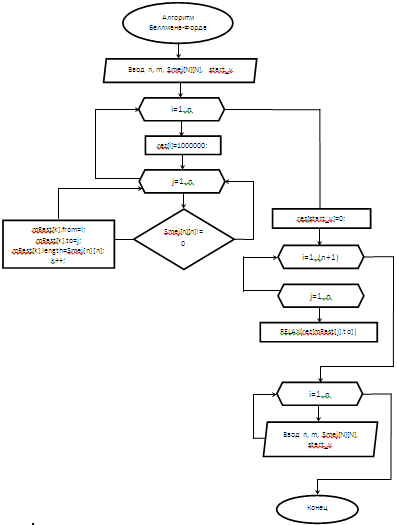



Рис. 3. Блок-схема алгоритма Беллмана-Форда

1.2 Общий принцип алгоритма Беллмана-форда

Формулировка задачи

Дан ориентированный или неориентированный граф G со взвешенными рёбрами. Длиной пути назовём сумму весов рёбер, входящих в этот путь. Требуется найти кратчайшие пути от выделенной вершины до всех вершин графа. Заметим, что кратчайших путей может не существовать. Так, в графе, содержащем цикл с отрицательным суммарным весом, существует сколь угодно короткий путь от одной вершины этого цикла до другой (каждый обход цикла уменьшает длину пути). Цикл, сумма весов рёбер которого отрицательна, называется отрицательным циклом.

Описание

Мы считаем, что граф не содержит цикла отрицательного веса. Случай наличия отрицательного цикла будет рассмотрен ниже в отдельном разделе.

Заведём массив расстояний , который после отработки алгоритма будет содержать ответ на задачу. В начале работы мы заполняем его следующим образом: , а все остальные элементы равны бесконечности Сам алгоритм Форда-Беллмана представляет из себя несколько фаз. На каждой фазе просматриваются все рёбра графа, и алгоритм пытается произвести релаксацию (relax, ослабление) вдоль каждого ребра стоимости . Релаксация вдоль ребра — это попытка улучшить значение значением . Фактически это значит, что мы пытаемся улучшить ответ для вершины, пользуясь ребром и текущим ответом для вершины a.

Утверждается, что достаточно фазы алгоритма, чтобы корректно посчитать длины всех кратчайших путей в графе (повторимся, мы считаем, что циклы отрицательного веса отсутствуют). Для недостижимых вершин расстояние останется равным бесконечности .

Реализация

Для алгоритма Форда-Беллмана, в отличие от многих других графовых алгоритмов, более удобно представлять граф в виде одного списка всех рёбер (а не списков рёбер — рёбер из каждой вершины). В приведённой реализации заводится структура данных для ребра. Входными данными для алгоритма являются числа , список рёбер, и номер стартовой вершины .

Все номера вершин нумеруются с по .

Математическое описание алгоритма

Пусть задан граф G=(V,E) с весами рёбер f(e) и выделенной вершиной-источником u. Обозначим через d(v) кратчайшее расстояние от источника u до вершины v.

Алгоритм Беллмана-Форда ищет функцию d(v) как единственное решение уравнения

d(v)=min{d(w)+f(e)∣e=(w,v)∈E},∀v≠u, с начальным условием d(u)=0.

Свойства алгоритма

Алгоритм может распознавать наличие отрицательных циклов в графе. Ребро e=(v,w) лежит на таком цикле, если вычисленные алгоритмом кратчайшие расстояния d(v) удовлетворяют условию

d(v)+f(e)
где f(e) – вес ребра e. Условие может быть проверено для всех рёбер графа за время O(|E|).

Сравнение алгоритмов по производительности

Алгоритм Беллмана-Форда применяетсяк более широкому классу входных данных, чем алгоритм Дейкстры, потому что может обрабатывать отрицательные веса и обнаруживать отрицательные циклы. Алгоритм Дейкстры не может обрабатывать отрицательные веса ребер, которые обрабатывает Беллман-Форд.  Беллман-Форд выполняет проверку на всех вершинах, Дейкстра только на той, у которой до сих пор было рассчитано лучшее расстояние. Соответственно, алгоритм Дейкстры эффективнее в случае отсутствия отрицательных весов, в то время как алгоритм Беллмана-Форда позволяет нам работать с ними.  Алгоритм Флойда используется, в случае, когда любой узел может быть источником и нам требуется, чтобы кратчайшее расстояние достигло любого конечного узла из любого исходного узла. Алгоритм Флойда работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл.
Таблица 1. Сравнение методов поиска кратчайшего пути

Метод / параметр	Беллман-Форд	Дейкстра	Флойд
Производительность	Средняя скорость; Эффективен только при работе с отрицательными весами и отрицательными циклами	Высокая скорость, ввиду посещения вершины исключительно один раз	Средняя скорость;
Задачи и функционал	Используется, когда одна вершина является источником; Обработка как положительных, так и отрицательных весов; Обнаружение отрицательных циклов; Проверка на всех вершинах;	Используется, когда одна вершина является источником; Обработка только положительных весов; Проверка на одной вершине, у которой было рассчитано лучшее расстояние;	Любой узел может быть источником; Обработка положительных весов, некорректно работает с отрицательными весами; Не может обрабатывать отрицательные циклы;

ГЛАВА 2. Описание алгоритмов работы программы

2.1 Описание переменных

Для реализации алгоритма были задействованы следующие переменные: n – количество вершин, m – количество ребёр, v – номер стартовой вершины, choice2 –переменная для выбора, e – список рёбер, ins – переменная для ввода, os – переменная для вывода, ost – вектор для вывода, Edge eg – ребро для ввода из консоли, Graph G – сам граф, sized – количество ответов.

Код 1. Переменные функций.

int n; int m; int v;

int choice2; vector e; Edge ins; Edge os; vector ost;

Edge eg; Graph G;

int sized;

2.2 Описание классов и функций программы

Информация о ребре, его веса, конечной и начальной вершины используется класс Edge. Для работы алгоритма было принято решение использовать список рёбер для их удобного перебора, где класс vector используется как список рёбер и хранит в себе данные типа Edge. При этом удобность класса vector заключается в том, что он позволяет добавлять элементы в конец вектора. Для хранения информации о рёбрах (откуда (from), куда (to), вес (weight)) задействован класс Edge. В классе также происходит перегрузка операторов ввода/вывода в поток >>, <<.

class Edge

{

public:

int from, to, weight;

Edge(int from = -1, int to = -1, int weight = 0) : from(from), to(to), weight(weight) {}

Edge(const Edge& E)

{

from = E.from; to = E.to;

weight = E.weight;

}

friend ostream& operator<<(ostream& s, Edge& e);

friend istream& operator>>(istream& in, Edge& e);

};

Код 2. Класс Edge.

Для ввода и вывода задействованы операторы ostream – вывод, istream – ввод.

Код 3. Операторы ввода/вывода.

ostream& operator<<(ostream& s, Edge& e)

{

s << "з: " << e.from << ", ': " << e.to << ", 'ес: " << e.weight;

return s;

}

istream& operator>>(istream& in, Edge& e)

{

in >> e.from; in >> e.to;

in >> e.weight;

return in;

}


В классе Graph содержатся метод вывода, (см. в приложении).


13
Для измерения времени исполнения алгоритма задействован класс Timer. Для удобного доступа к вложенным типам используются псевдонимы clock_t и second_t.

class Timer

{

private:

using clock_t = chrono::high_resolution_clock;

using second_t = chrono::duration<double, ratio<1> >; chrono::time_point<clock_t> m_beg;

public:

Timer() : m_beg(clock_t::now())

{

}
void reset()

{

m_beg = clock_t::now();

}

double elapsed() const

{

return chrono::duration_cast(clock_t::now() - m_beg).count();

}

};

Код 5. Класс Timer.

Ввести условия задачи мы можем через командную строку. Интерфейс ввода в данном случае будет выглядеть следующим образом

Рис. 4. Ввод значений через командную строку.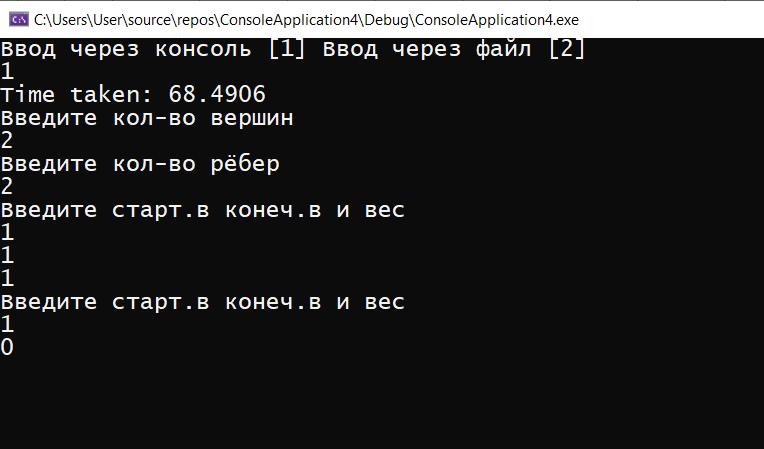

Код 7. Функция ввода из консоли.

void cons()//функция ввода с консоли

{

Edge eg;

cout << "Введите кол-во вершин\n";

cin >> m;

cout << Введите кол-во рёбер\n";

cin >> n;

for (int i = 0; i < m; ++i)

{

cout << "Введите старт.в конеч.в и вес\n";

cin >> eg; e.push_back(eg);

}

cout << «Введите номер стартовой вершины\n";

cin >> v; bellman_ford_v3();

}
Выбор действий в программе реализован на основе конструкции switch- case в функции main.

Код 6. Функция с реализованным меню программы.

int main()

{

setlocale(LC_ALL, "Rus");

int choice;

cout << "Ввод через консоль [1] ввод через файл [2]\n";

cin >> choice;

switch (choice)

{

case 1:

{

cons();

G.bellman_ford(n, m, v, sized, ins, os, e, ost, choice2);

break;

}

case 2:

{

file();

G.bellman_ford(n, m, v, sized, ins, os, e, ost, choice2);

break;

}

default:

{

break;

}

}

}

2.3 Пример работы программы

При запуске программы, нам дается выбор работы. Можно выбрать ввод данных через консоль, либо через файл.



Рис. 5. Запуск программы

При выборе работы через консоль, нам предлагают ввести несколько параметров, такие как количество вершин, количество ребер, вес, стартовую вершину.

Далее, программа определяет наличие отрицательных циклов, а также предлагает нам записать полученный ответ в файл, либо выйти из программы.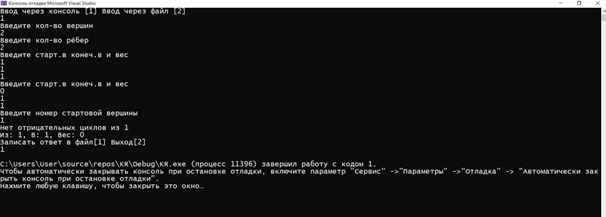



Рис. 6. Полная работа программы

Также при запуске через файл, мы задаем граф (соединение вершин, вес, значение), где 2 – запуск через файл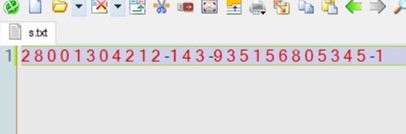


Рис. 7. Запуск через файл

Данные берем из файла s.txt.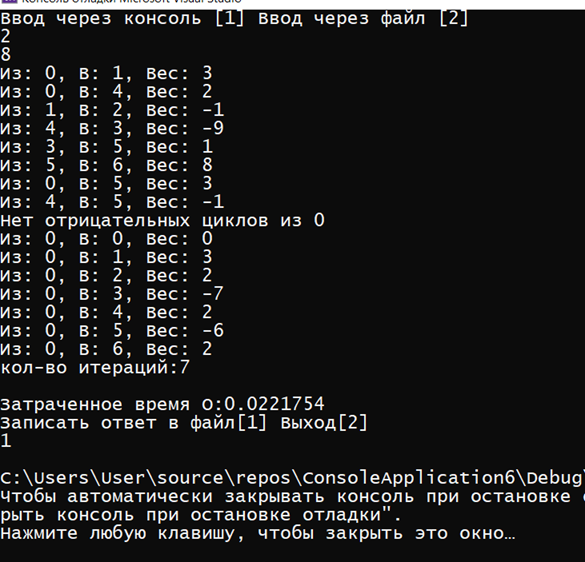



Рис. 8. Работа программы через файл

Ответ выводится в отдельный файл, который сам создается и этот файл называется s2.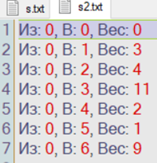




Рис. 9. Результат после обработки данных

ГЛАВА 3. Оптимизация кода

3.1 Встроенные функции

Если вы не используете параметры компилятора для оптимизации всей программы, чтобы компилятор мог встраивать любую функцию, то есть смысл перенести некоторые функции в заголовочные файлы как inline функции, то есть объявить их встроенными.

Если верить руководству (например компилятора gcc "5.34 An Inline Function is As Fast As a Macro"), то inline функция выполняется (так же быстро как макрос) быстрее чем обычная из-за устранения служебных вызовов, но стоит учитывать, что не все функции будут работать быстрее, а некоторые функции, объявленные как inline способны замедлить работу всей программы.

3.2 Целочисленное деление на постоянную

Когда вы делите целое число (которое является положительным или равным нулю) на константу, преобразуйте целое число в unsigned.


16
Например, если s — целое число со знаком, u — целое число без знака, а C — выражение с постоянным целым числом (положительное или отрицательное), операция s / C медленнее, чем u / C, а s% C медленнее, чем u% C. Это проявляется наиболее явно, когда С — степень двойки, но, все же, при делении знак стоит учитываться. Кстати, преобразование из signed в unsigned ничего не будет нам стоить, поскольку это только другая интерпретация одних и тех же битов. Следовательно, если s — целое число со знаком, которое будет использоваться в дальнейшем, как положительное или ноль, вы можете ускорить его деление, используя следующие выражения: (unsigned) s / C и (unsigned) s% C. Для экономии памяти был использован приём выравнивания данных. Выравнивание данных в оперативной памяти компьтеров.

Центральные процессоры в качестве основной единицы при работе с памятью используют машинное слово, размер которого может быть различным. Однако размер слова всегда равен нескольким байтам (байт является наименьшей единицей, в которой отсчитываются адреса).

Как правило, машинное слово равно 2 𝑘 байтам, то есть состоит из одного, двух, четырёх, восьми и т. д. байтов. При сохранении какого-то объекта в памяти может случиться, что некое поле, состоящее из нескольких байтов, пересечёт «естественную границу» слов в памяти. Некоторые модели процессоров не могут обращаться к данным в памяти, нарушающим границы машинных слов. Некоторые могут обращаться к невыровненным данным дольше, нежели к данным, находящимся внутри целого

«машинного слова» в памяти. На практике такое выравнивание означает, что адреса всех данных размером 2 𝑖 байт при 𝑖 ≥ 𝑘 (превосходящие размер слова) должны делиться без остатка на 2.

Код 8. Оптимизация алгоритма Беллмана-Форда с оптимизацией по памяти

unsigned int n; // кол-во р 'бер

unsigned int vert; // кол-во вершин

unsigned int start; // номер стартовой вершины

unsigned int size; // кол-во ответов

unsigned int vibor2;



Необходимо добавить, что удалось добиться оптимизации по времени за счёт сокращения количества итераций до необходимого числа.

Также для экономии памяти все переменные, которые не могут быть отрицательными были заменены на беззнаковые (unsigned). Для ускорения работы программы везде использованы префиксные операторы. Префиксный оператор предпочтительнее постфиксного. При работе с примитивными типами префиксные и постфиксные арифметические операции, вероятно, будут иметь одинаковую производительность. Однако с объектами, операторы постфикса могут заставить объект создать собственную копию, чтобы сохранить свое начальное состояние (которое должно быть возвращено в результате операции), а также вызвать побочный эффект операции. Поскольку операторы постфикса обязаны возвращать неизмененную версию значения, которое увеличивается (или уменьшается) — независимо от того, используется ли результат на самом деле — скорее всего, он сделает копию. Итераторы STL (например) более эффективны при изменении с помощью префиксных операторов. Два ветвления if было заменено на одно с двумя условиями. Для реализации меню приложения использовалось ветвление switch вместо if/else. Реализация алгоритма Беллмана-Форда с небольшой оптимизацией по времени выполнения представлена в приложениях.



Рис. 10. Код до оптимизации.



Рис. 11. Код после оптимизации.

В своей курсовой работе использовал unsigned int, потому что как следует из названий, int - это знаковый целочисленный тип, а unsigned int - беззнаковый целочисленный тип. Это означает, что int может представлять отрицательные значения, а unsigned int может представлять только неотрицательные значения.

Язык C++ накладывает некоторые требования на диапазоны этих типов. Диапазон значений int должен быть не менее -32767 +32767, а диапазон unsigned int должен быть не менее 0,65535 . Это означает, что оба типа должны быть не менее 16 бит. Во многих системах они составляют 32 бита, а в некоторых даже 64 бита. int обычно имеет дополнительное отрицательное значение из-за двухкомпонентного представления, используемого большинством современных систем.

Возможно, самое важное различие - это поведение знаковой и беззнаковой арифметики. Для знака int переполнение имеет неопределенное поведение. Для unsigned int переполнения не существует; любая операция, которая дает значение вне диапазона типа, обтекает его, например UINT_MAX + 1U == 0U. Любой целочисленный тип, как со знаком, так и без знака, моделирует поддиапазон бесконечного множества математических целых чисел. Пока вы работаете со значениями в пределах диапазона типа, все работает. Когда вы приближаетесь к нижней или верхней границе типа, вы сталкиваетесь с разрывом, и вы можете получить неожиданные результаты. Для целочисленных типов со знаком проблемы возникают только для очень больших отрицательных и положительных значений, превышающих INT_MIN и INT_MAX . Для целочисленных типов без знака проблемы возникают при очень больших положительных значениях и при нулевом значении. Это может быть источником ошибок.

Начать оптимизацию стоит с поиска участков кода, которые довольно часто повторяются в процессе работы программы: такие как циклы, подпрограммы или функции. Единичные операнды трогать не стоит, так как это не даст высокого прироста производительности программы. Для оптимизации массивов следует применять следующие методы: использование указателей для сокращения времени работы программы, выравнивание данных для ускорения доступа к данным в оперативной памяти.

Оптимизация обращения к памяти:

• 
  Кэширование. Обращение к кэшу быстрее, так как он ближе к центральному
  
• 
  процессору, чем основная память.
  
• 
  Выравнивание данных. Обращение к переменной эффективнее всего, когда она хранится в памяти по адресу, кратному размеру переменной (размер всегда должен быть степенью двойки).
  
• 
  Динамическое выделение памяти. Имеет скорее больше недостатков, чем преимуществ, так как процесс выделения и освобождения памяти занимает куда больше времени, чем другие типы хранения. Однако такое выделение памяти бывает полезным, когда неразумно ограничивать сверху требуемый объем памяти, а также динамическое выделение памяти позволяет выделять ровно столько памяти, сколько требуется.
  
• 
  Последовательный доступ к данным. Если доступ к данным организовывается последовательно по возрастанию адресов, кэш работает эффективнее.
  

3.3 Тестовые замеры

Произведем тестовые замеры программы после оптимизации.

Рис. 12. Тестовый замер после оптимизации #1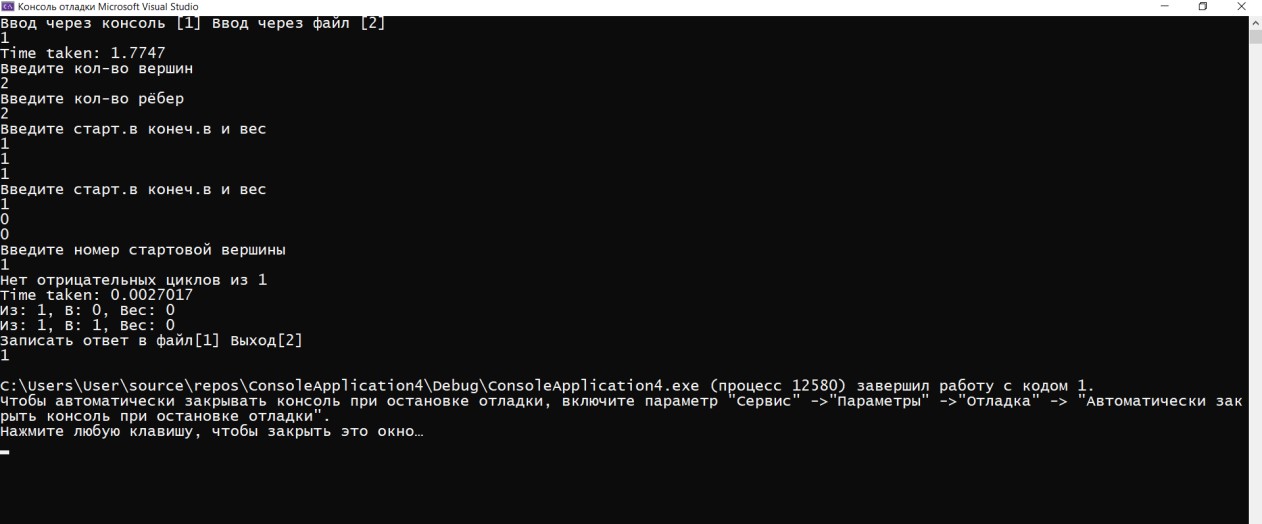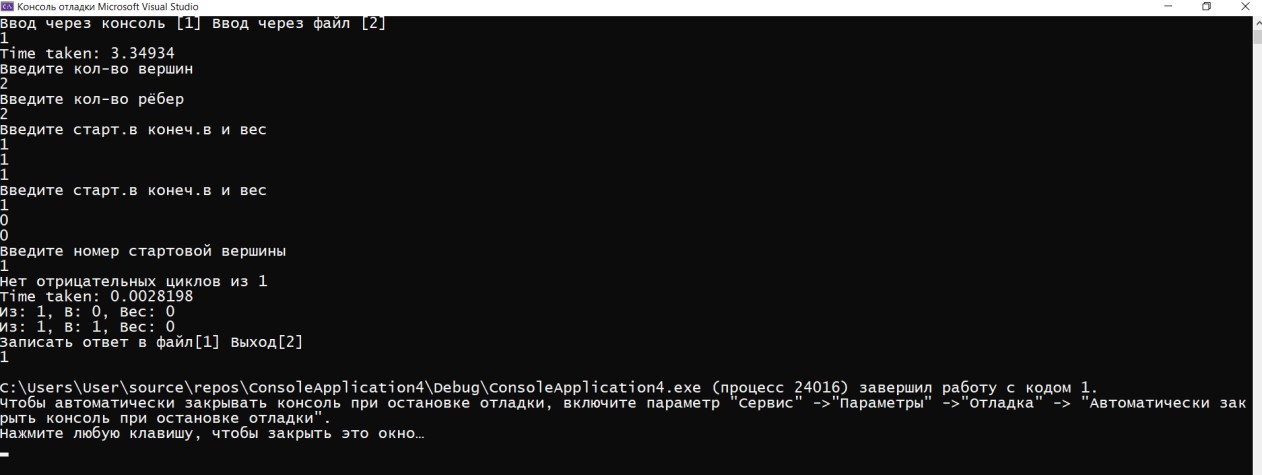

Рис. 13. Тестовый замер после оптимизации #2

Рис. 14. Тестовый замер после оптимизации #3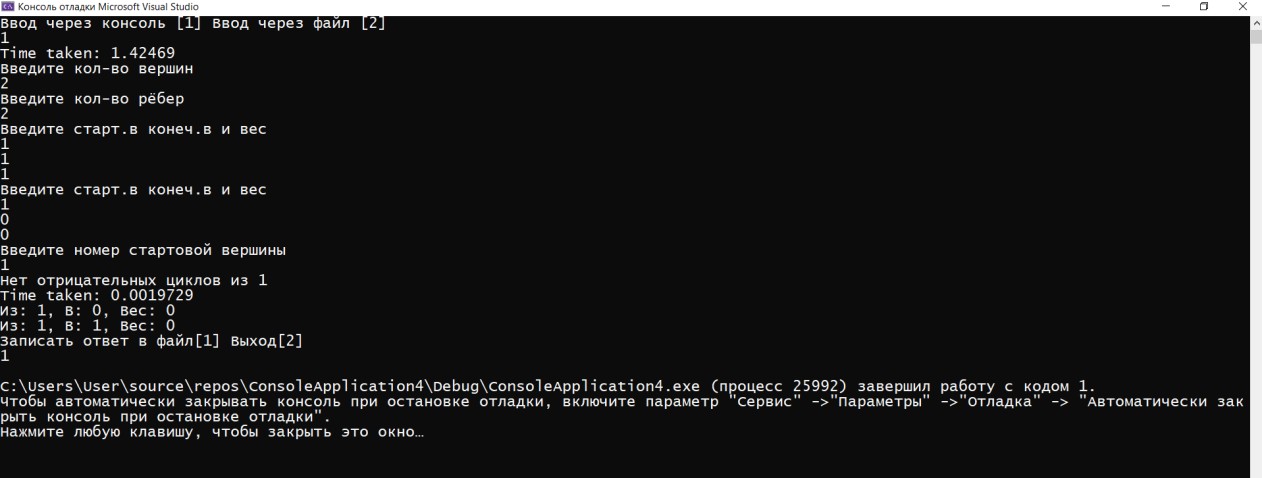

Было произведено 3 тестовых замера для вычисления среднего числа работы: посчитаем среднее значение (0,0019729+0,0028198+0,0027017)/3= 0,0024981333333333

Также, для сравнения, посмотрим на 3 тестовых замера до оптимизации: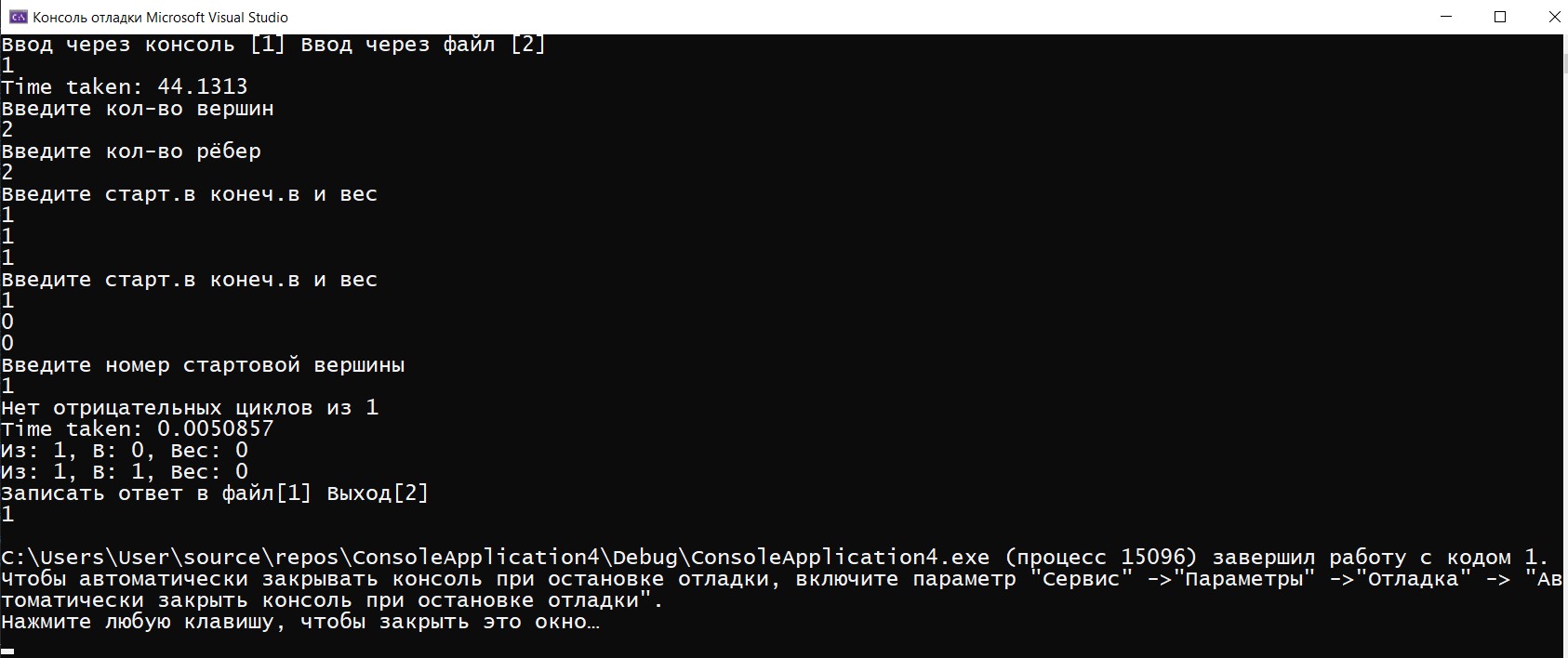



Рис. 15. Тестовый замер до оптимизации #1

Рис. 16. Тестовый замер до оптимизации #2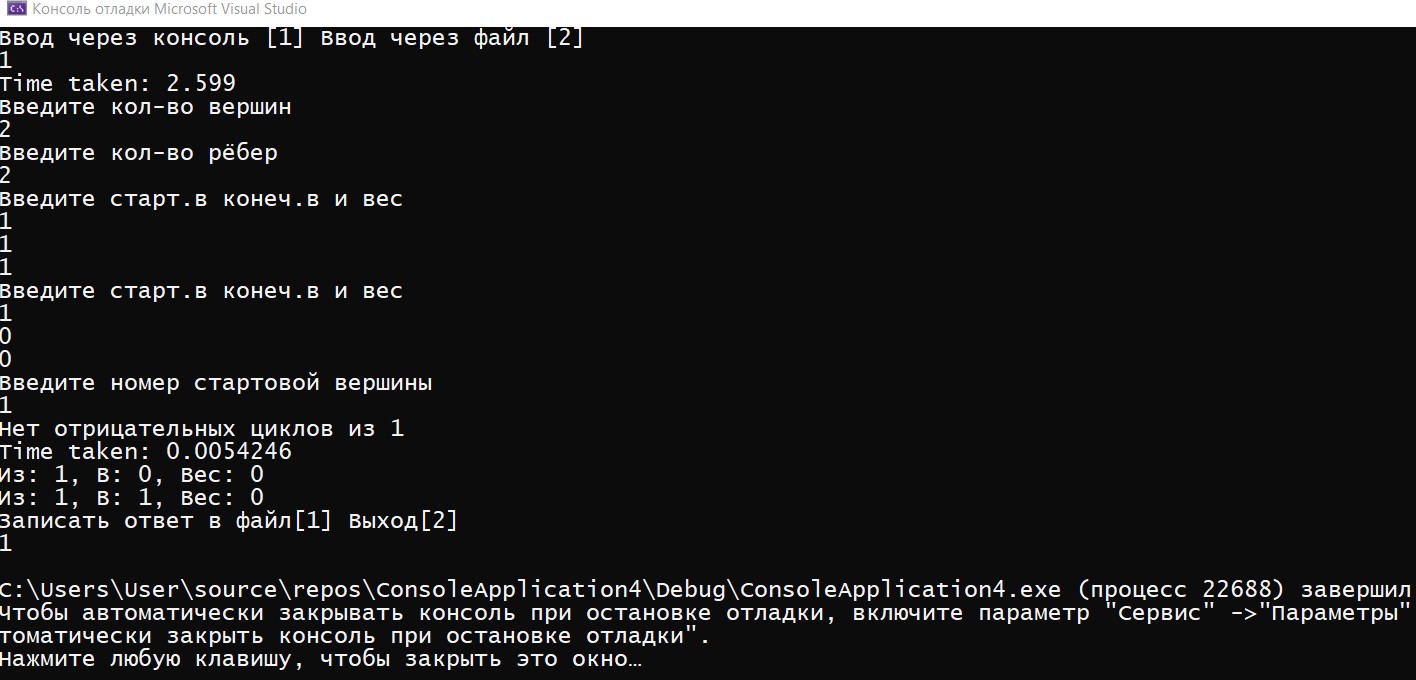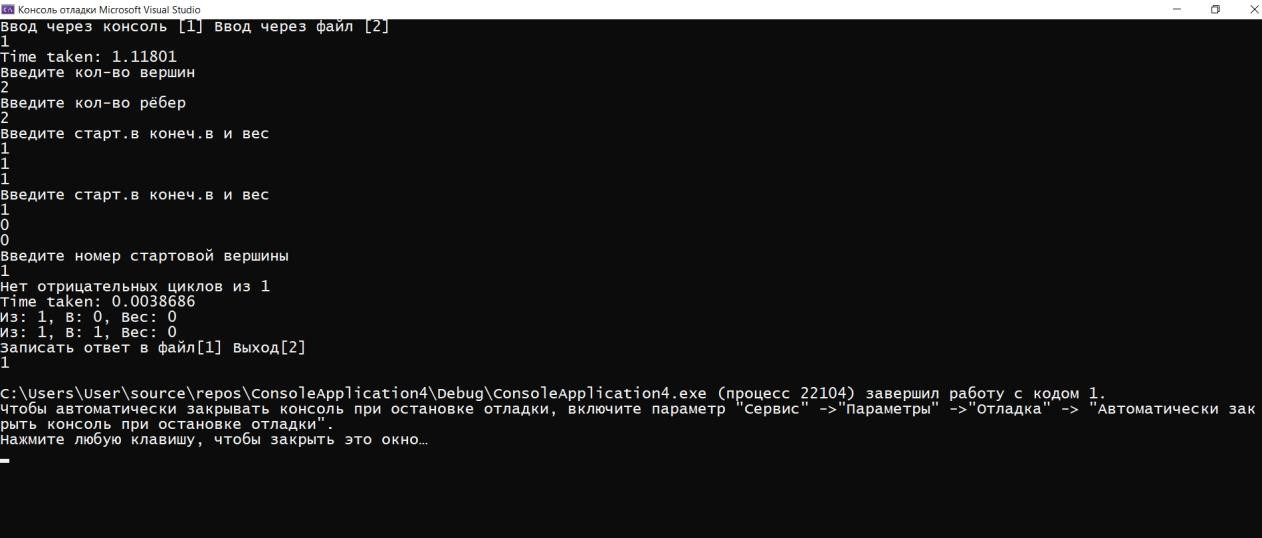

Рис. 17. Тестовый замер до оптимизации #3

Посчитаем среднее значение, без оптимизации

Сред.знач (0,0038686+0,0054246+0,0050857)/3=0,004792966666

Итог: Оптимизированный код работает в 2 раз быстрее!
Заключение

Для достижения поставленной цели потребовалось реализовать алгоритмы Беллмана-Форда в среде (программе) Microsoft Visual Studio. При создании кода программы использовалась программа Microsoft Visual Studio. Получилась программа, позволяющая находить маршрут между двумя пунктами, при этом показывающая отрицательные циклы, а также позволяющая вводить и выводить информацию о графе и из консоли, и из файла. Было проведено сравнение результатов до и после оптимизации кода. Оптимизация позволила сократить время в два раза (0,004792966666 без оптимизации и 0,0024981333333333 после оптимизации). Алгоритм эффективно применяется для задач со взвешенными графами с отрицательными весами, а также позволяет определить наличие отрицательных циклов.

Можно добавить, что поиск пути не тривиальная задача, существует несколько хороших, надежных, и всем известных алгоритмов, которые заслуживают должного внимания в сообществе разработчиков. Помимо представленных выше алгоритмов, хорошо известны такие алгоритмы как алгоритм Дейкстры, алгоритм Флойда, которые используются для разных задач и имеют разные подходы.

Некоторые алгоритмы поиска пути не очень эффективны, но их изучение позволяет постепенно вводить концепции. Так можно понять, как решаются различные проблемы.
Список литературы

1. 
   Гербер Р. Оптимизация ПО / Р. Гербер, А. Бик, К. Смит, К. Тиан; Москва: издательство «Вильямс», 2010. - 262 с.
   
2. 
   Кормен Т. Алгоритмы: Построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест; Москва: издательство «Вильямс», 2011. - 316 с.
   
3. 
   Шилдт Г. Искусство программирования на С++ / Г. Шилдт; Москва: издательство «ПРИОР», 2005. - 102 с.
   
4. 
   Климова Л.М. Основы практического программирования на языке Си++ / Л.М. Климова; Москва: издательство «ПРИОР», 1999. - 464с.
   
5. 
   Пахомов Б. И. C/C++ и MS Visual C++ 2012 для начинающих / Б. А. Пахомов; СПб: издательство «БХВ-Петербург»,2015. - 518 с.
   
6. 
   Топп У. Структуры данных в Си++ / У. Топп, У. Форд; Москва: издательство «Вильямс», 1999. - 800 с.
   
7. 
   Смирнов А.В. Моделирование и анализ информационных систем / А. В. Смирнов; Москва: издательство «Вильямс», 2017. - 788-801 с.
   
8. 
   Макконелл Д. Основы современных алгоритмов / Д. Макконелл; издательство «Техносфера», 2004. - 368 с.
   

Приложение