2 дріс Минор жне алгебралы толытауыш. Лаплас теоремасы
 Скачать 32.5 Kb. Скачать 32.5 Kb.
|
|
№ 2 дәріс Минор және алгебралық толықтауыш. Лаплас теоремасы. Анықтауыштың элементiнiң миноры және алгебралық толықтауышы ұғымдарын қарастырайық. Егер анықтауыштың i-жатық жолымен j-тiк жолын сызып тастап, қалған элементтердiң орынын ауыстырмай олардан ретi бiрге кем анықтауыш құрсақ, оны осы анықтауыштың 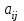 элементiнiң миноры деп атаймыз. элементiнiң миноры деп атаймыз.Мысал.  ; ; 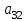 элементiнiң миноры мына анықтауыш элементiнiң миноры мына анықтауыш 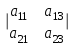 болады. Минор былай белгiленедi болады. Минор былай белгiленедi 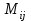 . Ал (-1)i+j таңбасымен алынған минор, яғни . Ал (-1)i+j таңбасымен алынған минор, яғни 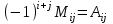 – анықтауыштың – анықтауыштың 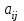 элементiнiң алгебралық толықтауышы деп аталады. элементiнiң алгебралық толықтауышы деп аталады.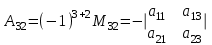 ; ; Мына теорема орындалады. Лаплас теоремасы. Анықтауыштың кез келген бiр жатық (немесе тiк) жолының элементтерiнiң алгебралық толықтырмасын осы элементке көбейтiп олардың қосындысын тапсақ, онда анықтауыштың мәнi шығады. Яғни,  Теореманың орындалуын үшiншi реттi анықтауышта көрсетейiк 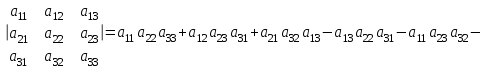 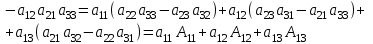 Теореманы жоғары реттi анықтауыштарды есептеуге қолданамыз.  . Болатынын дәлелдеусiз келтiрейiк. . Болатынын дәлелдеусiз келтiрейiк.Мысал.  ;Үшiншi жатық жол элементтерi арқылы анықтауышты жiктеймiз. ;Үшiншi жатық жол элементтерi арқылы анықтауышты жiктеймiз.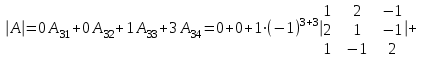 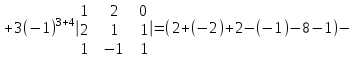 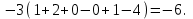 Ескерту. Анықтауышты есептеу үшiн нөлдерi көп жолды алу керек. |
