Курсовая гидравлика. 1 вариант изб прав. 2 Гидравлический расчет разветвленного трубопровода
 Скачать 231.63 Kb. Скачать 231.63 Kb.
|
|
2 Гидравлический расчет разветвленного трубопровода Резервуары 1,2,3 соединены трубами, как показано на рисунке 2. По ним течет нефть (вязкость ν, плотность ρ). Третья труба имеет открытую задвижку. Трубы стальные сварные, с большими отложениями. На поверхности жидкости в резервуаре 1 создано избыточное давление PМН. Определить расходы в трубах и напор в точке С. 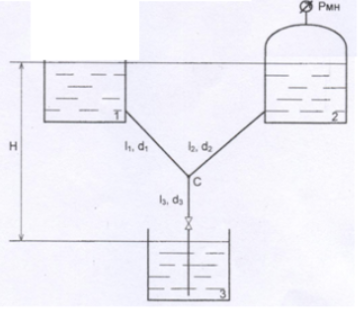 Рисунок 2 – Схема разветвленного трубопровода Исходные данные:
Эквивалентная шероховатость_Кэ= 1 мм___________ 3.1. Теоретическая часть Для решения сформулированных выше задач составляется система уравнений, устанавливающая связи между размерами труб, расходами жидкости, напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравнений Бернулли для каждой ветви трубопровода. При этом в сложных трубопроводах можно пренебрегать относительно малыми местными потерями напора в узлах. Это позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и оперировать в уравнениях Бернулли понятием напора в данном узле. Уравнение Бернулли для участка трубопровода 1-2 записывается в виде 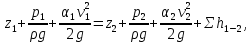 (1) (1)где z – геометрический напор; 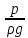 - пьезометрический напор; - пьезометрический напор;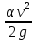 - скоростной напор; - скоростной напор;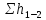 - потери напора; - потери напора;В данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому Потери напора в трубах выражаются формулой Дарси–Вейсбаха (см.[2] стр. 103): 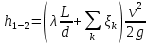 , (2) , (2)где L - длина трубы; d - диаметр трубы; λ - коэффициент сопротивления трения; ξ - коэффициент местного сопротивления; υ - средняя скорость потока в трубе. Поскольку средняя скорость потока в трубе выражается формулой 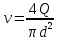 , (3) , (3)где Q - расход жидкости в трубе; то потери напора можно написать в следующем виде 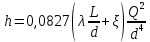 . (4) . (4)Коэффициент гидравлического сопротивления λ зависит от режима течения жидкости и является функцией расхода Q . Так, если режим течения ламинарный ( 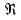 < < 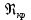 = 2300 и, с учётом того, что = 2300 и, с учётом того, что 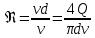 , условие перепишется так , условие перепишется так 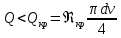 . .Запишем эмпирические формулы для определения коэффициента гидравлического сопротивления λ для каждого режима Таблица 1 – Зависимости коэффициента гидравлического от режима течения.
где 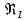 , , 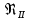 – переходные числа Рейнольдса, определяемые как: – переходные числа Рейнольдса, определяемые как: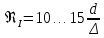 , (5) , (5)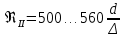 . (6) . (6)3.2. Расчётная часть Данную схему можно разбить на 3 простых трубопровода, причем резервуар 1 (l1,d1) всегда является питающим, резервуар 3 (l3,d3) всегда является приемным, а резервуар 2 (l2,d2) может быть как питающим, так и приемным. 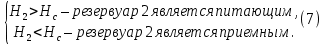 Таким образом, задача сводится к определению направления жидкости в трубопроводе 1. Для определения направления жидкости в трубопроводе 2 пользуются методом отсечения. То есть трубопровод 1 считается как будто перекрытым. Составим уравнения Бернулли для трубопроводов 2 и 3 относительно плоскости отсчета. При этом начальное сечение трубопровода 2 соответствует уровню H, а конечное сечение – в т. С; начальное сечение трубопровода 3 соответствует т. С, а конечное сечение – свободной поверхности в резервуаре 3. Чтобы определить тип резервуара 1, отключим его и вычислим статический напор. Составим систему уравнений Бернулли для трубопроводов 1-C и С-3 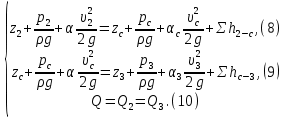 Пренебрегая скоростными напорами и обозначая 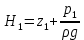 , , 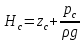 , , 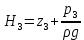 , преобразуем систему , преобразуем систему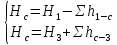 1) Вычислим 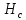 при Q = 5 м3/ч для трубопровода 2-C. при Q = 5 м3/ч для трубопровода 2-C.Рассчитаем 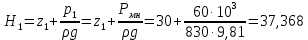 м. м.Найдем среднюю скорость потока 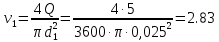 м/с. м/с.Число Рейнольдса 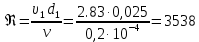 Определим граничные числа Рейнольдса 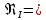 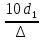 , , 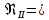 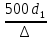 , ,Трубы стальные сварные с большими отложениями примем  мм. мм.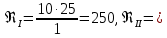 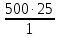 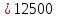 ; ;Т.к. ReI < 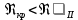 , режим – турбулентный, зона смешанного трения и коэффициент гидравлического трения λ определяется по формуле Альтшуя: , режим – турбулентный, зона смешанного трения и коэффициент гидравлического трения λ определяется по формуле Альтшуя: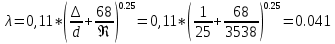 ; ;Вычислим полные потери напора, учитывая коэффициент местных сопротивлений 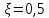 (вход в трубу) (вход в трубу)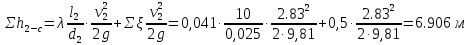 . .Расчитаем статический напор 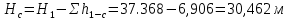 . .Аналогично рассчитаем 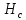 для других значений расхода, данные занесем в таблицу 2. для других значений расхода, данные занесем в таблицу 2.Таблица 2 – Расчетные данные для трубопровода 2
Аналогично для участка С-3 рассчитаем 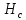 , принимая диаметр и длину соответствующей трубы и коэффициенты местных сопротивлений для задвижки - , принимая диаметр и длину соответствующей трубы и коэффициенты местных сопротивлений для задвижки - 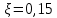 , для тройника - , для тройника - 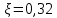 , для внезапного расширения (выход из трубы) - , для внезапного расширения (выход из трубы) - 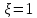 . Рассчетные данные занесем в таблицу 3. . Рассчетные данные занесем в таблицу 3.Таблица 3 – Расчетные данные для трубопровода 3
Построим совмещенную характеристику трубопровода 1 и 3 (рисунок 3). Найдем точку пересечения и ее координату напора H, который будет соответствовать напору в т. С. 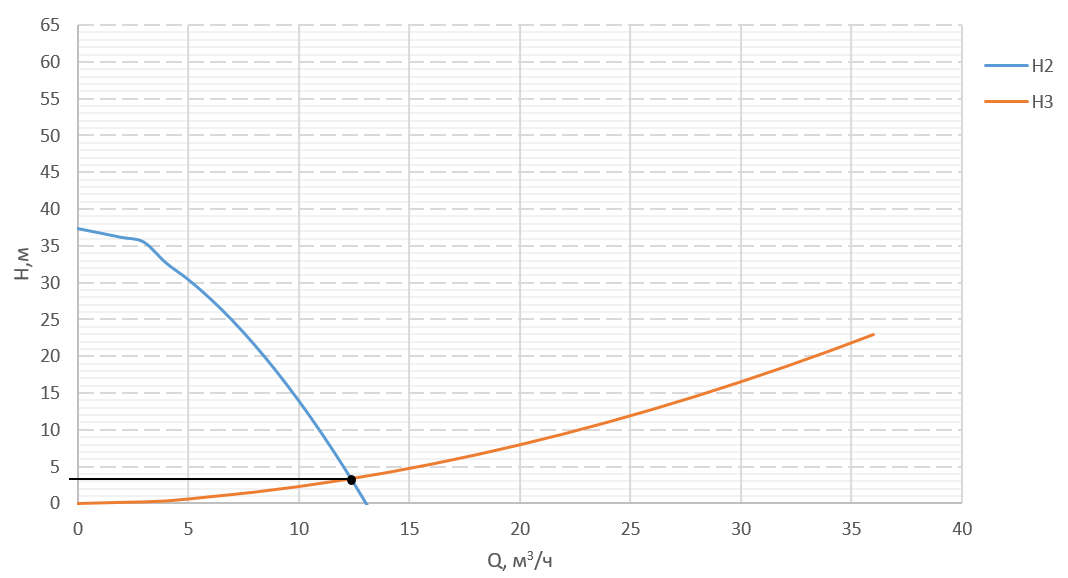 Рисунок 3 – совмещенная характеристика 2 и 3 трубопровода. Полученное значение напора Hcсравнис с напором H1. 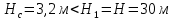 . .Значит резервуар 1 является питающим. Запишем уравнение Бернулли для участка 1-С 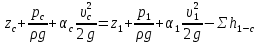 , ,пренебрегая скоростными напорами, получим 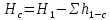 . .Запишем систему уравнений для всего трубопровода 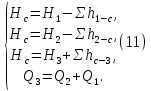 Аналогично для участка C-2 рассчитаем Hc, принимая диаметр и длину соответствующей трубы, а коэффициент местного сопротивления для внезапного сужения (вход в трубу) - 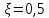 , данные занесем в таблицу 4. , данные занесем в таблицу 4.Таблица 4 – Расчетные данные для трубопровода 1
Далее решаем полученную выше систему уравнений графоаналитически (рисунок 4). Построим график системы уравнений (11) в координатах Н-Q. Далее сложим графически кривые трубопровода 1 и 2 путем добавления расхода в трубопроводе 1 к расходу в трубопроводе 2 при одинаковом значении напора. Полученная «оранжевая» кривая представляет собой эквивалентную гидравлическую характеристику.      Q1 Q2 Q3 Q, м3/с Н,м 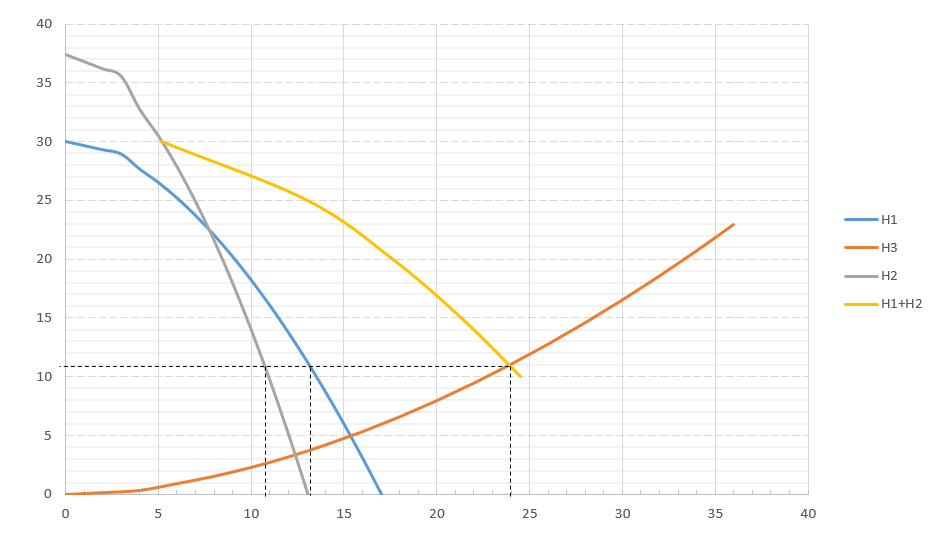 Рисунок 4 – Совмещенная характеристика трубопроводов 1,2 и 3 и суммарной характеристики 1 и 2 трубопровода. По графику находим значения расходов 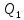 , ,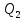 , ,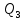 : :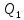 = 13,2 = 13,2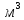 /ч /ч 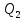 = 10,7 = 10,7 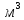 /ч /ч 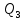 = 23,9 = 23,9 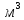 /ч /ч 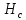 = 10,8 м. = 10,8 м.СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1 Гидромеханика: учеб. пособие по решению задач / Л. Н. Раинкина - М.: Нефть и газ РГУ нефти и газа им. И.М. Губкина, 2005. - 131 с. 2 Прикладные задачи гидравлики: учебное пособие по дисциплинам «Гидравлика» и «Гидромеханика» / Е.Г. Разбегина, А.Р. Сумбатова. – М.: РГУ нефти и газа им.И.М.Губкина, 2007. – 86 с. 3 Учебно-методическое пособие к выполнению курсовой работы по дисциплине «Гидравлика и нефтегазовая гидромеханика» / сост. Л.Р. Байкова, Э.С. Бахтегареева, А.А. Гудникова. – Уфа.: Изд-во УГНТУ, 2014. – 29. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

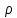 ,
,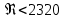
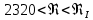
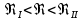
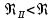
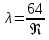
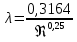
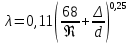
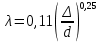
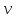 , м/с
, м/с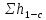 , м
, м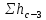 , м
, м