Задача 2. 2. гидравлический расчет внутрипромыслового нефтепровода
 Скачать 77.07 Kb.
|
2. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ВНУТРИПРОМЫСЛОВОГО НЕФТЕПРОВОДАТрубопроводы системы сбора и подготовки нефти предназначены для транспортировки продукции скважин от их устья до сдачи ее товарно-транспортным организациям, а также для перемещения ее в технологических установках, а трубопроводы системы поддержания пластового давления - для подачи сточных вод от установок подготовки воды до нагнетательных скважин. Особые требования предъявляются к строительству трубопроводов газовых и газоконденсатных промыслов. Это связано с обстоятельствами, вызывающими коррозию трубопровода: газ транспортируется под большим давлением и с большей скоростью; газ зачастую содержит больше сероводорода и углекислого газа, чем нефть. Основные уравнения гидравлических расчетовтрубопроводов За основу гидравлических расчетов трубопроводов принимается уравнение Бернулли: ℎпп = (𝑧1 + 𝑝1 𝜌g 𝑣2 1 1 - 2 + 𝛼 ) (𝑧 + 2g 𝑝2  𝜌g 𝑣2 2 2 (2) + 𝛼 ) 2g где 𝑧 - определяет высоту положения различных точек линии тока над плоскостью сравнения, геометрический напор, удельная потенциальная энергия положения; 𝑝 𝜌g называется пьезометрический напор или статический напор, удельная потенциальная энергия давления; 𝑣2 - называется динамический или скоростной напор, или 2g удельная кинетическая энергия; 𝛼 - коэффициент Кориолиса. Объемный расход жидкости определяется из формулы: 𝑄 = 𝑣 · 𝑆, (2.1) где 𝑣 средняя скорость потока жидкости, м/с; 𝑆 площадь поперечного сечения потока, м2. Массовый расход жидкости находят по формуле: 𝐺 = 𝑄 · 𝜌 = 𝑣 · 𝑆 · 𝜌 , (2.2) где 𝜌 плотность жидкости, кг/м3. Для трубопровода, имеющего сечение круглой формы, формула (2.1) примет вид: 𝑄 = 𝜋 · 𝑑2 4  · 𝑣 = 0,785 · 𝑑2 · 𝑣, (2.3)где 𝑑 внутренний диаметр трубопровода, м. В уравнении материального баланса потока объемный расход жидкости определяется как: 𝑄 = 𝑆1 · 𝑣1 = 𝑆2 · 𝑣2 = 𝑐𝑜𝑛𝑠𝑡. (2.4) Массовый расход жидкости: 𝑄 = 𝑆1 · 𝑣1 · 𝜌1 = 𝑆2 · 𝑣2 · 𝜌2 = 𝑐𝑜𝑛𝑠𝑡, (2.5) где 𝜌1 и 𝜌2 плотности жидкости в сечениях 𝑆1 и 𝑆2 соответственно, кг/м3. Гидравлическиесопротивления В случае изотермического течения потока потеря давления на преодоление сил трения в прямой трубе при любом режиме течения определяется по уравнению Дарси-Вейсбаха: или 𝑙 · 𝑣2  ℎ𝑛 = 𝜆 𝑑 · 2𝑔 (2.6)2 𝑃 = 𝜆 𝑙 · 𝜌 · 𝑣2  2𝑑 , (2.7) После подстановки в уравнение (2.6) значения скорости согласно формуле (2.3) получим: 𝑙 · 16𝑄2  ℎ𝑛 = 𝜆 𝑑 · 2𝑔 · 𝜋2𝑑4 . (2.8)Потребный напор (или перепад давления) в наклонном трубопроводе определяется как: или 𝑙 · 𝑣2 ∆ℎ𝑛 = 𝜆 𝑑 · 2𝑔 ± ∆𝑍 (2.9)𝑙 · 𝜌 · 𝑣2 ∆𝑃 = 𝑃 𝑃 = 𝜆 ± ∆𝑍𝜌𝑔 , (2.10) 2𝑑где ∆𝑍 – разность геодезических отметок (альтитуд) трубопровода, м; 𝑔 ускорение свободного падения, м/с2; 𝑙 длина трубопровода, м. 𝜆 – коэффициент гидравлического сопротивления, зависящий от режима движения жидкости и от относительной шероховатости внутренней стенки трубы). Коэффициент гидравлического сопротивления находится как: 𝜆 = ƒ(𝑅𝑒, s),  s = 2𝑒.𝑑 где e – абсолютная шероховатость стенок трубы, м (средняя высота выступов неровностей, измеренная в линейных единицах) d – внутренний диаметр трубы, м. Режим движения жидкости в трубопроводе характеризуется числом Re, являющимся мерой отношения сил инерции к силам внутреннего трения и определяемым по формуле: 3 𝑅𝑒 = 𝑣𝑑  =4𝑄  =𝜋𝑑 4𝑄𝜌  𝜋𝑑𝜇 (2.11) где 𝑣 – средняя скорость потока, м/с; 𝜌 – плотность жидкости, кг/м3; 𝜇, – соответственно динамический и кинематический коэффициенты вязкости, Па·с и м2/с;  Если течение жидкости в трубе ламинарное (струйное), т.е. когда Re < 2320, то, по Стоксу, 𝜆 = 64 , и не зависит от𝑅𝑒 шероховатости стенок трубы. При турбулентном течении жидкости, когда Re > 2320, для определения 𝜆 имеется целый ряд экспериментальных формул. Область турбулентного течения жидкости подразделяется на три зоны: Гидравлически гладких труб, когда потери на трение, а, следовательно, и коэффициент гидравлического сопротивления не зависят от внутренней шероховатости трубы; Переходную зону (смешанного трения), когда 𝜆 зависит от режима течения жидкости Re и шероховатости ε; Гидравлически шероховатых труб (квадратичного трения), когда 𝜆 зависит только от шероховатости трубы и не зависит от режима течения жидкости. Эта зона также называется автомодельной зоной. Эти три зоны разделяются между собой так называемыми переходными числами Рейнольдса, которые найдены на основании экспериментальных данных, и характеризуются следующими величинами: гидравлически гладкие трубы 2320 < Re < Reпер1 переходная зона Reпер1 < Re < Reпер2 квадратичное течение жидкости Re > Reпер2 Числа Рейнольдса в переходных зонах определяют по следующим формулам: 𝑅𝑒 п 1 = 59,5, 𝑅𝑒  𝗌 п 2 = 665−765·𝑙g𝗌  𝗌Для зоны гидравлически гладких труб при Re ≤ 105 коэффициент гидравлического сопротивления λ определяют по 4 формуле Блазиуса: 𝜆 = 0,3164  4 (2.12)√𝑅𝑒 Для определения коэффициент гидравлического сопротивления в зоне смешанного трения применяют «универсальные» формулы, суть которых сводится к тому, что при малых Re они обращаются в формулы типа λ = f(𝑅𝑒), а при больших – переходят в формулы λ = f(s). Наибольшее распространение получили следующие методики: Формула Исаева: 1  𝗌 1,11 + 6, , = −1,8 · lg(( ) √ 3,7 ) 𝑅𝑒 Формула Альтшуля: 𝜆 = 0,11 · (s + 6 𝑅𝑒 ,25 ) ,  Формула Колбрука-Уайта: 1√ = −2 · lg( 𝗌 3,7+ 2,51 ).  𝑅𝑒√ ( - эквивалентная шероховатость) Формула Никурадзе (для квадратичного трения): 1  𝜆 = (1,74 − 2 · 𝑙𝑔s)2Местныесопротивления Местными сопротивлениями называются участки трубопровода, в которых происходит резкая деформация потока (к ним относятся, в частности, все виды арматуры трубопроводов – вентили, задвижки, тройники, колена и т.д.). Потери напора в местных сопротивлениях hм.с. определяются по формуле Вейсбаха (в долях скоростного напора). ℎm.c. = Ç 𝑣2 2g(3.13) где v- средняя скорость потока за местным сопротивлением; ζ- коэффициент местного сопротивления, зависящий от его геометрической формы, состояния внутренней поверхности и Re, а для запорных устройств - от степени их открытия. Величины местных сопротивлений можно найти в литературе. 5 ЗаданиеЗадача 2.1 Определить необходимый перепад давления и диаметр трубопровода для перекачки нефти. Исходные данные приведены в табл. 2.1., дополнительные – в табл. 2.2 и 2.3. Значения коэффициентов местных сопротивлений брать согласно рис. 2.1. Указаниекрешениюзадачи. При расчете диаметра трубопровода и необходимого перепада давления ориентируются на регламентированные скорости нефти (табл. 2.2). Диаметр трубопровода определяется исходя из формулы (2.3). По ГОСТу (таблица 2.3) подбирается труба, соответствующая этому размеру. В расчетах получается внутренний диаметр, а в ГОСТе указывается наружный. Поэтому наружный диаметр D определяется с учетом толщины стенки трубы δ. По табл. 2.3 выбирается ближайший в большую сторону диаметр трубы. По фактическому внутреннему диаметру dвыбранной трубы рассчитывается фактическая скорость потока, параметр Рейнольдса Reи коэффициент гидравлического сопротивления . Далее определяется необходимый перепад давления с учетом гидравлических сопротивлений и геометрии трубопровода. Таблица 2.1 Исходные данные для расчета
6
7
Таблица 2.2 Рекомендуемая скорость нефти в зависимости от вязкости
Таблица 2.3 Трубы стальные бесшовные горячекатаные (ГОСТ 8732-70)
8 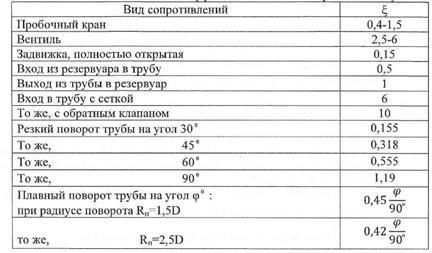 Рисунок 2.1 – Значения коэффициентов местных сопротивлений Задача 2.2На дожимной насосной станции в сепараторе первой ступени поддерживают давление 0,6 МПа. Длина сборного коллектора, идущего от АГЗУ до ДНС, l, а внутренний диаметр его d. Сборный коллектор горизонтален. Массовый расход перекачиваемой нефти G, ее плотность ρ, кинематическая вязкость ν. Определить необходимое начальное давление. 9 |