Билеты по ГА. Билеты по гидре хз хз хз. 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта
 Скачать 0.8 Mb.
|
|
Модель Ньютона.  , (В.1) касательное напряжение в жидкости при слоистом, упорядоченном течении прямо пропорционально градиенту скорости. Коэффициент пропорциональности μ принимается за меру вязкости и характеризует это свойство жидкости.Уравнение (В.1) – это математическое выражение ньютоновской модели жидкости. Из формулы следует, что μ – это сила трения, приходящаяся на единицу поверхности трения, при градиенте скорости равном единице. Для того чтобы жидкость полностью подчинялась ньютоновской модели, необходимо, чтобы величина μ не зависела от градиента скорости du/dy. Это, в частности, означает, что с увеличением скорости жидкость и не разжижается, и не становится более вязкой. Зависимость 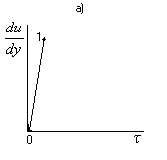 в таких случаях графически изображается в виде прямой, исходящей из начала координат. Экспериментально полученный график зависимости  называется реологической кривой или реограммой.  . На рис. В.1 показаны типичные реограммы реологически стационарных систем. Прямая 1 на рис. В.1а – это типичная зависимость между τ и градиентом скорости du/dy, соответствующая модели Ньютона (В.1). 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта. Введем допущения: - газ не растворяется в жидкости; - процесс всплытия происходит в изотермических условиях; - скважина герметична. Зафиксируем три положения равновесного состояния, когда газовый "пузырь" находится: - напротив проявляющего газового пласта с пластовым давлением рпл(рис. 1.7а); - в середине интервала от пласта до устья скважины (рис. 1.7б); - на устье (рис. 1.7в). pV=const, и давление должно оставаться неизменным, то есть р=рпл. Для верхней части давление определяется по формуле: р=рпл–ρglp а для нижней – р=рпл+ρglp где lp – расстояние от газа до заданной точки в жидкости.  Рис. 1.7. Изменение давления в герметичной скважине при всплытии газа, поступившего из вскрытого пласта. Известно, что при увеличении давления на 10 МПа объем жидкости уменьшается на 0,5%. Предположим теперь, что из пласта с давлением 30 МПа в скважину поступил газ с глубины 3000 м. Примем, что высота столба газа равна 10 м. Оказавшись на устье, газовый пузырь создает дополнительное давление на жидкость 30 МПа. Под действием такого давления жидкость сожмется на 1,5%, т.е. уровень жидкости в скважине (под газовым пузырем) "просядет" на 45 м, что в 4,5 раза больше объема газа. Очевидно, что такая предоставившаяся газу возможность расшириться приведет к уменьшению давления в газовом пузыре и равновесие наступит при значительно меньших давлениях по сравнению с ожидаемыми, полученными при расчетах без учета сжимаемости жидкости. 3. Вязкая жидкость.  (В.1) касательное напряжение в жидкости при слоистом, упорядоченном течении прямо пропорционально градиенту скорости. Коэффициент пропорциональности μ принимается за меру вязкости и характеризует это свойство жидкости.Уравнение (В.1) – это математическое выражение ньютоновской модели жидкости. Из формулы следует, что μ – это сила трения, приходящаяся на единицу поверхности трения, при градиенте скорости равном единице. Для того чтобы жидкость полностью подчинялась ньютоновской модели, необходимо, чтобы величина μ не зависела от градиента скорости du/dy. Это, в частности, означает, что с увеличением скорости жидкость и не разжижается, и не становится более вязкой. Зависимость в таких случаях графически изображается в виде прямой, исходящей из начала координат. Экспериментально полученный график зависимости называется реологической кривой или реограммой. . На рис. В.1 показаны типичные реограммы реологически стационарных систем. Прямая 1 на рис. В.1а – это типичная зависимость между τ и градиентом скорости du/dy, соответствующая модели Ньютона (В.1). |