|
Билеты по ГА. Билеты по гидре хз хз хз. 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта
Вязкопластичные жидкости.
Для трубы точным методом является уравнение Букингэма или предложенный Гродде метод решения этого уравнения. Формула Бингама по сравнению с упомянутыми методами расчета является приближенной, менее точной (как результат "отбрасывания" третьего члена в уравнение Букингэма). Если обозначить в (5.2):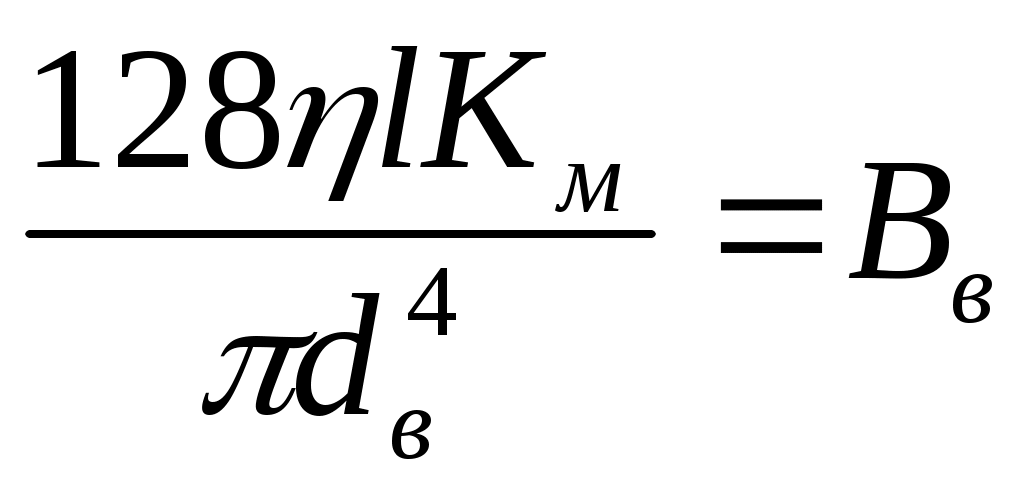 , , 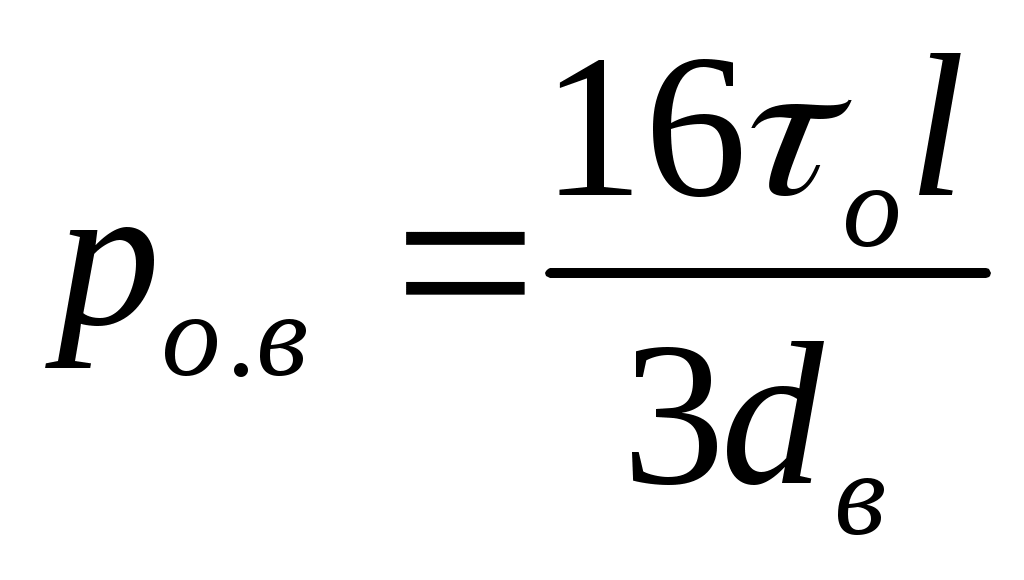 , то уравнение Бингама для трубного пространства будет иметь вид: рв =ро.в+ВвQ. Аналогично для заколонного пространства: , то уравнение Бингама для трубного пространства будет иметь вид: рв =ро.в+ВвQ. Аналогично для заколонного пространства:
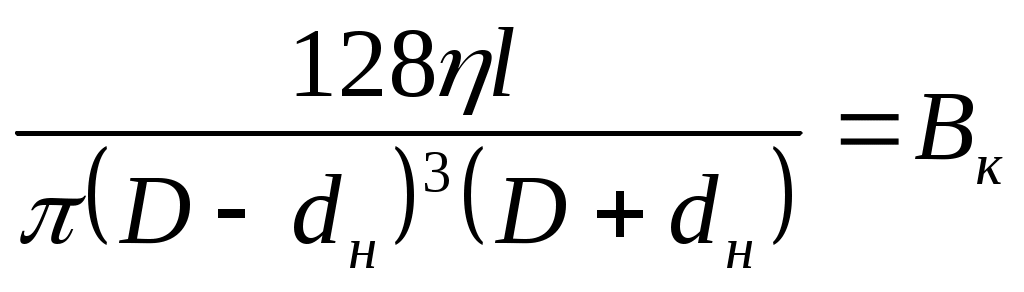 , , 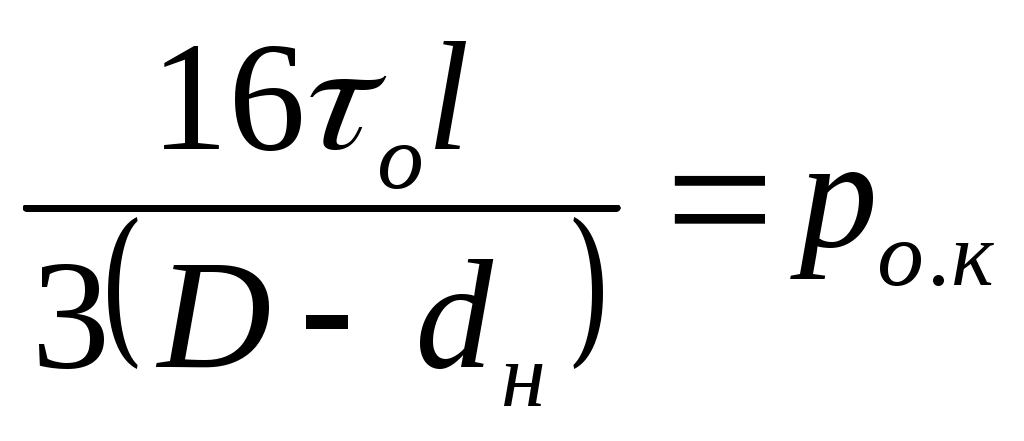 .Тогда рк =Ро.к +ВкQ . .Тогда рк =Ро.к +ВкQ .
В практике расчетов возникает часто ситуация, когда известна, например, величина рв1, соответствующая некоторому известному Q1, причем Q1 < Qкр. Чтобы получить для пересчета давлений уравнение типа (13.1), необходимо рассчитать величину ро.в. Тогда Вв найдется по формуле: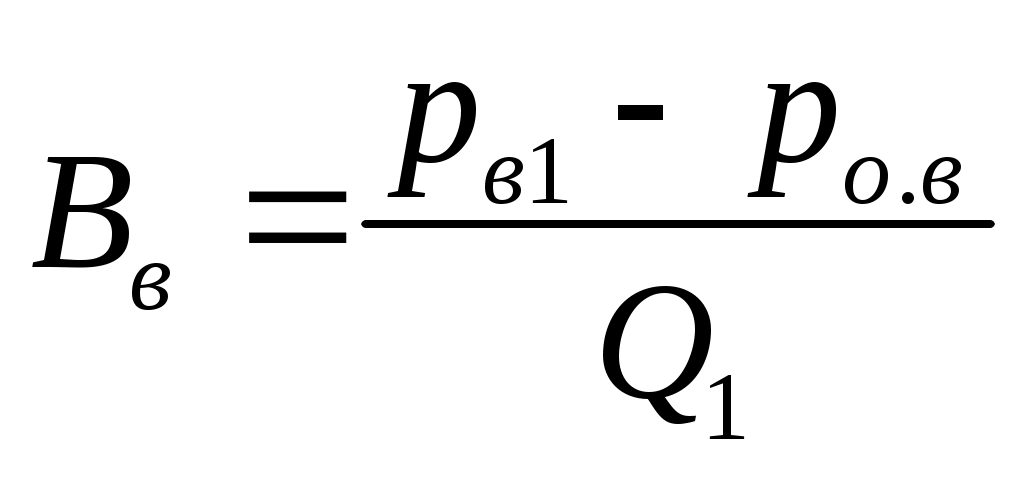 . Аналогично для кольцевого пространства: . Аналогично для кольцевого пространства: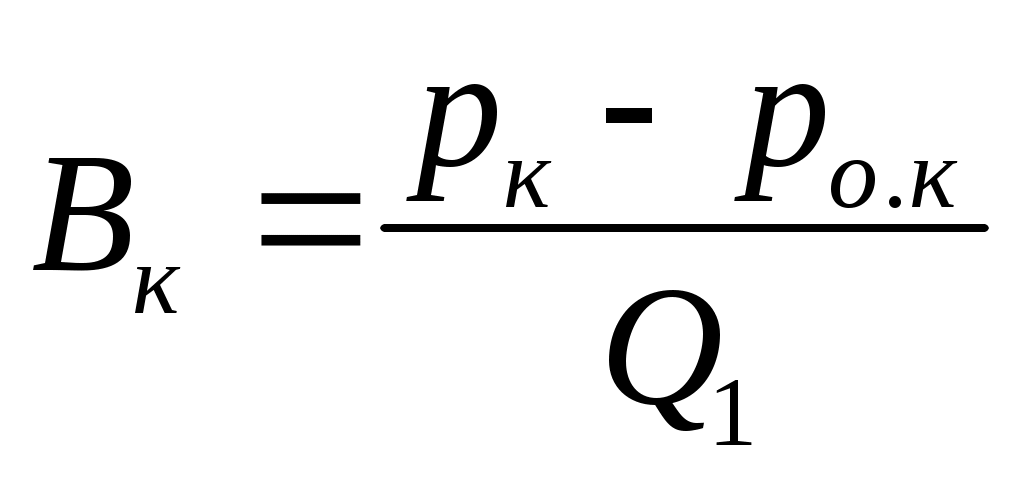 . Для долота, турбобура и манифольда потери (или перепады) давления определяются по единообразной формуле: р =АQ2, и пересчет давлений для этих элементов не сопровождается новыми погрешностями, превышающими погрешность формул. Сложнее обстоит дело с турбулентным режимом течения в доквадратичной (переходной) области, когда в формуле Дарси-Вейcбаха зависит от Q . Для ускорения пересчета рв или рк, на новое значение приходится принимать допущение (предположение): если рв1 или рк2 при Q = Q1 найдены "строгим" путем, с учетом влияния Q на , иначе говоря, с использованием формулы (6.9), то условно считается (принимается), что в окрестностях рв1 или рк2 существует квадратичная (параболическая) зависимость рв или рк от Q . Разумеется, такое допущение будет искажать результат пересчета с плюсовой ошибкой (завышать), когда Q2 > Q1, и занижать, когда Q2<Q1. Ошибка будет тем меньше, чем ближе Q к Q1 . И напротив, ошибка рв2 или рк2 будет возрастать, когда Q "удаляется" от Q1. Обобщим изложенное. Проследим за изменением вида зависимости рн =f(Q) по мере увеличения Q от малых значений до больших, соответствующих квадратичной области. Если в скважине только трубы и расход таков, что везде структурный режим, то рн=ро +(Вв+Вк)Q . Если учесть потери давления в манифольде, турбобуре и долоте, то рн=ро.в+ро.к+(Bв+Bк)Q+(Aобв+Атрб+Ад)Q2 . Если приступить теперь к увеличению Q, то в одном из элементов циркуляционной системы (скорее всего в трубах) наступит турбулентный режим, что приведет к тому, что уравнение (13.7) видоизменится: рн= ро.к+ВкQ +(Aобв+Атрб+Ад+Ав)Q2 . Если и в заколонном пространстве исчезнет структурный режим, то наступит ситуация: рн= (Aобв+Атрб+Ад+Ав+Ак)Q2 , что равноценно формуле В этом уравнении источником погрешности являются Ав и Ак, потому что в переходной области турбулентного течения они не могут считаться постоянными, поскольку: . Для долота, турбобура и манифольда потери (или перепады) давления определяются по единообразной формуле: р =АQ2, и пересчет давлений для этих элементов не сопровождается новыми погрешностями, превышающими погрешность формул. Сложнее обстоит дело с турбулентным режимом течения в доквадратичной (переходной) области, когда в формуле Дарси-Вейcбаха зависит от Q . Для ускорения пересчета рв или рк, на новое значение приходится принимать допущение (предположение): если рв1 или рк2 при Q = Q1 найдены "строгим" путем, с учетом влияния Q на , иначе говоря, с использованием формулы (6.9), то условно считается (принимается), что в окрестностях рв1 или рк2 существует квадратичная (параболическая) зависимость рв или рк от Q . Разумеется, такое допущение будет искажать результат пересчета с плюсовой ошибкой (завышать), когда Q2 > Q1, и занижать, когда Q2<Q1. Ошибка будет тем меньше, чем ближе Q к Q1 . И напротив, ошибка рв2 или рк2 будет возрастать, когда Q "удаляется" от Q1. Обобщим изложенное. Проследим за изменением вида зависимости рн =f(Q) по мере увеличения Q от малых значений до больших, соответствующих квадратичной области. Если в скважине только трубы и расход таков, что везде структурный режим, то рн=ро +(Вв+Вк)Q . Если учесть потери давления в манифольде, турбобуре и долоте, то рн=ро.в+ро.к+(Bв+Bк)Q+(Aобв+Атрб+Ад)Q2 . Если приступить теперь к увеличению Q, то в одном из элементов циркуляционной системы (скорее всего в трубах) наступит турбулентный режим, что приведет к тому, что уравнение (13.7) видоизменится: рн= ро.к+ВкQ +(Aобв+Атрб+Ад+Ав)Q2 . Если и в заколонном пространстве исчезнет структурный режим, то наступит ситуация: рн= (Aобв+Атрб+Ад+Ав+Ак)Q2 , что равноценно формуле В этом уравнении источником погрешности являются Ав и Ак, потому что в переходной области турбулентного течения они не могут считаться постоянными, поскольку: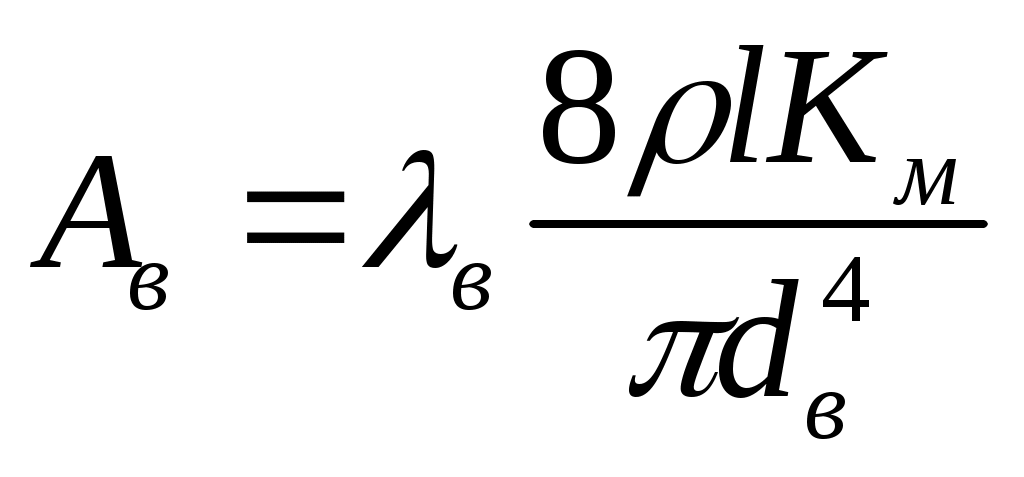 , , 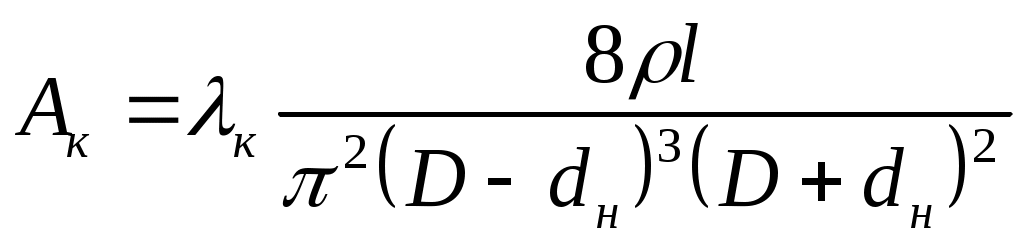 , где вик являются функциями Re*иSen , где вик являются функциями Re*иSen
На практике часто возникает ситуация, когда нужно определить А для составления уравнений типа Для этого необходимо определить "строгими" методами р, заведомо зная, что при выбранном Qрасч режим движения турбулентный, а затем найти искомое значение А: 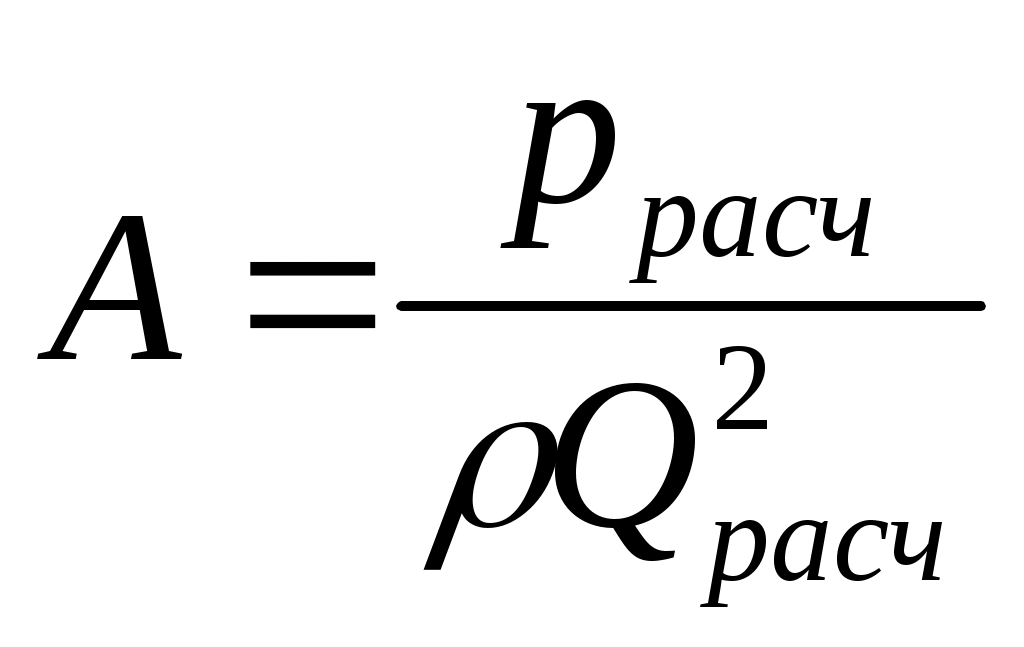 . В практике расчетов часто приходится определять Q, при котором давление на насосах, например, когда оно равно некоторому наперед заданному значению (обратная задача). Предположим, что рн ограничивается величиной рдоп. Если потери давления описываются уравнением (13.6), то искомый расход Q равен: . В практике расчетов часто приходится определять Q, при котором давление на насосах, например, когда оно равно некоторому наперед заданному значению (обратная задача). Предположим, что рн ограничивается величиной рдоп. Если потери давления описываются уравнением (13.6), то искомый расход Q равен: 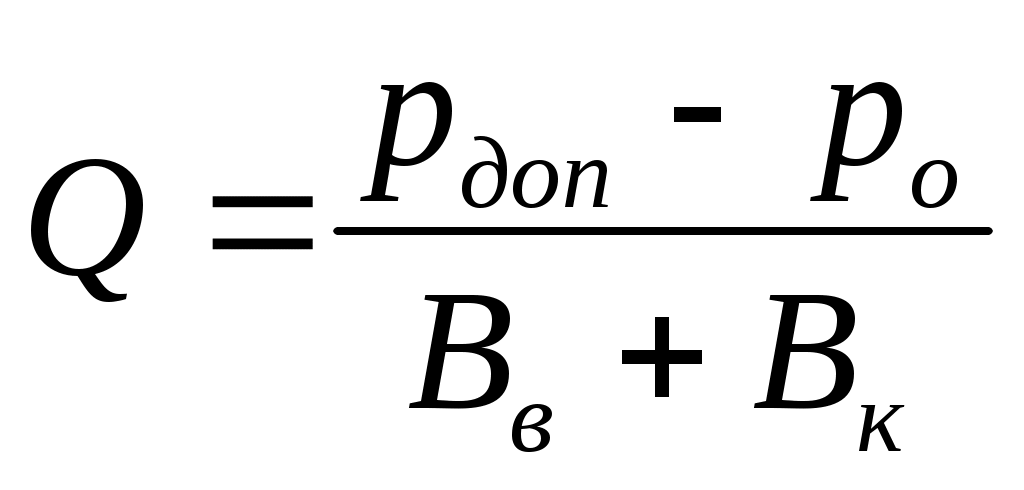 . Если функция рн =f(Q) описывается уравнением (13.5), то . Если функция рн =f(Q) описывается уравнением (13.5), то 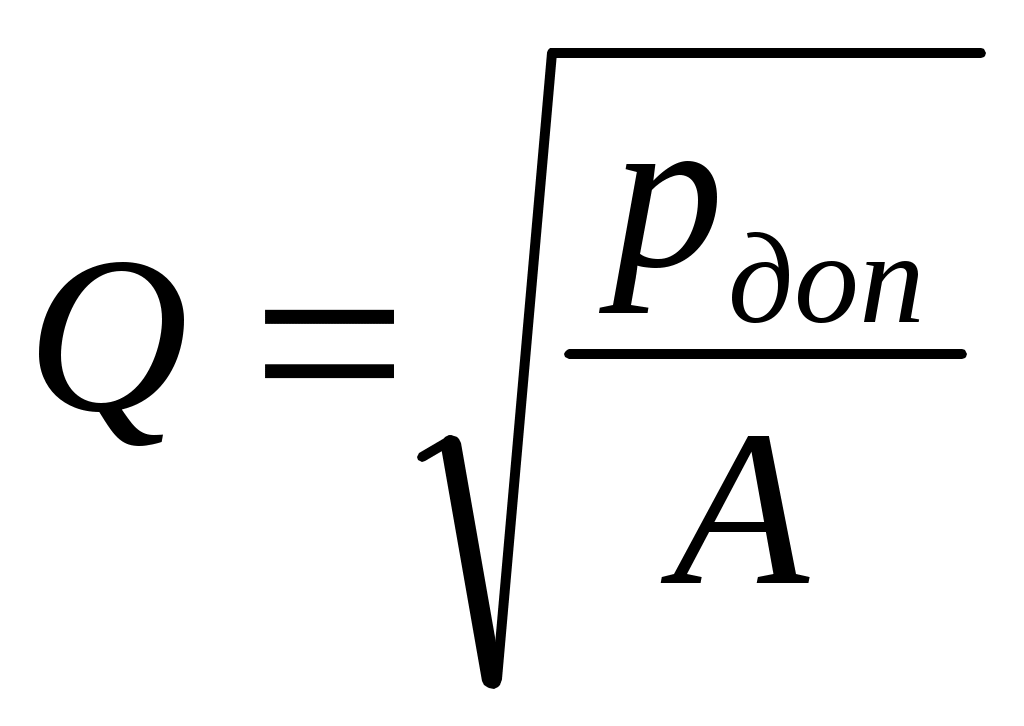 . Таким образом, при "чисто" структурном или "чисто" турбулентном режимах движения определение искомого Q выполняется достаточно просто. Сложнее обстоит дело, когда зависимости рн =f(Q) описываются уравнениями (13.7) или (13.8), когда приходится, строго говоря, искать корень полного квадратного уравнения. В таких случаях обычно прибегают к следующему допущению. Обычно сравнивают потери (или перепады) давления, относящиеся к турбулентному режиму движения, с суммой потерь давления на тех участках, где режим движения был структурным. Допущение заключается в том, что пренебрегается одной из этих сравниваемых величин. Если, например, "структурные" потери давления окажутся меньше "турбулентных", то все потери (перепады) условно относятся к турбулентным, а зависимость рн =f(Q) относят к виду (13.5). В противном случае – к виду (13.2). . Таким образом, при "чисто" структурном или "чисто" турбулентном режимах движения определение искомого Q выполняется достаточно просто. Сложнее обстоит дело, когда зависимости рн =f(Q) описываются уравнениями (13.7) или (13.8), когда приходится, строго говоря, искать корень полного квадратного уравнения. В таких случаях обычно прибегают к следующему допущению. Обычно сравнивают потери (или перепады) давления, относящиеся к турбулентному режиму движения, с суммой потерь давления на тех участках, где режим движения был структурным. Допущение заключается в том, что пренебрегается одной из этих сравниваемых величин. Если, например, "структурные" потери давления окажутся меньше "турбулентных", то все потери (перепады) условно относятся к турбулентным, а зависимость рн =f(Q) относят к виду (13.5). В противном случае – к виду (13.2).
. Псевдопластичная жидкость.
Если в одном из элементов в трубах имеет место ламинарный режим движения, то потери давления удобнее рассчитывать по формуле: р =SвQn , где 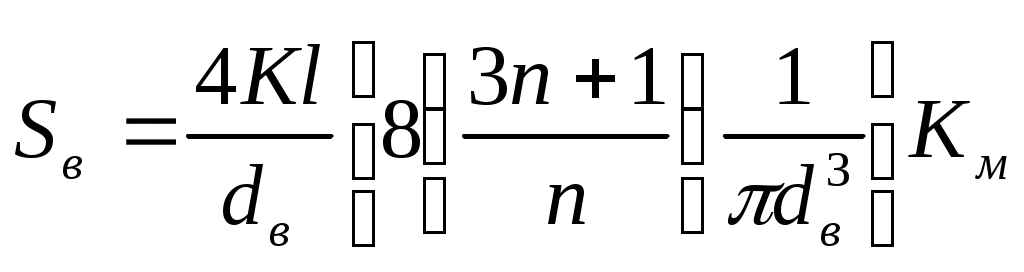 . Если решать обратную задачу, то искомый расход определяют по формуле: . Если решать обратную задачу, то искомый расход определяют по формуле: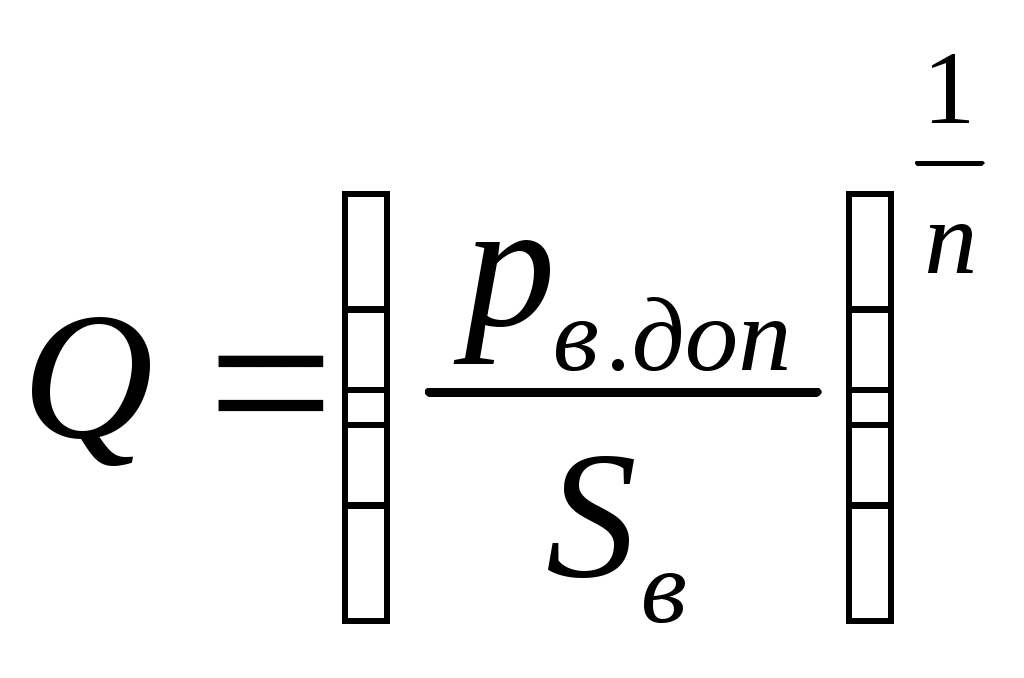 . Аналогичным образом решается задача и для затрубного пространства. При турбулентном течении расчетную формулу можно представить в виде: р =ТQ1,8 , где . Аналогичным образом решается задача и для затрубного пространства. При турбулентном течении расчетную формулу можно представить в виде: р =ТQ1,8 , где 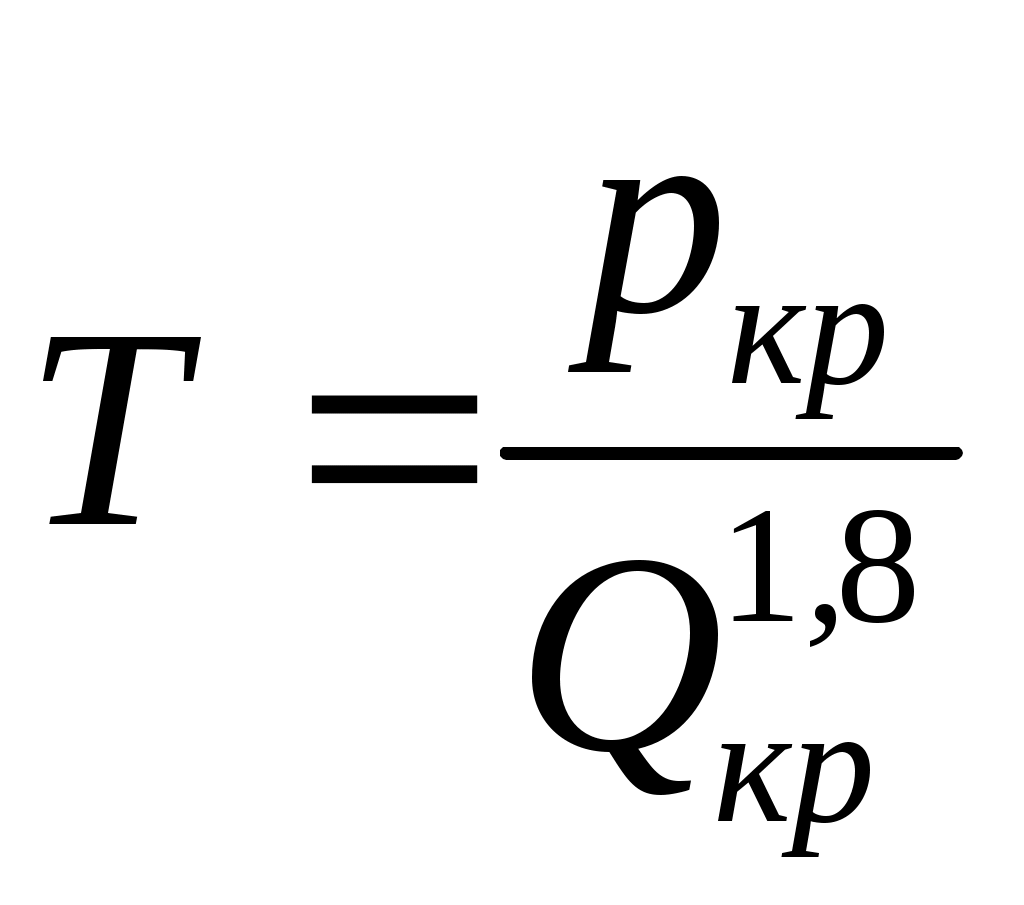 . Обратная задача решается по формуле: . Обратная задача решается по формуле: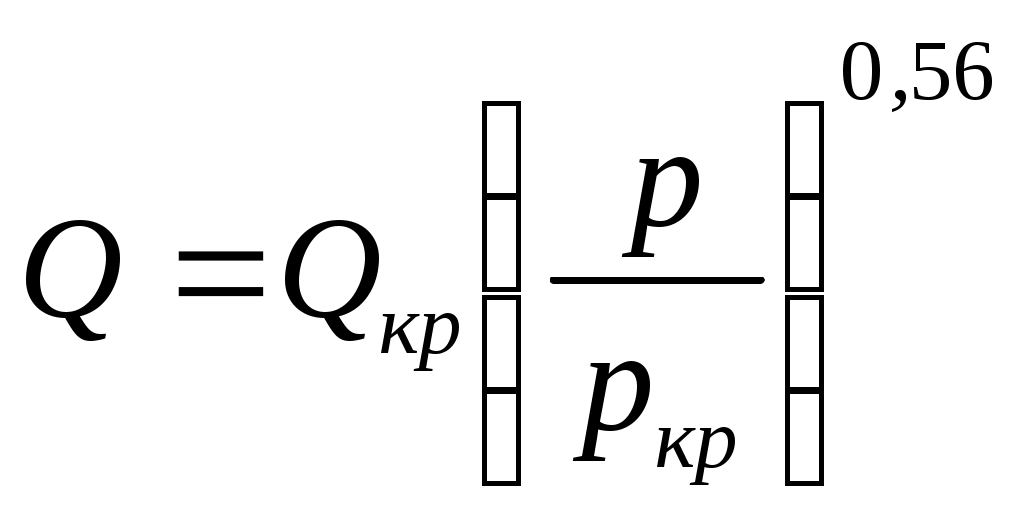 . . |
|
|
 Скачать 0.8 Mb.
Скачать 0.8 Mb.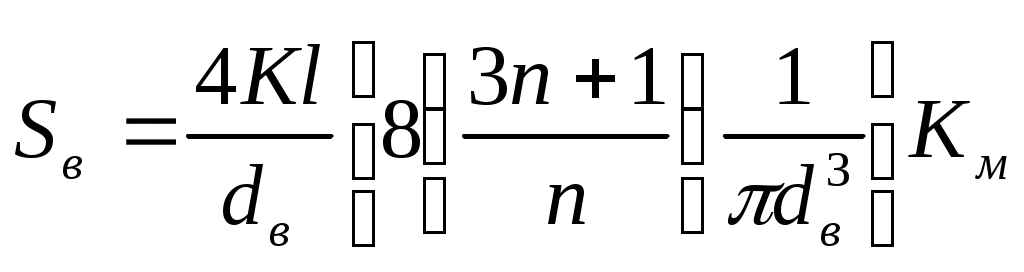 . Если решать обратную задачу, то искомый расход определяют по формуле:
. Если решать обратную задачу, то искомый расход определяют по формуле: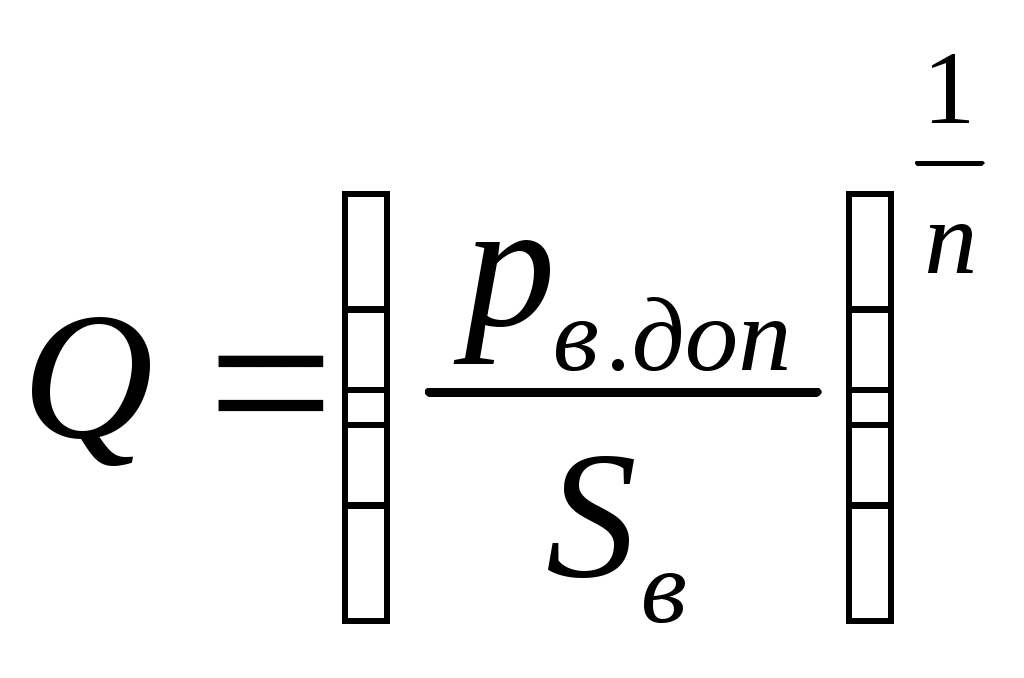 . Аналогичным образом решается задача и для затрубного пространства. При турбулентном течении расчетную формулу можно представить в виде: р =ТQ1,8 , где
. Аналогичным образом решается задача и для затрубного пространства. При турбулентном течении расчетную формулу можно представить в виде: р =ТQ1,8 , где 