Билеты по ГА. Билеты по гидре хз хз хз. 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта

• Название: 2. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта
• Анкор: Билеты по ГА
• Дата: 12.04.2022
• Размер: 0.8 Mb.
• Имя файла: Билеты по гидре хз хз хз.doc
• Тип: Документы; #466442
• страница: 2 из 10

4. Природа возникновения гидродинамических давлений при движении колонны.

Колонна труб, например, при спуске ее в скважину, движется вначале ускоренно, а затем практически равномерно. Затем наступает этап торможения до полной остановки движения. На первом и последнем этапах источником гидродинамических давлений, кроме градиента скорости в жидкости (внутреннего трения), является движение с положительным или отрицательным ускорением. Инерционная составляющая гидродинамических давлений может быть значительной, однако, как показывают натурные эксперименты, наибольшие по абсолютному значению давления соответствуют моменту равномерного движения с максимально достигнутой скоростью. Исходя из этого, в дальнейшем будем рассматривать только этот вариант движения колонны в скважине.

Предположим (рис. 14.1), что скважина представляет собой открытое с двух сторон длинное отверстие, когда жидкость, увлекаемая движущейся трубой, перемещается из верхней части в нижнюю (или наоборот). Такая схема имитирует случай спуска (подъема) колонны труб в скважину со скоростью u_тпри наличии катастрофического поглощения. Поскольку на стенке скважины скорость равна нулю, в кольцевом зазоре сформируется градиентный слой. Трубы, увлекая за собой жидкость, образуют спутный поток со средним расходом Q_ск. При этом возникает сопротивление движению труб со стороны жидкости, воспринимаемое как уменьшение веса колонны труб. 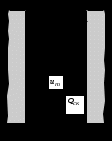Представим теперь (рис. 14.2), что та же колонна движется через круглую камеру, заполненную жидкостью. Нижняя преграда имитирует в данном случае забой скважины. В отличие от предыдущего случая здесь поток Q_ск, не имея возможности “уходить” вместе с колонной, вызывает интенсивный массообмен и образование вихреобразных циркуляционных потоков. Толщина градиентного слоя уменьшится, сами градиенты возрастут, а сопротивление движению труб увеличится.

На рис. 14.3 отображен случай спуска одноразмерной закрытой колонны в открытую, но с герметичными стенками скважину. Здесь, в отличие от предыдущих случаев, появляется новый поток Q_вт , обусловленный вытеснением жидкости из скважины трубами.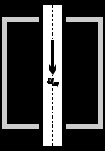




Рис. 14.2. Движение трубы через камеру, заполненную жидкостью.
Если колонна труб диаметром d_н движется вниз со скоростью u_т, то расход Q_вт равен: Q_вт =  d_н²u_т/4 . (14.1) Средняя скорость движения вытесняемого потока в заколонном пространстве определяется выражением: v_кп = Q_вт / f_кп = u_т d_н²/(D² – d_н²). (14.2) Совместно с Q_вт одновременно существует и увлекаемый трубами поток Q_ск . Для поддержания восходящего потока, занимающего к тому же не все, а только часть заколонного пространства, нужно дополнительное гидродинамическое давление.

5. Модель Шведова- Бингама.

Если реограмма представляет собой прямую (рис. В.1в), то такая жидкость называется жидкостью Бингама. Математически модель определяется уравнением: 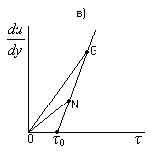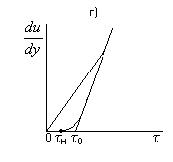. (В.5)



Шведов показал, что часть жидкостей ведет себя в соответствии с реограммой, показанной на рис. В.1г. Как видим, она состоит из двух участков: кривой (подобно модели Кэссона-Шульмана) и прямой, схожей с моделью Бингама. Для характеристики реограммы Шведова необходимо и достаточно знать три параметра: τ_н, τ_о и η. Заметим, что для модели Бингама достаточно знать τ_о и η. Обычно криволинейной частью реограммы Шведова пренебрегают, и тогда модель превращается в модель Бингама с действительной областью выше точки С. область градиента скорости от 0 до точки С считается недействительной, говоря точнее, редко встречающейся на практике. В итоге как бы объединяются две модели в одну, поэтому в технической литературе такую модель часто называют моделью жидкости Шведова-Бингама.
6. Основное уравнение гидростатики.

Поместим в скважину, заполненную вязкой жидкостью (например, глинистым раствором) так, как показано на рис. 1.2. Ось скважины направлена вертикально и параллельно оси Oz. Ось Ох направим, следовательно, горизонтально.Жидкость в точке М в герметичной скважине с координатой z будет находиться в покое в поле земного тяготения. При выбранных нами направлениях координатных осей массовая сила – сила веса будет направлена вдоль оси Оz. Следовательно, проекции массовой силы на другие оси будут равны нулю. Это значит, что в уравнении (1.1) j_x и j_y соответственно будут равны нулю, а j_z= – g.

dp=-ρgdz.

Знак "" появляется от того, что направление оси Oz не совпадает с направлением силы тяжести.

Проинтегрируем, помня о том, что для жидкости ρ=const: dp+ρgdz=0, 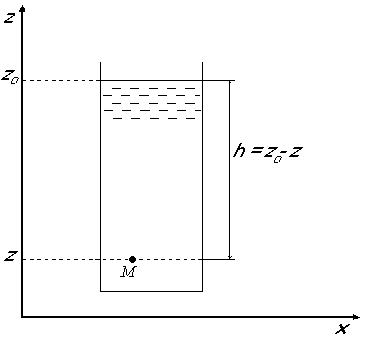. Это означает, что в общем случае , (1.2) где р_o и z_o – известное давление в точке с заданной координатой z­_o.

Рис. 1.2. К выводу основного уравнения гидростатики.
Решение (1.2) называется основным уравнением гидростатики, которое чаще представляют в виде:

р=р_o+ρg(z_o-z) (1.3)

или

р=р_o+ρgh, (1.4)

где h – глубина погружения под уровень жидкости, где давление известно.
7. Вазко-пластичная жидкость, её реограмма, параметры и реологическая функция.

Существует класс жидкостей (называемых вязко-пластичными или бингамовскими), в которых вязкое течение возникает лишь после того, как сдвиговое напряжение превзойдет некоторый предел, а до тех пор такая жидкость ведет себя как твердое тело Если предел текучести такой жидкости весьма мал, она будет вести себя как ньютоновская практически во всех реологических экспериментах, где обычно весьма трудно создать достаточно малые деформации и напряжения.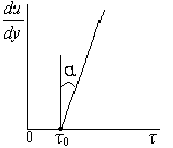

. η = _{ } – пластическая вязкость Величина τ_о называется динамическим напряжением сдвига

8. Циркуляционная система скважины, как система гидравлических сопротивлений.

Напомним, что в задаче о движении жидкостей по трубопроводу различают два вида сопротивлений: линейные и местные. Первые при всех прочих равных условиях пропорциональны длине трубопровода, а вторые отличаются тем, что приурочены к определенному месту и зависят от геометрических особенностей канала в этом месте. Сказанное является справедливым и для циркуляционной системы скважины (рис. 3.6).




Рис. 14.3. Спуск “закрытой” колонны в герметичную скважину.
Рис. 3.6. Циркуляционная система скважины.

В колонне труб, спущенных в скважину, можно выделить участки с постоянным живым сечением, например, участки равнопроходного сечения между соединениями труб. Гидравлические сопротивления на таких участках, ecтественно, являются типично линейными. Сопротивления в заколонном пространстве на участках между соединениями также являются по своей природе линейными, пропорциональными длине труб. Что касается мест соединений, то они являются источниками местных сопротивлений.

Итак, для скважины: p_н = p_л + p_м

где p_л- линейные сопротивления,

p_м- местные сопротивления.

Приведенная формула справедлива для случая, когда все сопротивления располагаются последовательно, друг за другом.

Рассмотрим типичный вариант колонны для турбинного бурения (рис.3.6).

Двигаясь вместе с жидкостью, мы встречаем следующие гидравлические сопротивления:

1. 
   в наземной обвязке буровых насосов (манифольде) на участке от насоса до бурового шланга, которые состоят из местных сопротивлений при прохождении задвижек и линейных сопротивлений по трубам обвязки, а также местных сопротивлении на соединениях труб с буровым шлангом, на изгибах (коленах) труб манифольда;
   
2. 
   в буровом шланге, где преобладают линейные сопротивления;
   
3. 
   в вертлюге, где имеют место преимущественно местные сопротивления (повороты, сужения потока, участки с резким его расширением),
   
4. 
   в ведущей трубе (рабочей трубе) - и линейные и местные (в замках);
   
5. 
   в бурильных и утяжеленных бурильных трубах - линейные (между соединениями труб) и местные - в соединениях;
   
6. 
   в турбобуре, где перепад давления складывается из перепада давления на лопатках турбины и местных потерь деления в соединениях между секциями турбобура;
   
7. 
   в промывочных отверстиях долот - это типичные местные сопротивления;
   
8. 
   в кольцевом пространстве, где сопротивления представлены набором линейных сопротивлений и местных, связанных с наличием резких сужений и резких расширений потока при прохождении замковых (муфтовых) соединений и каверн в скважине; на каждом замковом соединении (рис. 3.7) мы наблюдем три разновидности: линейное сопротивление р_мл, местное на входе в узкую часть кольцевого пространства р_мси местное сопротивление на выходе из узкой части р_мр (потери при резком расширении); влиянием каверн на потери давления обычно пренебрегают.
   

Подчеркнем ещё раз, что давление на насосах (насосе) определяется как сумма всех давлений p_i , затраченных на преодоление всех упомянутых нами сопротивлений.

9. Модель Освальда-де-Вале.Её реограмма,параметры и реологическая функция

Это степенная модель. - мера консистентности, Па·сⁿ; - показатель поведения (нелинейность),показывает на сколко отличается от прямой

10Расчёт давления в скважине,заполненной газом. Барометрическая формула.

При бурении скважин на различных этапах ее строительства, создаются ситуации, когда скважина (обычно закрытая) заполнена сжатым газом, создающим определенное давление на стенки скважины. Знание величины этого давления необходимо для расчетов обсадных колонн, оценки вероятности гидроразрыва пласта и т.п. Поэтому умение прогнозировать ожидаемые давления при возможных газопроявлениях с полным или частичным замещением жидкости в скважине газом имеет важнейшее значение.

Предположим, что закрытая скважина от кровли газоносного пласта до устья заполнена газом (рис. 1.8). Для того чтобы этот газ находился в равновесии, необходимо, чтобы столб газа создавал на пласт давление, равное давлению газа в пласте.Воспользуемся дифференциальным уравнением гидростатики.dp=ρ(j_xdx+j_ydy+j_zdz),где ρ≠const (в отличии от капельной жидкости в данном случае ρ – функция температуры и давления).Для поля земного тяготения j_x=0; j_у=0; j_z=-g, тогда dp=-ρgdz. Как отмечалось, для газа ρ=f(p,T). Для случая покоя газа в скважине можно с некоторым допущением принять процесс сжатия изотермическим, для которого p_оV_о=pV , , или отсюда . Подставив в дифференциальное уравнение гидростатики, имеем: Здесь р_о и ρ_о – известные давление и плотность в известном сечении. Разделим переменные:. Проинтегрируем:; , , где h – превышение сечения z над z_о (положительное или отрицательное). Из последнего выражения следует: отсюда (1.10) Выражение (1.10) не очень удобно для расчетов, поскольку плотность ρ_о, как правило, не известна. Воспользуемся уравнением Менделеева-Клапейрона pV_m=mR_yT, (1.11) чтобы приближенно выразить ρ_o/p_o. В уравнении (1.11): V_m – объем одного моля газа; R_y – универсальная газовая постоянная, Дж/(град^. кмоль); Т – абсолютная температура, К; т–коэффициент сжимаемости газа, показывающий отклонение поведения газа от идеального. Разделив обе части уравнения на молекулярный вес газа М и заменив p/ρ на p_o/ρ_o, получим: ; , В результате –(1.12) следовательно, подставляя (1.12) в формулу (1.10): .(1.13) Эта формула известна под именем барометрической. В расчетной практике часто свойства газов описываются с помощью коэффициента сжимаемости т и относительной плотности газа по воздуху в нормальных условиях . Для природных газов чаще используется формула: (1.14) где z-z₀=h. Для практических расчетов вполне допустимо величину принять равной 10^-4. Тогда формула (1.14) примет вид: (1.15) Формула (1.15) используется при расчете обсадных колонн в условиях газопроявлений. В известной "Инструкции по расчету обсадных колонн" она преобразована к виду: (1.16) где z_y – расстояние от устья до искомого сечения. По этой формуле можно определить давление газа на любой глубине, если известно давление газа в пласте р_пл. В частном случае, на устье скважины при z_y=0, давление равно: