основные понятия и законы гидростатики. Реферат по дисциплине Процессы и аппараты в технологии строительных материалов
 Скачать 0.73 Mb.
|
|
Министерство образования Российской Федерации Пермский государственный технический университет Строительный факультет РЕФЕРАТ по дисциплине «Процессы и аппараты в технологии строительных материалов» НА ТЕМУ: «Основные понятия и законы гидростатики» Выполнил: Проверил: Пермь 2010 Оглавление
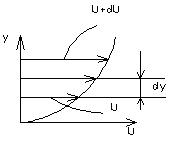
Определение жидкости. Жидкость - физическое тело, обладающее свойством текучести, т.е. способностью неограниченно изменять свою форму под действием даже весьма малых сил, но в отличие от газов практически не изменяющее свой объем при изменении давления. В обычном состоянии жидкость оказывает малое сопротивление разрыву и большое сопротивление сжатию (имеет малую сжимаемость). Вместе с тем жидкость оказывает значительное сопротивление относительному движению соседних слоев (обладает вязкостью). В понятие «жидкость» включают как жидкости обычные, называемые капельными, так и газы, когда их можно считать как сплошную малосжимаемую легкоподвижную среду. В гидравлике рассматривают только капельные жидкости. К ним относятся вода, нефть, керосин, бензин, ртуть и др. Газообразные жидкости - воздух и другие газы - в обычном состоянии капель не образуют. Основной особенностью капельных жидкостей является то, что в большинстве случаев их рассматривают как несжимаемые. Основные свойства жидкости. Рассмотрим основные физические свойства жидкости: плотность, удельный вес, температурное расширение и вязкость. 1. Плотность  - отношение массы жидкости  к занимаемому объему  : Единица плотности в системе СИ -  . Плотность воды при температуре   .Удельный вес  ( )- это вес единицы объема, т.е. где  - вес жидкости в объеме V.Для воды при имеем  .Между удельным весом и плотностью можно найти связь, если учесть что G=mg: 3. Температурное расширение. Характеризируется температурным коэффициентом  объемного расширения, представляющим собой относительное изменение объема жидкости при изменении температуры на  : где    изменение температуры,  .4. Вязкость – свойство жидкости оказывать сопротивление относительному движению (сдвигу) ее слоев. Это свойство проявляется в том, что в жидкости при ее движении между слоями возникают касательные напряжения. При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью. Скорость U уменьшается по мере уменьшения расстояния y от стенки.
 где  коэффициент динамической вязкости жидкости;  -приращение скорости, соответствующее приращению координаты  .Градиент скорости  характеризует интенсивность сдвига жидкости в данной точке, коэффициент  - вязкость капельных жидкостей и имеет размерность Нс/м2 (Па∙с).На практике наиболее часто используется коэффициент кинематической вязкости  Он измеряется в  . Для воды при   .Приборы для измерения давления. Для измерения давления используют жидкостные (барометр, пьезометр, вакуумметр, дифманометр), механические (манометр, вакуумметр) и электрические приборы. Рассмотрим принцип действия основных из них. 1. Барометр состоит из открытой чашки, заполненной ртутью, и стеклянной трубки, верхний конец которой запаян, а нижний опущен в чашку под уровень ртути. В верхней части трубки воздуха нет, поэтому в ней действует давление насыщенных паров ртути. Значение атмосферного давления определяют по формуле
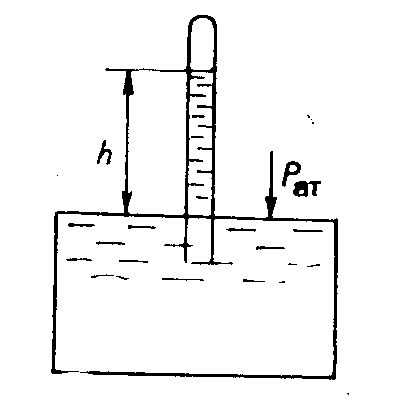
 где  - плотность ртути;  - высота подъема жидкости в трубке.2. Пьезометр - это прибор для измерения небольших давлений в жидкости при помощи высоты столба этой жидкости. Он состоит из вертикальной стеклянной трубки, верхний конец которой открыт и сообщается с атмосферой, а нижний присоединен к сосуду, в котором измеряют давление.
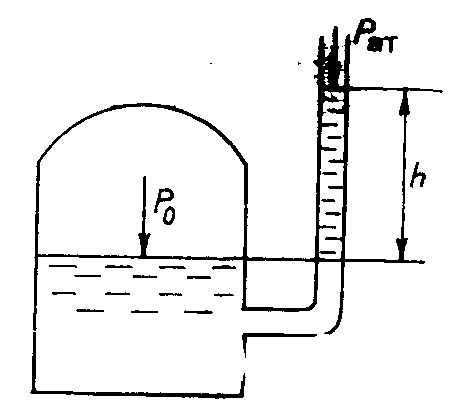
 3. Вакуумметр - это U-образная стеклянная трубка, в колене которой имеется жидкость, тяжелее от той, которая находится в сосуде. Один конец трубки соединен с сосудом, а второй открыт. Давление  на свободной поверхности жидкости, если трубка присоединена выше этой поверхности, вычисляют по формуле
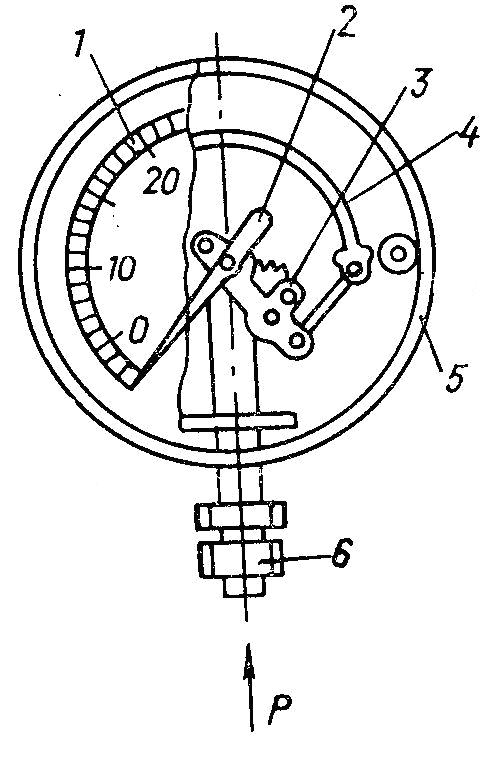
 4. Пружинный манометр состоит из корпуса 5, штуцера 6, манометрической (пружинной) трубки 4, передающего механизма 3, стрелки 2 и шкалы 1. Жидкость под давлением попадает в штуцер, а затем в трубку. Под действием давления трубка разгибается и перемещается ее свободный конец, связанный со стрелкой прибора.
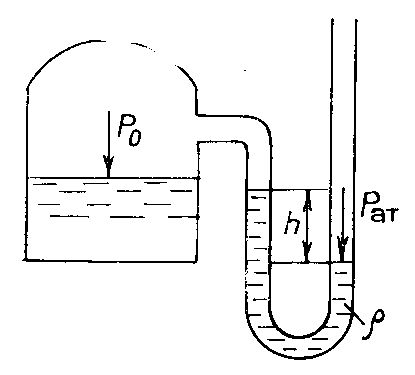
Гидростатика. В гидростатике изучается равновесие жидкостей, находящихся в общем случае, в состоянии относительного покоя, при котором в движущейся жидкости ее частицы не перемещаются друг относительно друга. При этом силы внутреннего трения отсутствуют, что позволяет считать жидкость идеальной. В состоянии относительного покоя форма объема жидкости не изменяется, и она, подобно твердому телу, перемещается как единое целое. Так, жидкость находится в относительном покое в перемещающемся сосуде (например, в цистерне), внутри вращающегося с постоянной угловой скоростью барабана центрифуги и т.д. В подобных случаях покой рассматривают относительно стенок движущегося сосуда. Жидкость в неподвижном сосуде находится в абсолютном покое (относительно поверхности земли), который в таком понимании является частным случаем относительного покоя. Независимо от вида покоя на жидкость действуют силы тяжести и давления. В случае относительного покоя следует учитывать также силу инерции переносного (вместе с сосудом) движения жидкости. Соотношение между силами, действующими на жидкость, которая находиться в состоянии покоя, определяющее условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера. В 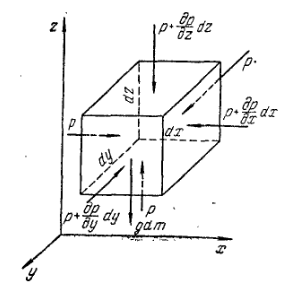 объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом  с ребрами  , и  , расположенными параллельно осям координат   и  . Сила тяжести, действующая на параллелепипед, выражается произведением его массы  на ускорение свободного падения  , т.е. равна  . Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления  на площадь этой грани. Будем считать, что давление является функцией всех трех координат:  . Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости. Рассмотрим сумму проекций на ось . Сила тяжести направлена вниз, параллельно оси . Поэтому при выбранном положительном направлении оси сила тяжести будет проектироваться на эту ось со знаком минус: Сила гидростатического давления действует на нижнюю грань параллелепипеда по нормали к ней, и ее проекция на ось равна  . Если изменение гидростатического давления в данной точке в направлении оси равно  , то по всей длине ребра оно составит . Тогда гидростатическое давление на противоположную (верхнюю) грань равно (  ) и проекция силы гидростатического давления на ось   Проекция равнодействующей силы давления на ось  Сумма проекций сил на ось равна нулю, т.е. или, учитывая, что объем параллелепипеда  (величина, заведомо не равная нулю), получим Проекции сил тяжести на оси  и равны нулю. Поэтому сумма проекций сил на ось  откуда после раскрытия скобок и сокращения находим  или  Соответственно для оси  или  Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений: 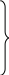 Данные уравнения представляют собой дифференциальные уравнения равновесия Эйлера. Основное уравнение гидростатики. Из дифференциальных уравнений равновесия Эйлера следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси ), оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменения давлений вдоль осей и равны нулю. В связи с тем, что в этой системе уравнений частные производные  и  равны нулю, частная производная может быть заменена на  и, следовательно Отсюда  Разделив левую и правую части последнего выражения на  и переменив знаки, представим это уравнение в виде Для несжимаемой однородной жидкости плотность постоянна и, следовательно  или  откуда после интегрирования получим  constДля двух произвольных горизонтальных плоскостей 1 и 2 последнее уравнение выражают в форме   Это и есть основное уравнение гидростатики. В данном уравнении  и 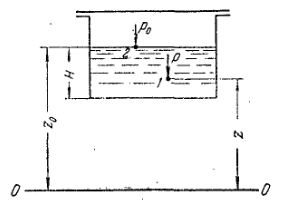 - высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), а  и  - гидростатические давления в этих точках.Р  ассмотрим, например, две частицы жидкости, из которых одна расположена в точке 1 внутри объема жидкости – на высоте от произвольно выбранной плоскости сравнения 0-0, а другая находится в точке 2 на поверхности жидкости – на высоте  от той же плоскости. Пусть и  - давления в точках 1 и 2 соответственно. При этих обозначениях, согласно основному уравнению гидростатики или  Член в уравнении гидростатики, представляющий собой высоту расположения данной точки над произвольно выбранной плоскостью сравнения, называется нивелирной высотой. Она, как и другой член этого уравнения  , выражается в единицах длины Величину называют напором давления, или пьезометрическим напором.Следовательно, согласно основному уравнению гидростатики, для каждой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная. Члены основного уравнения гидростатики имеют определенный энергетический смысл. Так, выражение члена до сокращения  характеризует удельную энергию, т. е. энергию, приходящую на единицу веса жидкости  . Аналогичный энергетический смысл получает и нивелирная высота, если ее выражение  умножить и затем разделить на единицу веса жидкости.Таким образом, нивелирная высота , называемая также геометрическим (высотным) напором, характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а пьезометрический напор – удельную потенциальную энергию давления в этой точке. Сумма указанных энергий, называемая полным гидростатическим напором, или статическим напором, равна общей потенциальной энергии, приходящейся на единицу веса жидкости.Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная. Уравнение можн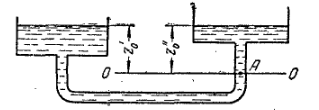о записать в форме или  П  оследнее уравнение является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, предается одинаково всем точкам его объема. Действительно, в соответствии с этим уравнением, при любом изменении давления в точке давление во всякой другой точке жидкости изменится настолько же.Принцип сообщающихся сосудов и его использование. Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью . Выберем произвольную плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то давление в данной точке Если же считать точку А принадлежащей правому сосуду, то давление в ней  (  , так как плоскость 0-0 проходит через точку А).при равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости). Следовательно,  или  Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы. Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и поперечного сечения сосудов. Этот принцип используется, в частности, для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стекол. 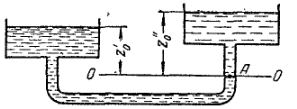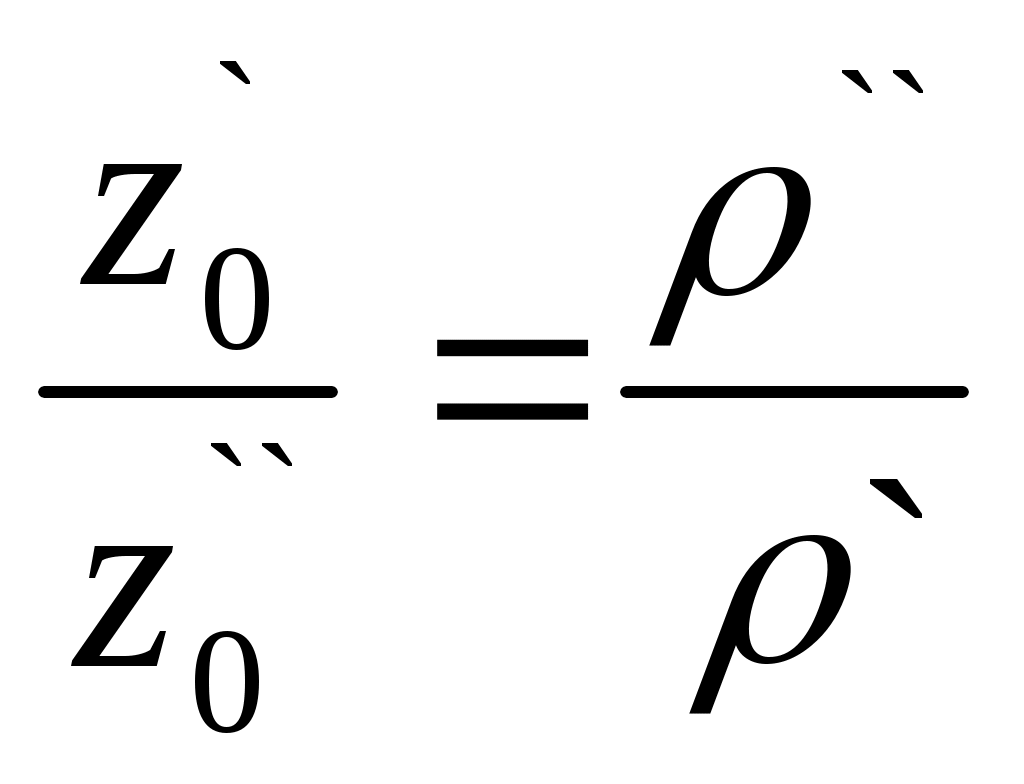Е  сли сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности  (левый сосуд) и  (правый сосуд), то при проведении плоскости сравнения 0-0 через границу раздела жидкостей аналогично предыдущему получим или  Отсюда следует, что в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей. Если сосуды заполнены одной жидкостью плотностью , но давления над уровнем жидкости в них неодинаковы и равны  (левый сосуд) и  (правый сосуд), то откуда разность уровней жидкости в сосудах  Полученное уравнение применяют при измерениях давлений или разностей давлений между различными точками с помощью дифференциальных U-образных манометров. У 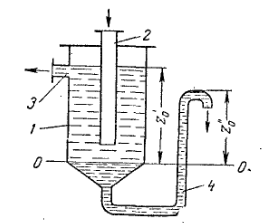 словия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах. Так, в непрерывно действующих сепараторах смесь жидкостей различной плотности (эмульсия) непрерывно поступает в аппарат 1 по центральной трубе 2 и расслаивается в нем, причем более легкая жидкость плотностью удаляется сверху через штуцер 3, а более тяжелая имеющая плотность , - снизу через U-образный затвор 4. Если принять, что уровень границы раздела фаз поддерживается на границе цилиндрической и конической частей аппарата и провести через эту границу плоскость сравнения 0-0, то необходимая высота гидравлического затвора составит При этом допускается, что давление над жидкостью внутри аппарата и на выходе из затвора одинаково. П 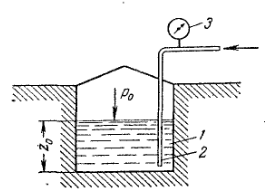 невматическое измерение количества жидкости в резервуарах. Для контроля над объемом жидкости в каком-либо резервуаре 1, например подземном, в него помещают трубу 2, нижний конец которого доходит почти до конца резервуара. Давление над жидкостью в резервуаре равно . По трубе 2 подают сжатый воздух или другой газ, постепенно повышая его давление, замеряемое манометром 3. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление , фиксируемое манометром, перестанет возрастать и будет равно откуда уровень жидкости в резервуаре  П 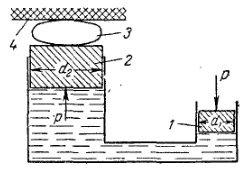 о величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.Гидростатические машины. На использовании основного уравнения гидростатики основана работа гидростатических машин, например гидравлических прессов, применяемых в химической промышленности для прессования и брикетирования различных материалов. Если приложить относительно небольшое усилие к поршню 1, движущемуся в цилиндре меньшего диаметра  , и создать давление на поршень, то согласно закону паскаля, такое же давление будет приходиться на поршень 2 в цилиндре большего диаметра  . При этом сила давления на поршень 1 составит а сила давления на поршень 2  В результате поршень в цилиндре большего диаметра передает силу давления, во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, во сколько поперечное сечение цилиндра 2 больше, чем цилиндра 1. Таким способом с помощью сравнительно небольших усилий осуществляют прессование материала 3, помещенного между поршнем 2 и неподвижной плитой 4. Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех его точках горизонтального дна сосуда одинаково, давление же на его боковые стенки возрастает с увеличением глубины погружения. Гидростатическое давление на уровне дна сосуда, как и для любой точки внутри жидкости, определяется уравнением , но для всех точек дна величина  представляет собой высоту жидкости в сосуде. Обозначив последнюю через  , получим таким образом, сила давления  на горизонтальное дно сосуда не зависит от формы сосуда и объема жидкости в нем. При данной плотности жидкости эта сила определяется лишь высотой столба жидкости и площадью  дна сосуда: или  Гидростатическое давление жидкости на вертикальную стенку сосуда изменяется по высоте. Соответственно сила давления на стенку также различна по высоте сосуда. Поэтому  где - расстояние от верхнего уровня жидкости до центра тяжести смоченной площади стенки.В данном уравнении выражение в скобках представляет собой гидростатическое давление в центре тяжести смоченной площади стенки. Поэтому сила давления на вертикальную стенку равна произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки. Точка приложения равнодействующей сил давления на стенку называется центром давления. Эта точка расположена всегда ниже центра тяжести смоченной площади. Если давление передается жидкостью в одинаковой степени каждому элементу стенки, независимо от глубины его погружения, и, следовательно, равнодействующая сила этого давления приложена в центре тяжести стенки, то давление столба жидкости на стенку тем больше, чем глубже расположен соответствующий ее элемент. В результате, в частности, для вертикальной прямоугольной стенки центр давления расположен на расстоянии  от верхнего уровня жидкости.Список используемой литературы Касаткин А.Г. Основные процессы и аппараты химической технологии / Москва, 2004г. Башта Т.М., Руднев С.С., Некрасов Б.Б. Гидравлика, гидромашины и гидроприводы / 1982г. Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии / Москва, 1962г. |
