Билет 1.
Легкоподвижность (текучесть) жидкой среды. В чем она проявляется?
Легкоподвижность – свойство среды неограниченно деформироваться под действием постоянной сколь угодно малой силы. Она проявляется в том, что ж. и г. принимают форму той области пространства, которую занимают.
2. Давление жидкости на твердые поверхности. Тело давления и закон Архимеда.
Определим силу давления на твёрдое тело, погружённое в жидкость. На замкнутую криволинейную поверхность, являющуюся поверхностью твердого тела погружённого в жидкость будут действовать массовые силы (в данном случае силы тяжести) и поверхностные, силы давления на поверхность тела. Рассмотрим действие сил давления. Как известно, горизонтальные составляющие силы давления будут взаимно уравновешены. Так как проекции тела на координатную плоскость XOZс его левой и правой сторон совпадут; то совпадут и координаты центров тяжести этих проекций. Тогда проекции сил давления на ось ОХ будут одинаковыми по величине, но противоположными по направлению Аналогично на проекции поверхностей в координатной плоскости YOZ),. Неуравновешенными будут лишь вертикальные составляющие силы давления, действующие на верхнюю и нижнюю стороны поверхности тела. Вертикальными сечениями выделим на верхней и нижней половинах тела малые площадки. Тогда вертикальные составляющие на верхнюю и нижнюю площадки будут равны:
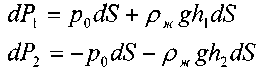
После интегрирования по объёму тела найдём равнодействующую сил давления. Она окажется равной разности весов двух тел давления, ограниченных свободной поверхностью жидкости и верхней и нижней поверхностями тела.
Таким образом, сила давления покоящейся жидкости на погруженное в нее тело направлена вертикально вверх и равна весу жидкости в объеме тела. Этот результат составляет содержание закона Архимеда: сила А называется архимедовой или гидростатической подъемной силой. Если G – вес тела, то его плавучесть определяется соотношением сил А и G. При 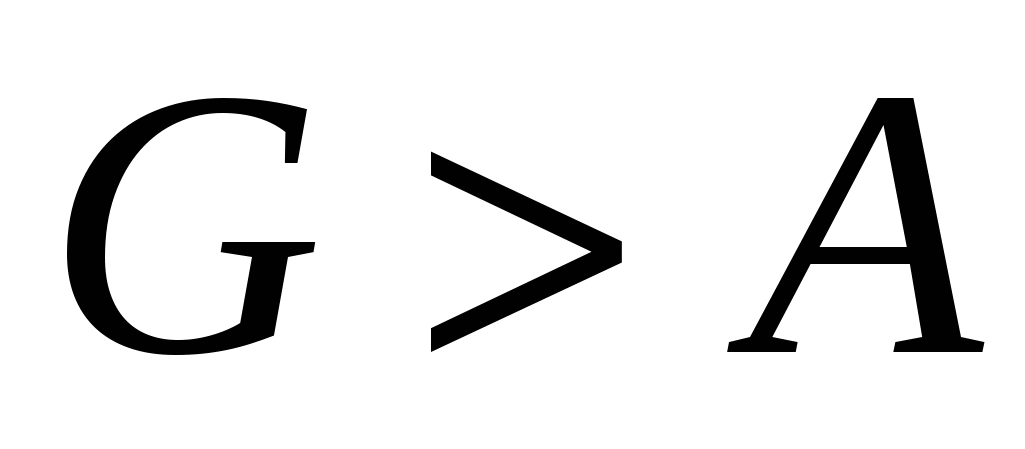 тело тонет, при тело тонет, при 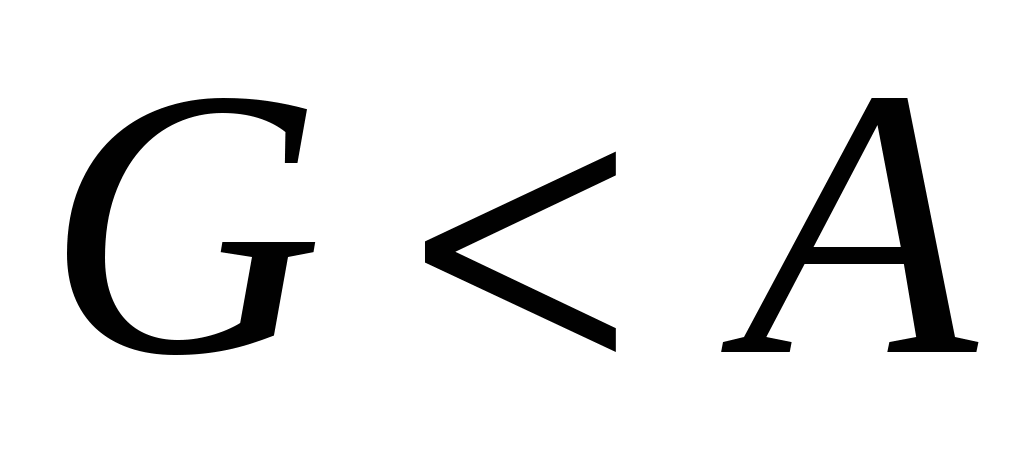 – всплывает, при G = А – плавает в состоянии безразличного равновесия. Следует иметь в виду, что линии действия сил G и А могут не совпадать, так как линия действия веса G проходит через центр тяжести тела, а линия действия архимедовой силы А – через центр его объема. При неравномерном распределении плотности тела может появиться момент, способствующий опрокидыванию тела. – всплывает, при G = А – плавает в состоянии безразличного равновесия. Следует иметь в виду, что линии действия сил G и А могут не совпадать, так как линия действия веса G проходит через центр тяжести тела, а линия действия архимедовой силы А – через центр его объема. При неравномерном распределении плотности тела может появиться момент, способствующий опрокидыванию тела.
Степень погружения плавающего на поверхности тела под уровень жидкости зависит от со отношения плотности тела и жидкости: 
Тело давления - объем жидкости, лежащий над криволинейной поверхностью, между вертикальными плоскостями, проходящими через крайние образующие и свободной поверхностью жидкости или ее продолжением.
3. Гипотеза сплошности среды. Основные понятия жидкого континуума.
Указанные обстоятельства позволяют ввести гипотезу сплошности изучаемой среды и заменить реальные дискретные объекты упрощенными моделями, представляющими собой материальный континуум, т. е. материальную среду, масса которой непрерывно распределена по объему, т.е. жидкость можно рассматривать как сплошную среду (континуум), лишенную молекул и межмолекулярных пространств. Гипотеза сплошности среды означает, что всякий малый элемент объема жидкости считается все-таки настолько большим, что содержит еще очень большое число молекул.
Согласно гипотезе сплошности масса среды распределена в объеме непрерывно и в общем неравномерно.
Реально существующее хаотическое движение молекул отражается в этом случае в величине макроскопических параметров - P T W, которые для континуума являются функциями точек пространства.
Для газа используют критерий Кнудсена: Kn = l / L, где l – длина свободного пробега молекул, L – характ. размер течения.
1. Kn < 0,01 то гипотеза сплошности справедлива.
2. Kn > 0,01 то течения разреженных газов. В этой области различают три степени разреженности: (0,01- 0,1) – течения со скольжением; (0,1- 10) – переходная, наименее исследованная область течения разреженных газов; (>10) – свободномолекулярное течение.
Жидкий объем – это мысленно выделенный в жидкости малый или конечный объем, состоящий из одной или из одних и тех же частиц, которые при движении может деформироваться, но масса жидкости, заключенная в нем не изменяется и не смешивается с окружающей средой.
Контрольный объем – это мысленно выделенный постоянный объем, занимающий неизменное положение в пространстве (ч/з к.о. протекает жидкость).
Контрольная поверхность – это поверхность, ограничивающая контрольный объем (для жидкого объема – поверхность жидкого объема)..
Внешняя или окружающая среда – жидкость и все остальное, находящееся вне выделенного объема.
Жидкий контур – контур в пространстве, состоящий из одних и тех же жидких частиц.
Скорость жидкости в данной точке – мгновенная скорость движения центра массы жидкой частицы, проходящей в данный момент через данную точку пространства.
Билет 8.
1. Эквивалентная шероховатость: физический смысл и принцип определения.
Характер шероховатости зависит от материала стенок труб, степени обработки, а последние определяют высоту выступов, их густоту и форму. Для приближенной оценки введено понятие средней высоты бугорков (выступов) шероховатости, называемой абсолютной шероховатостью и обозначаемой k. Очевидно, что чем меньше диаметр, тем быстрее частицы жидкости совершат пробег от центра трубопровода к стенкам и встретятся с бугорками шероховатости, и, отражаясь от них, вызовут возмущения в потоке жидкости. Следовательно, частота вихреобразования при малых диаметрах труб больше, и шероховатость той же высоты проявляется сильнее. Поэтому введено понятие относительной шероховатости, т. е. отношение абсолютной шероховатости к диаметру трубы 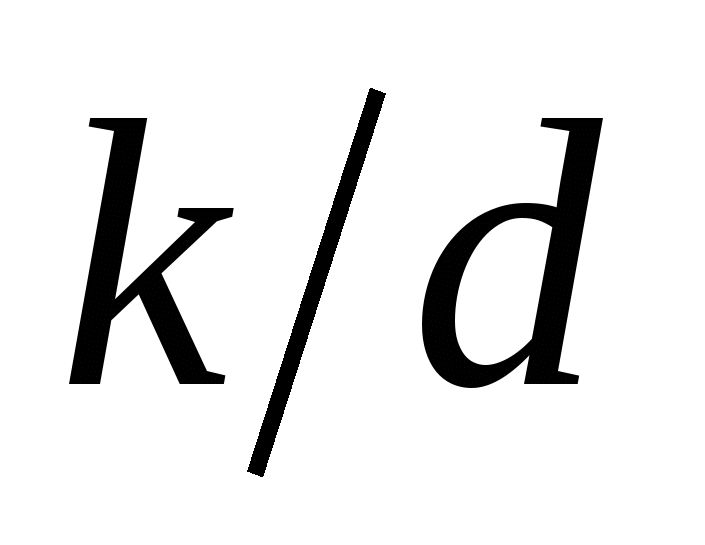 . .
Так как на характер сопротивлений оказывает влияние не только относительная шероховатость, но и форма и распределение выступов по поверхности, то в практику расчетов было введено понятие об эквивалентной равнозернистой шероховатости kэ. Под ней понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает при подсчетах одинаковое с заданной шероховатостью значение коэффициента гидравлического трения  . .
3. Картина стабилизации течения при ламинарном течении вязкой несжимаемой жидкости в трубе.
Участок от начала трубы, на котором формируется (стабилизируется)параболический профиль скоростей, называется начальным участком течения. Область, в котором имеет место поперечный градиент скорости и действуют связанные с ними касательные напряжения называют, пограничным слоем.
Если жидкость из какого-либо резервуара поступает в прямую трубу постоянного диаметра и движется по ней ламинарным потоком, то распределение скоростей по сечению трубы вблизи входа получается практически равномерным. Но затем под действием сил вязкости происходи перераспределение скоростей по сечениям: слои, прилежащие к стенке, тормозятся, а центральная часть потока (ядро), где еще сохраняется равномерное распределение скоростей, движется ускоренно, что обусловлено необходимостью прохода через неизменную площадь определенного расхода жидкости
Для определения длины начального участка можно пользоваться приближенной формулой Шиллера, выражающей длину, отнесенную к диаметру трубы, как функцию числа Re: lнач/ d = 0.029Re.
Сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значением производной dv/dy у стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше касательные напряжения, определяемые законом ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т.е. чем меньше координата x.
Билет 12.
1. Число λ и диапазон его измерения.
Приведенная скорость λ = W/ aкр– отношение скорости потока к критической скорости звука.
W=0 λ=0
W=Wmax 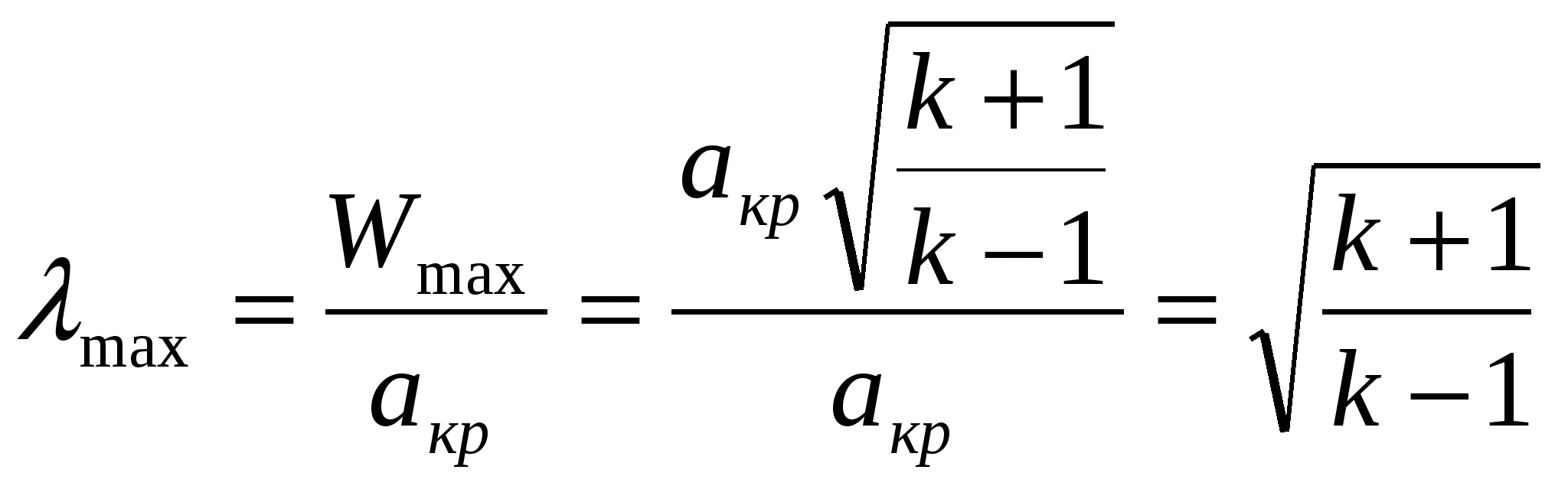
3.12 Принципы расчета пограничного слоя.
Способы расчета пограничного слоя:
1. Решается система дифференциальных уравнений.
2. Метод приближенного анализа. В этом случае ограничиваются отысканием решения удовлетворяющего уравнению сохранения для пограничного слоя в целом (интегральные соотношения) и граничным условием на стенке и на внешней границе пограничного слоя. При этом необходимо дополнительно задавать профили скорости, а в общем случае и температуры, что является недостатком метода Преимущества: простота, наглядность, универсальность.
3. Комбинированный
Билет 13.
1. Параметры заторможенного потока.
Для идеальной адиабаты:  ; ; 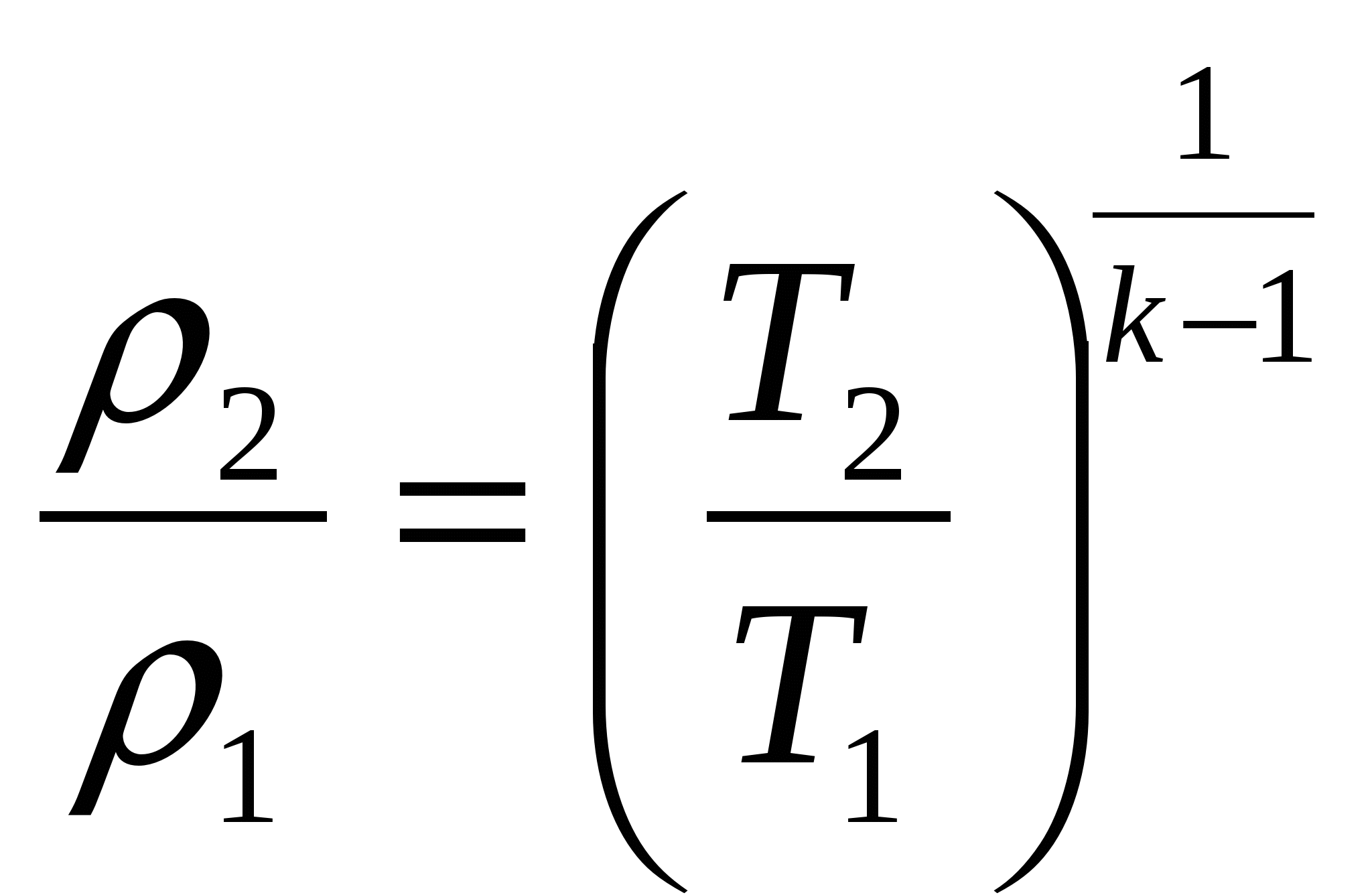
При полном энергетически изолированном и изоэнтропном торможении до W=0 все параметры примут значения параметров торможения:
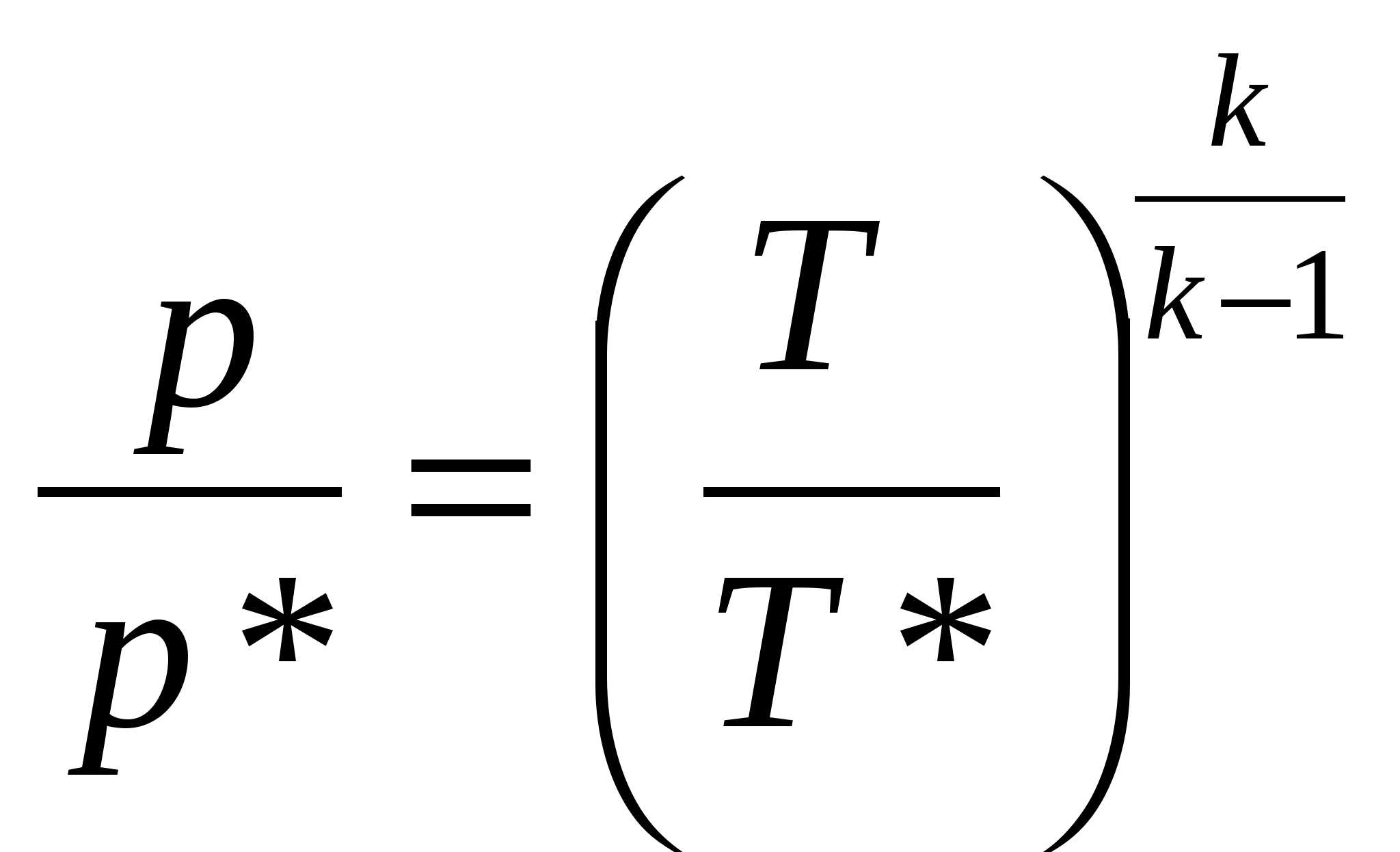 ; ;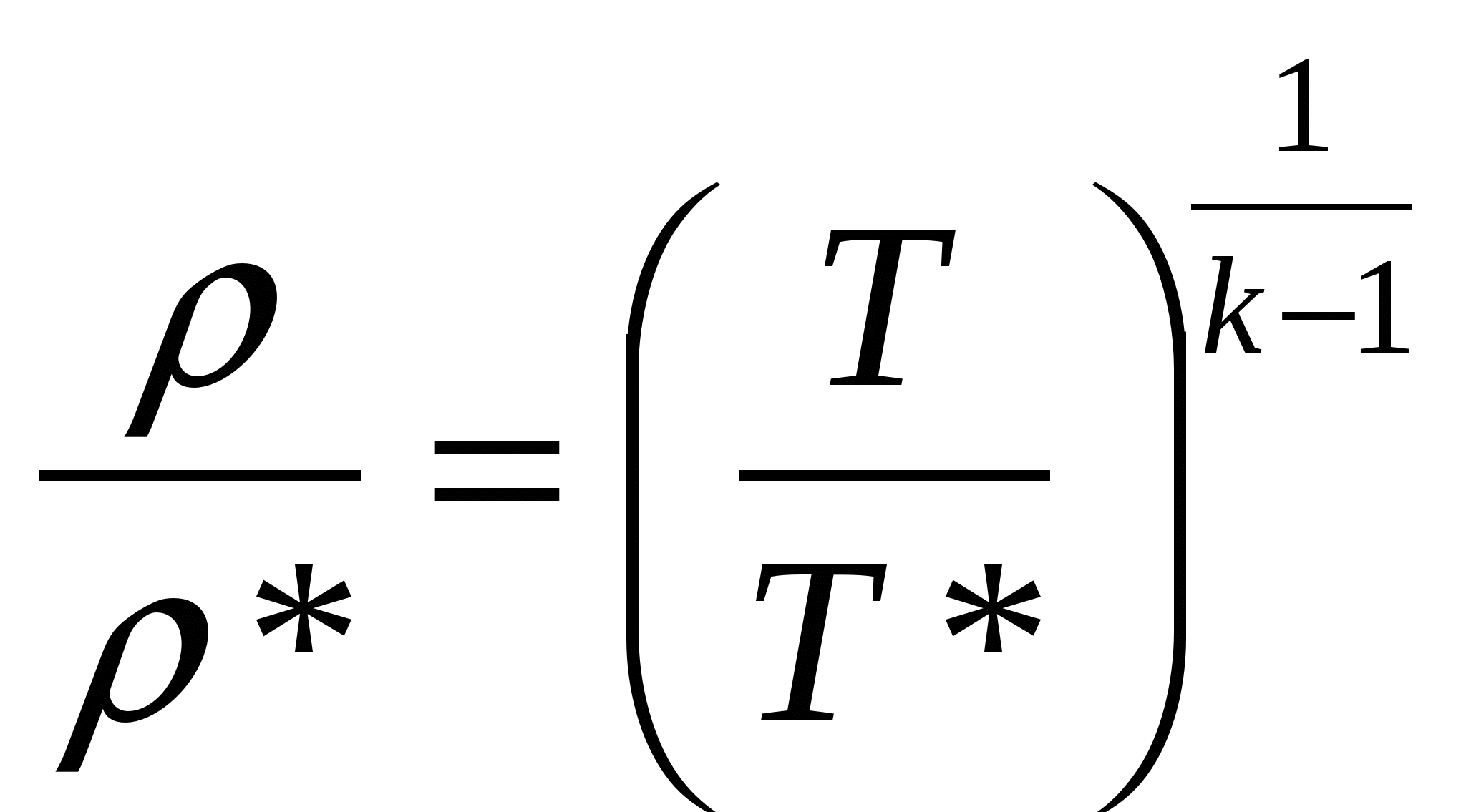 . Тогда . Тогда 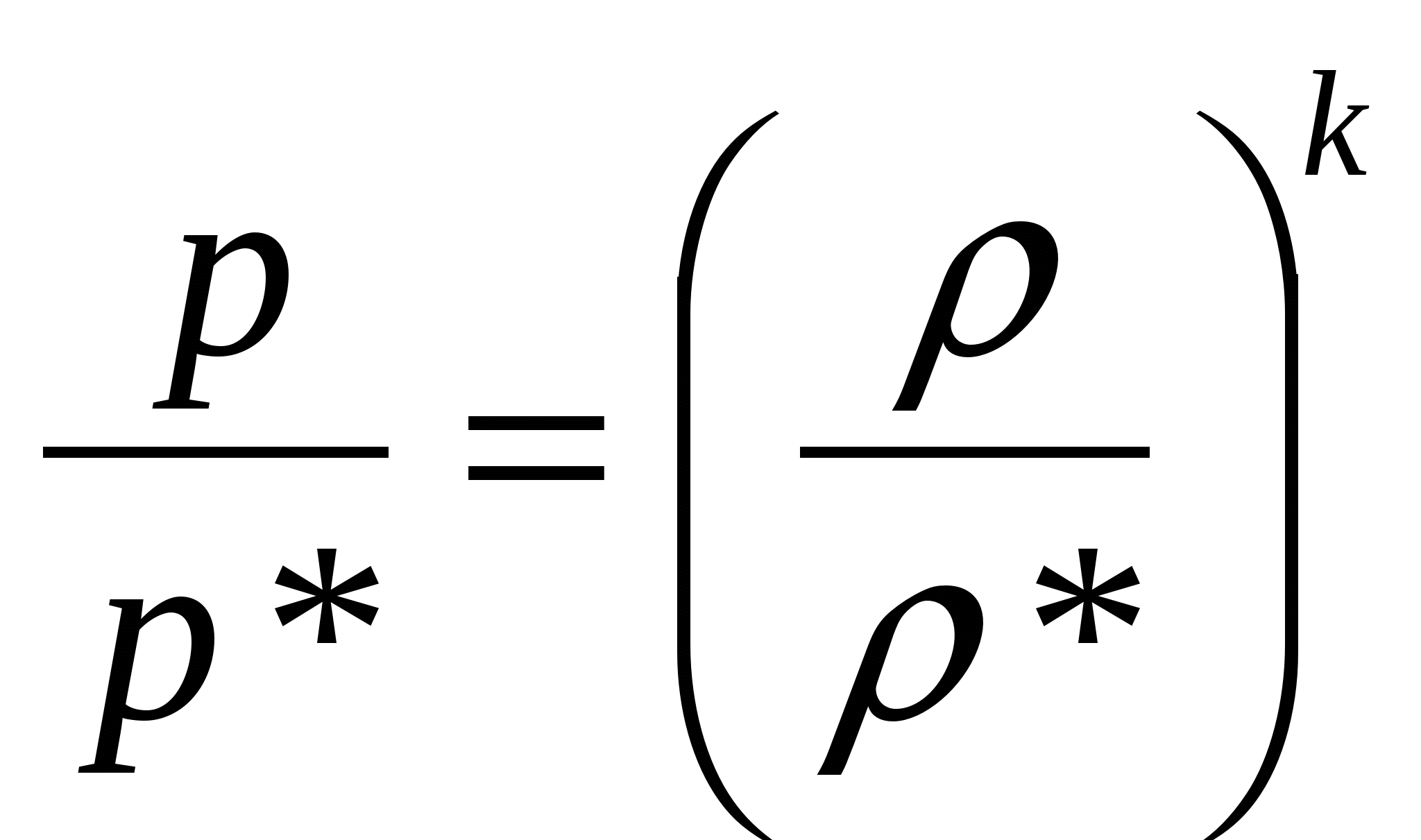
Т.о. уравнение изоэнтропы справедливо и для параметров торможения: 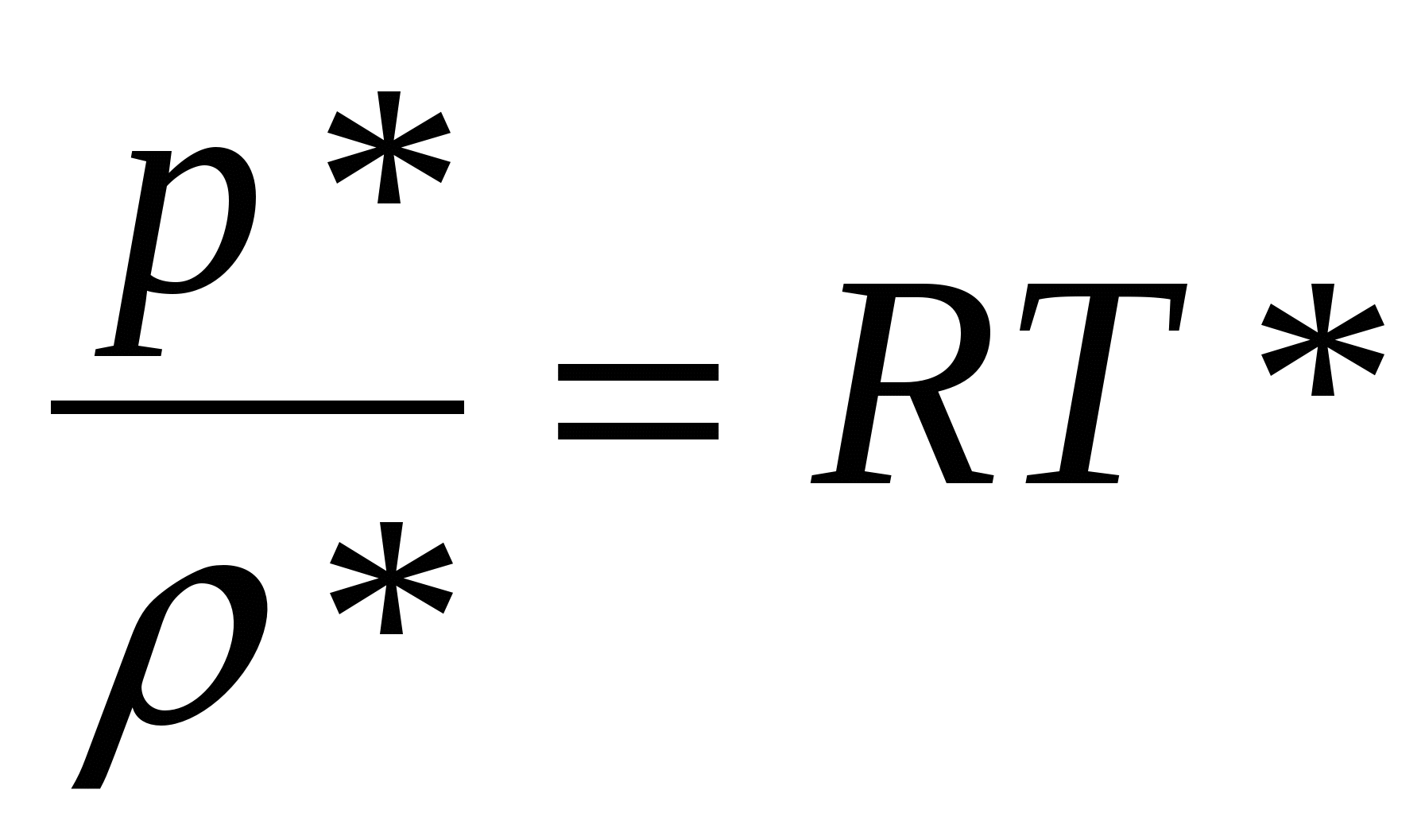 . .
Величина i*= i+ W²/2 называется полной энтальпией (энтальпией заторможенного потока) и состоит из потенциальной (i= u+p/) и кинетической (W²/2) энергией газа.
Полной энтальпии соответствует полная температура, которая называется температурой торможения: T*=i*/Cp = T+W²/2 Cp .
2. Трубопровод с насосной подачей жидкости.
Насосная подача жидкости в авиационной и ракетной технике наиболее распространенна вследствие ее надежности, хороших характеристик и минимального веса.
Схема работы: насос подает топливо из бака к двигателю, где оно впрыскивается через форсунку с большой скоростью в камеру сгорания. Часть трубопровода до насоса называется всасывающей, а за насосом – нагнетающей или напорной.
Всасывающий насос. Процесс всасывания, осуществляемый насосом, создающим пониженное давление p10, обеспечивается давлением p0 в баке. Давление p0 расходуется на подъем топлива на высоту z1, сообщение ему кинетической энергии, преодоление всех гидравлических сопротивлений всасывающего трубопровода и сохраняется в виде давления p1, которое должно обеспечивать бескавитационую работу насоса. Если бак сообщается с атмосферой, то при увеличении высоты полета давление p0 уменьшается, а вместе с ним и p1, что ограничивает высотность системы ввиду возможности возникновения кавитации. Для расчета всасывающего трубопровода используется уравнение:

Потребный напор – это напор, который необходимо сообщить одному килограмму топлива в насосе для обеспечения заданных параметров работы системы.  . Уравнение является характеристикой всего трубопровода. . Уравнение является характеристикой всего трубопровода.
Работу, которую насос сообщает жидкости или полезную работу можно подсчитать по уравнению Бернулли, составленного для участка 1-2 при условии постоянного диаметра, u, z:
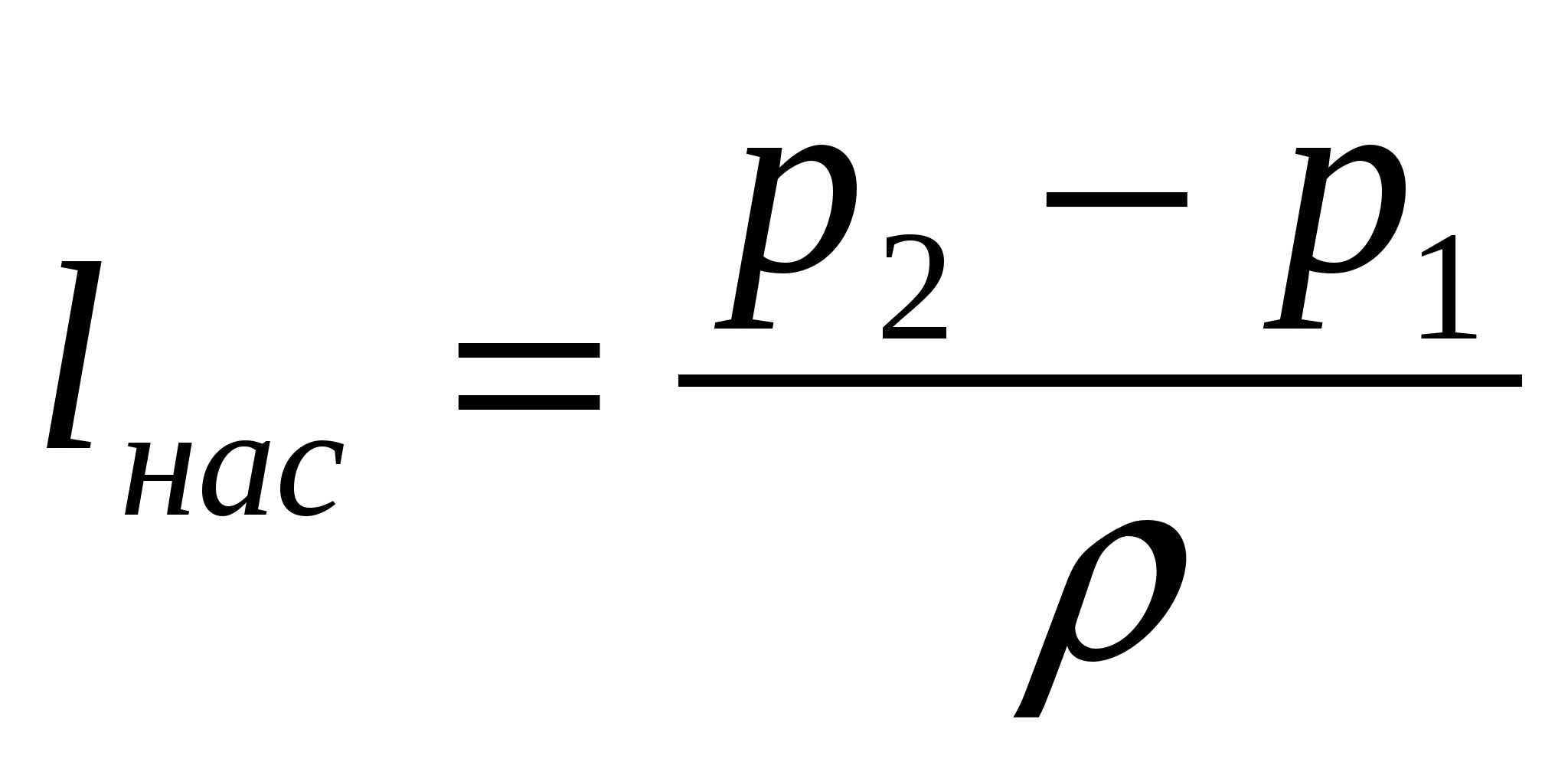 . Работа насоса заключается в повышении давления топлива. . Работа насоса заключается в повышении давления топлива.
Характеристика насоса – это зависимость полезной работы насоса от расхода жидкости Hнас = f2(Q) при постоянной частоте вращения вала насоса. Установившийся режим работы гидравлической системы с насосной подачей определяется точкой пересечения характеристики трубопровода Hпотр=f(Q) и характеристики насоса Ннас=f2(Q), которая называется рабочей точкой и соответствует условию Hпотр= Ннас. Во время работы такой режим устанавливается т поддерживается автоматически. Режимы работы двигателей и вместе с ними расходы топлива изменяются в широком диапазоне. Поэтому топливные системы снабжаются системами регулирования, позволяющими смещать рабочие точки на меньшие и большие расходы.
Замкнутый трубопровод с насосной подачей применяется в системах охлаждения и смазки двигателей или каких-либо объектов.
3. Сравнение характеристик ЛПС и ТПС при обтекании плоской стенки.
Течение в ПС на стенке может быть ламинарным, переходным и турбулентным, независимо от течения невозмущенного потока. Характерные величины: толщина пограничного слоя =d/2 и скорость внешнего потока Wн =Wmax , то переход ламинарного течения в турбулентное будет также определяться критическим числом Рейнольдса: Re=Wl/ = (2,8…30)*1000.
На малых расстояниях от передней кромки пластины толщина пограничного слоя мала и в пограничном слое сохраняется устойчивое ламинарное течение с молекулярным механизмом переноса. При увеличении толщины ламинарного пограничного слоя до критической величины на расстоянии Xкр устойчивость ламинарного течения в ПС нарушается и появляется участок переходного течения, где хаотически во времени сменяются ламинарный и турбулентный режимы течения. За переходным участком начинается турбулентный пограничный слой с турбулентным механизмом переноса. Характерным признаком перехода является резкое увеличение толщины пограничного слоя и напряжения трения на стенке. Длина переходного участка не велика.
Билет 17.
1. Струйные течения. Основная особенность струйных течений на поверхности раздела двух сред.
Свободной струей называется поток, не ограниченный твердыми стенками. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.
Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.
Свойства потока при плавно изменяющемся движении: 1. поперечные сечения потока плоские, нормальные к оси потока; 2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. 3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.
При движении потока между жидкостью и стенками, ограничивающими поток, возникают силы сопротивления. Кроме того, вследствие вязкости жидкости между ее отдельными слоями возникают силы сцепления, которые также затормаживают движение потока. Скорость движения частиц жидкости уменьшается по мере по мере удаления от оси потока к стенкам трубы, лотка и т. д. Равнодействующая сил сопротивления параллельна оси потока и направлена в сторону, противоположную направлению движения.
Для преодоления сил гидравлического трения и сохранения поступательного движения жидкости необходимо приложить силу, направленную в сторону движения и равную силам сопротивления.
2. Опытные данные о коэффициенте гидравлического сопротивления в трубах.
В 1930-1933гг. Никурадзе провел систематические опыты в трубах с искусственной равномерной зернистой шероховатостью из кварцевого песка.
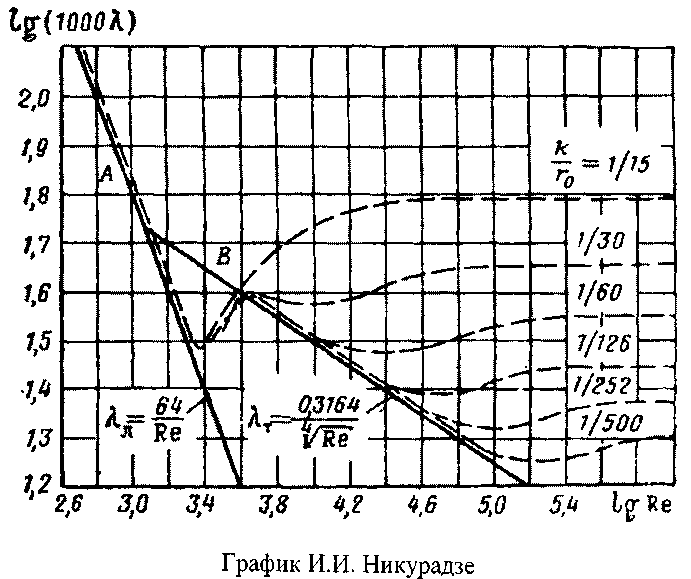
На графике зависимости легко различимы все четыре области течения жидкости.
I ламинарное течение жидкости (прямая А),
II турбулентное течение жидкости в гидравлически гладких трубах (прямая В),
III переходная область течения жидкости,.
IV квадратичная область течения жидкости,
3. Понятие «тело давления» и его использование…
Тело давления - объем жидкости, лежащий над криволинейной поверхностью, между вертикальными плоскостями, проходящими через крайние образующие и свободной поверхностью жидкости или ее продолжением.
Возможны два случая расположения криволинейной поверхности под уровнем жидкости. В первом случае жидкость расположена над твердой поверхностью; тело давления заполнено жидкостью и считается положительным, а вертикальная составляющая силы направлена вниз. Во втором случае тело давления не заполнено жидкостью и считается отрицательным; вертикальная сила давления направлена вверх.
Если криволинейная поверхность S замкнута и полностью погружена под уровень абсолютно покоящейся жидкости, то воздействие жидкости сводится к одной вертикальной силе. Действительно, для любой горизонтальной оси существуют две противоположно направленные и равные по величине силы, действующие на тело; поэтому результирующая горизонтальных сил равна нулю. Чтобы найти вертикальную силу, проектируем S на свободную поверхность жидкости. Проектирующие вертикали отметят на поверхности тела замкнутую линию l, которая делит поверхность на две части 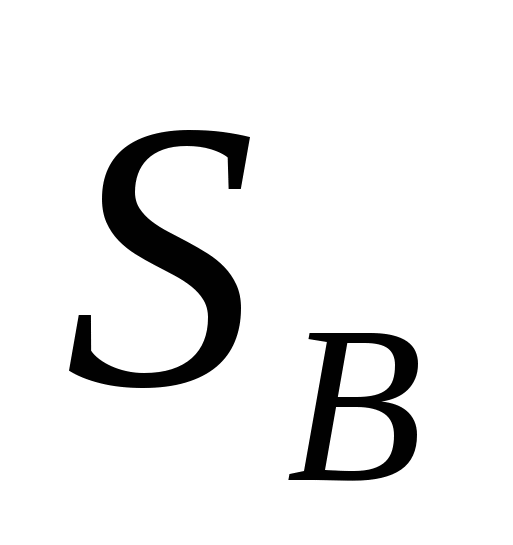 и и 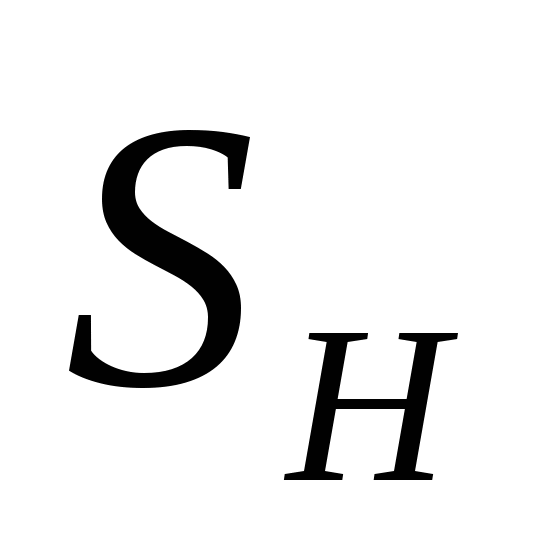 . Для верхней части . Для верхней части 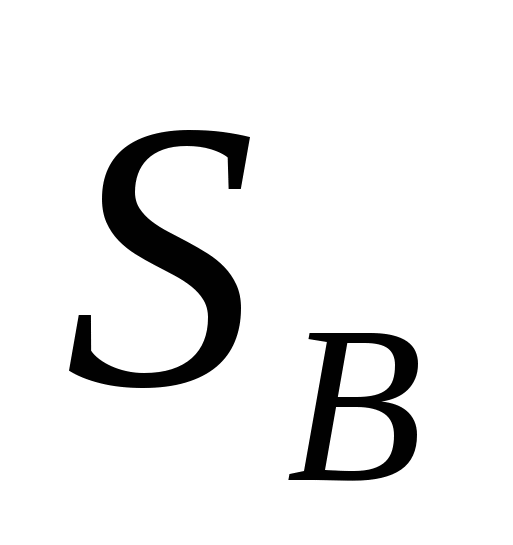 тело давления положительно и соответствующая ему сила направлена вертикально вниз, а для нижней тело давления положительно и соответствующая ему сила направлена вертикально вниз, а для нижней 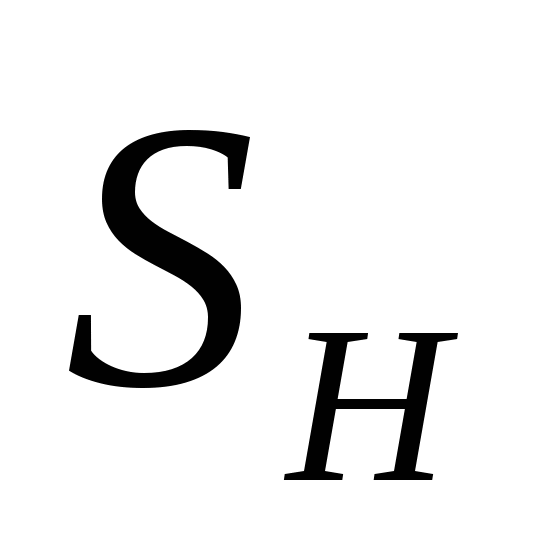 – тело давления отрицательно и сила направлена вверх. Обозначив объемы этих тел давления соответственно через – тело давления отрицательно и сила направлена вверх. Обозначив объемы этих тел давления соответственно через 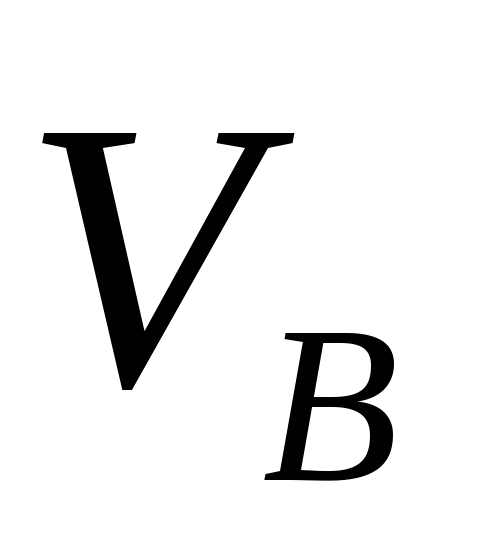 и и 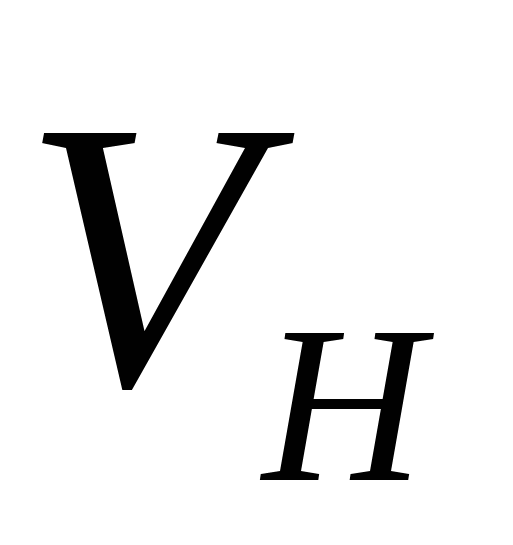 , найдем величину результирующей вертикальной силы А: , найдем величину результирующей вертикальной силы А:
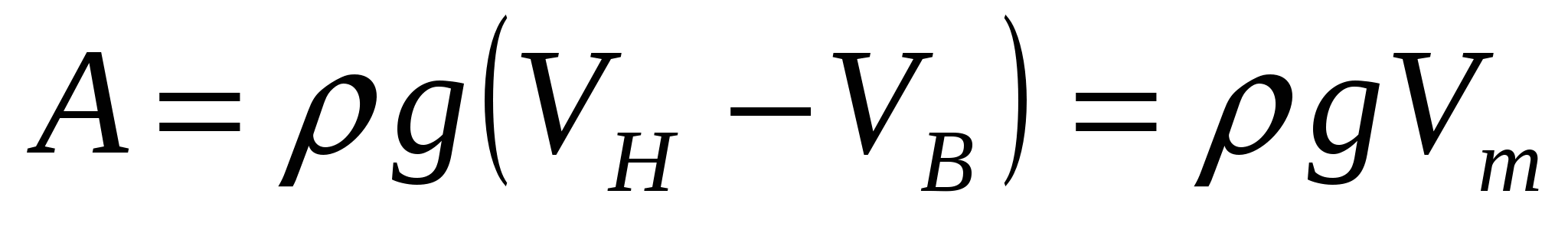 , ,
где 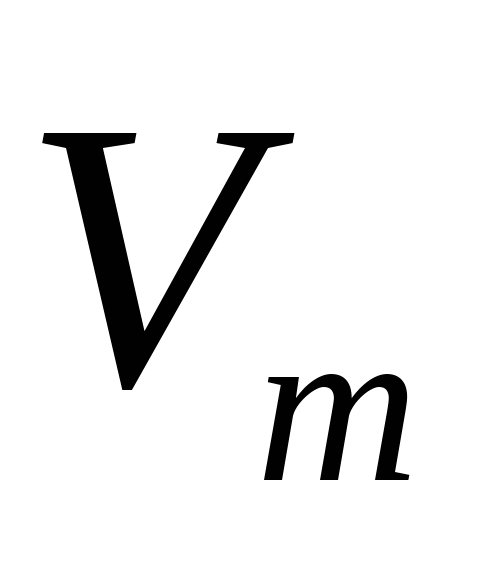 – объем тела. – объем тела. |
 Скачать 0.89 Mb.
Скачать 0.89 Mb.