Шпоры по гидравлике. Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется

• Название: Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется
• Дата: 27.02.2019
• Размер: 0.89 Mb.
• Имя файла: Шпоры по гидравлике.doc
• Тип: Документы; #69072
• страница: 5 из 7

3. Уравнение обращения воздействий для чисто геометрического воздействия: связь между скоростью и площадью поперечного сечения.

В частном случае для геометрического воздействия закон записывается виде уравнения Гогонио:



В случае геометрического воздействия ускорение газового потока требует наличия соответствующего перепада давлений между сечениями входа и выхода из канала. Канал называется идеальным, если течении в нем проходит без трения. Канал, в котором скорость течения увеличивается, называется конфузором (соплом), а в котором уменьшается диффузором.

С сужением дозвуковой поток разгоняется при этом максимальная скорость достигается в выходном сечении канала и в пределе может быть равна местной скорости звука, т.е. критической.
Билет 15.

1. Газодинамические формы уравнения расхода (без вывода). Характер изменения входящих в выражение газодинамических функций.

Q=WF

Газодинамическая функция q(λ)- приведенный расход: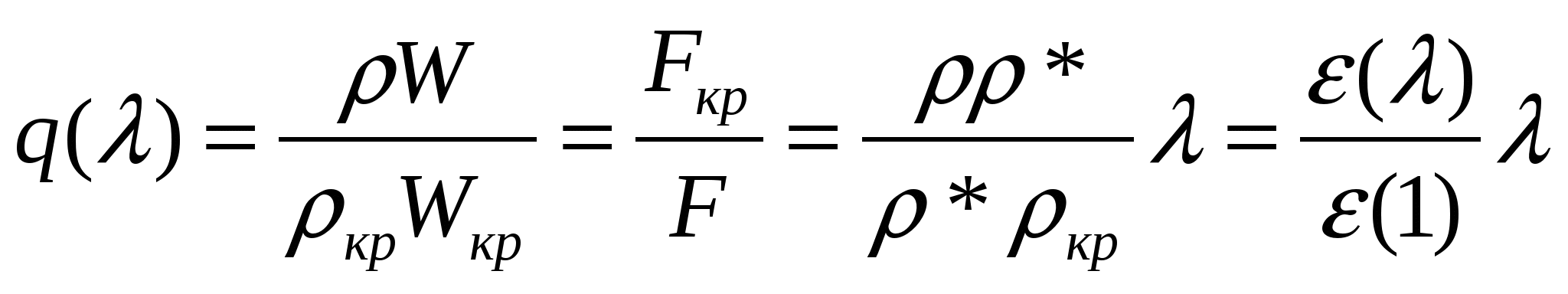





Уравнение расхода в газодинамической форме: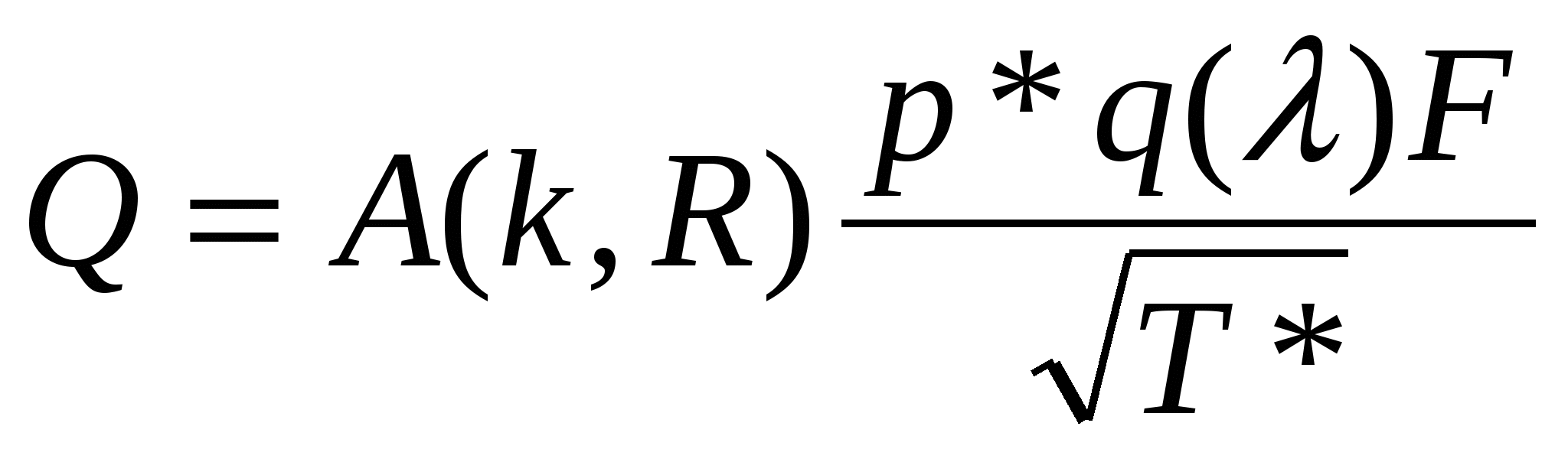

Газодинамическая функция y(λ):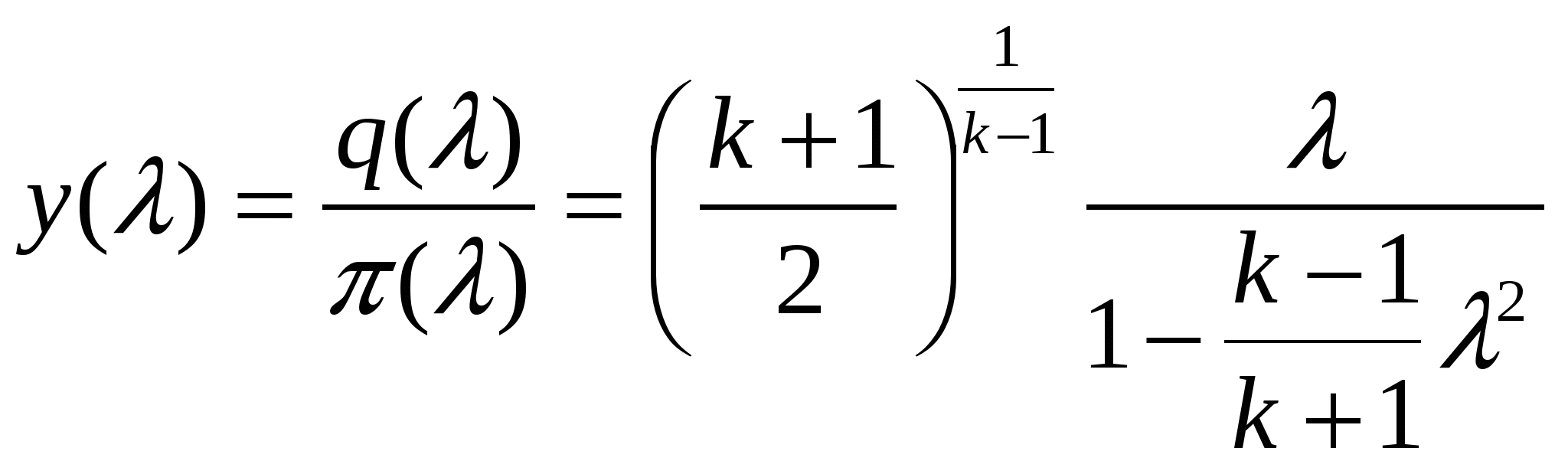

Уравнение расхода в газодинамической форме: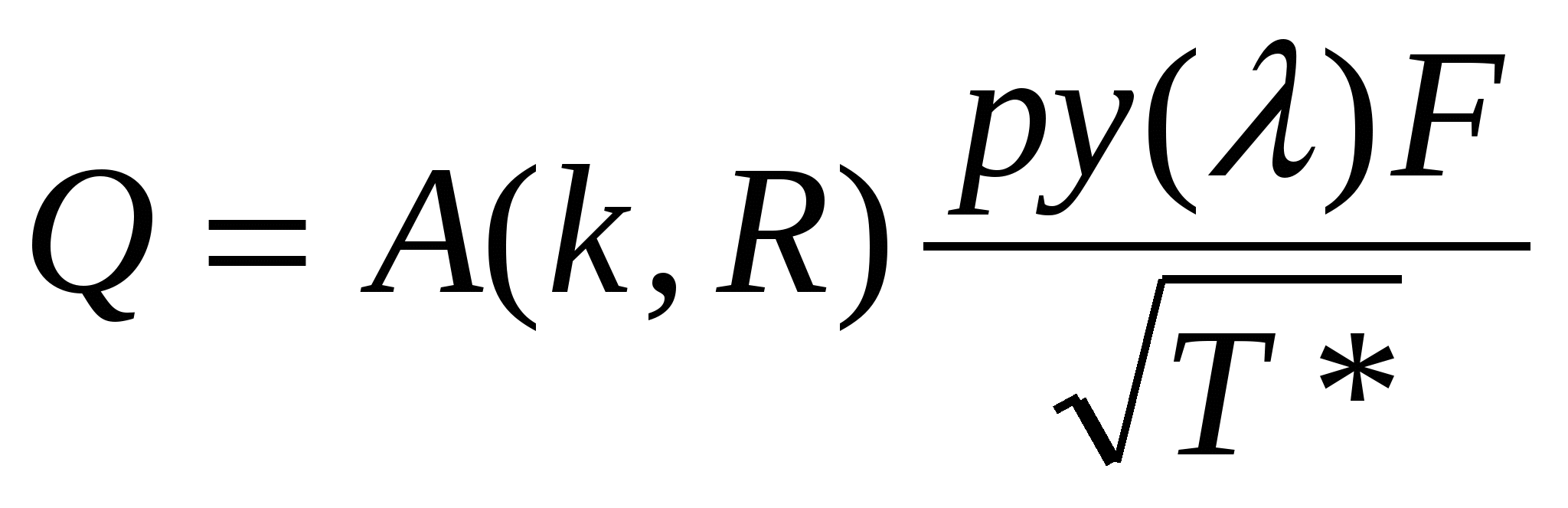

2. Простой трубопровод.

Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением: простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качест­ва его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений.

При напорном движении жидкости простой трубопровод работает полным сечением S=4πR²= const. Размер сечения трубопровода (диаметр или ве­личина гидравлического радиуса), а так­же его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками тру­бопровода являются расход жидкости в трубопроводе Qи напор(на головных сооруже­ниях трубопровода, т.е. в его начале). Большинство других характеристик простого тру­бопровода являются, не смотря на их важность, производными характеристиками. По­скольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна v=const. Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези: v=C√Ri_, где: - скоростной коэффициент Шези, R_г= S/П - гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью R_г=d/4; i=h_тр/l - гидравлический уклон. Полагая, что весь имеющийся напор на головных сооружениях (в начале) трубопро­вода тратится на преодоление сил трения в трубопроводе (в простом трубопроводе это по­тери напора по длине), уравнение движения жидкости (Бернулли) примет вид: H=²l/CR_г.

Расход жидкости в трубопроводе: Q=vS = CS√Ri .

Обозначив: SC√R=K , получим основное уравнение простого трубопровода: Q=K√i.

где: К - модуль расхода - расход жидкости в русле заданного сечения при гид­равлическом уклоне равном единице (иначе модуль расхода называют расходной характе­ристикой трубопровода). Другой и более известный вид основного уравнения простого трубопровода получим, решив уравнение относительно напора: H=Q²/K² или H=RQ²

Величину 1/K² называют удельным сопротивле­нием трубопровода, R=1/Q²- - его полным сопротив­лением

График уравнения простого трубопровода носит название его гидравлической харак­теристики. Вид гидравлической характеристики зави­сит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).

Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквива­лентной длины l_экв: l_экв = l +d∑ξ /λ.
Билет 18.

1. Вязкость и ее проявления при течении реальной жидкости. Гипотеза Ньютона.

Вязкостью наз. свойство всех реальных жидкостей оказывать сопротивление относительному сдвигу частиц, т.е. изменению их формы.

Опыт показывает, что скорость жидкости у нижней пластины равна нулю, у верхней –u, а скорость между пластинами распределена линейно, давление во всей области постоянно. Такое течение называют течением чистого сдвига.

Ньютон экспериментально установил закон о молекулярном трении в жидкости: напряжение трения пропорционально поперечному градиенту скорости:

, где  - вязкости или касательные напряжения;  - коэффициент пропорциональности. Величина  зависит от природы жидкости, его агрегатного состояния, температуры и не зависит от давления. Кинематическая вязкость = /.

3. Уравнение движения идеальной жидкости в форме Эйлера.

В потоке идеальной жидкости возьмем произвольную точку М с координатами x, y, z и выделим у этой точки элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка М была бы одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны x, y и z. Составим уравнение движения выделенного элемента жидкости массой xyz. Так же, как и при рассмотрении равновесия подобного объема жидкости будем считать, что внутри этого объема на жидкость действует результирующая массовая сила, составляющая которой, отнесенные к единице массы, равны X, Y, и Z. Тогда массовые силы, действующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема. Если давление в точке М обозначить через p, разность сил давлений, действующих на параллелепипеде, составляет .Скорость движения жидкости в точке М обозначим через v, а ее компоненты – через v_x (xyz). Тогда проекции ускорения, с которым движется выделенный объем, будут равны: dv_x/dt (xyz). Уравнения движения выделенного объема жидкости в проекциях на координатные оси будут иметь вид: xyz dv_x/dt=Xxyz-. (XYZ).

Разделим эти уравнения почленно на массу элемента и перейдем к пределу, устремляя одновременно x, y и z к нулю, т.е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения движения жидкости, отнесенные к точке М: dv_x/dt=X -. (XYZ). Полученная система дифференциальных уравнений движения идеальной жидкости носит название уравнений Эйлера. Смысл6 полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления
Билет 19.

1. Свойства давления.

Жидкости и газы в силу своего строения не могут воспринимать растягивающие напряжения. Поэтому нормальные напряжения должны быть сжимающими. Такое сжимающее нормальное напряжение называется давлением и обозначается p: p =-p_n= -_x= -_y= -_z. (1)

Сле-но, давление всегда направлено по внутренней нормали к поверхности жидкости. Это первое свойство давления.

Перепишем (1) p =p_x= p_y= p_z, где p_x= -_x, p_y= -_y, p_z= -_z. Давление – величина положительная и в любой точке идеальной или покоящейся вязкой жидкости одинаковая по всем направлениям, т.е. не зависит от ориентации площадки в пространстве. Это второе свойство давления. Но давление неодинаково в различных точках пространства и может изменяться во времени.
3. Дроссельные расходомеры: принципы работы и использование.

Назначение дросселей – устанавливать желаемую связь между пропускаемым расходом и перепадом давления до и после дросселя. По характеру рабочего процесса дроссели являются гидравлическими сопротивлениями с регламентированными характеристиками. Применение дросселей в качестве регулирующих элементов требует двух качеств: возможности получения характеристики p=f(Q); сохранение стабильности характеристики при эксплуатации, а именно ее малой зависимости от изменения температуры жидкости, неподверженность засорениям, облитерация.

Пакетные дроссели, составленные из шайб с отверстиями; трубы Вентури, сопло.

С учетом потерь напора формула расхода водомера Вентури запишется так:

, (80)

где – коэффициент расхода водомера, учитывающий потери напора в водомере. Для новых водомеров ; для водомеров, бывших в употреблении, .

Из уравнения Бернулли: , или .

Т.к. , поэтому . (а)

В уравнении (а) две неизвестные величины и . Составим второе уравнение, используя уравнение неразрывности , откуда .

Подставляя в уравнение (а), получим .

Отсюда скорость течения в основной трубе (сечение 1-1) равна ,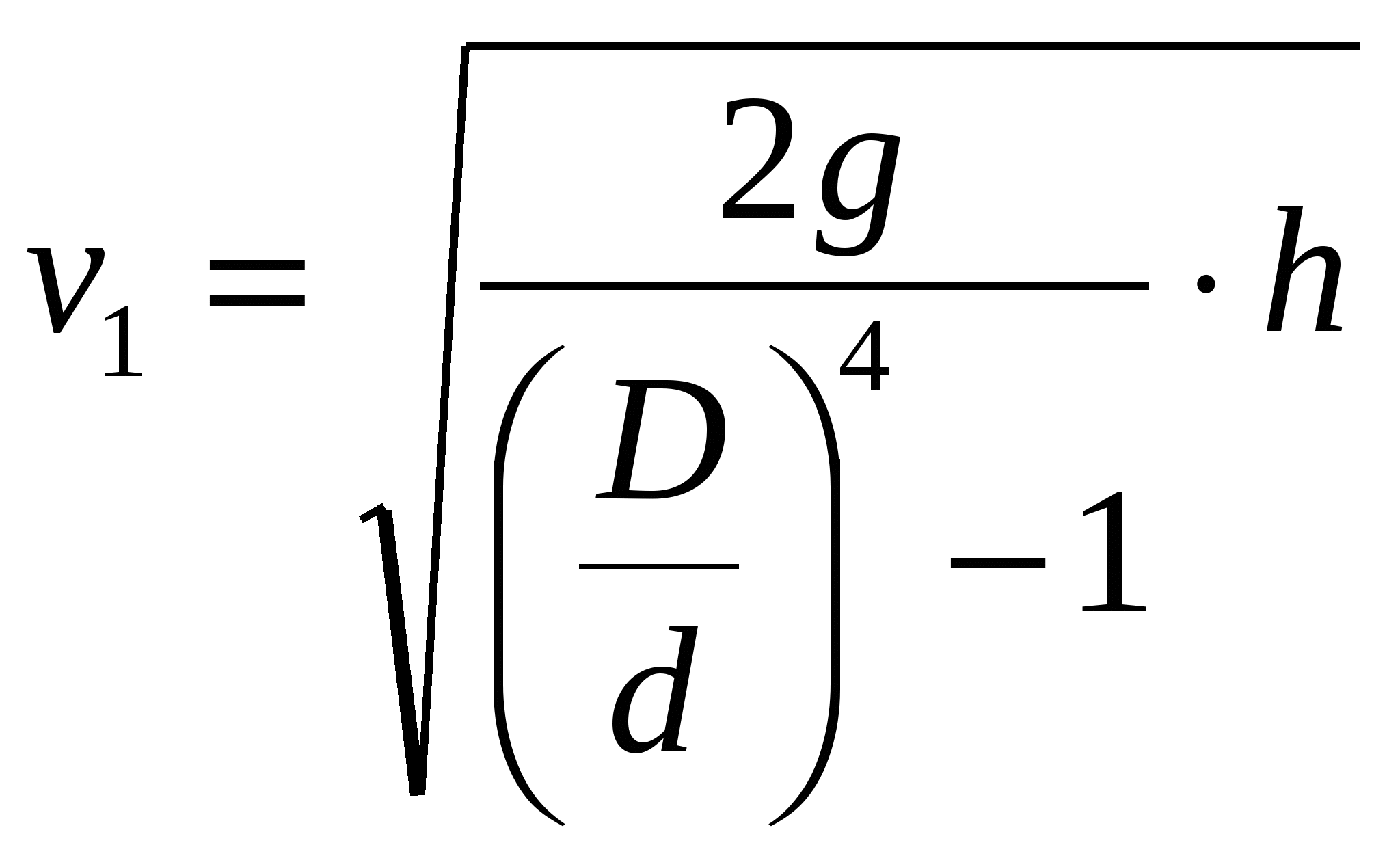

расход жидкости в трубе по формуле: или , где K- постоянная.
Билет 25.

1. Степень (интенсивность) турбулентности. Изотропная турбулентность.

Степенью турбулентности  или интенсивностью турбулентности называется отношение средней пульсационной составляющей к среднемассовой скорости потока. Для неизотропной турбулентности .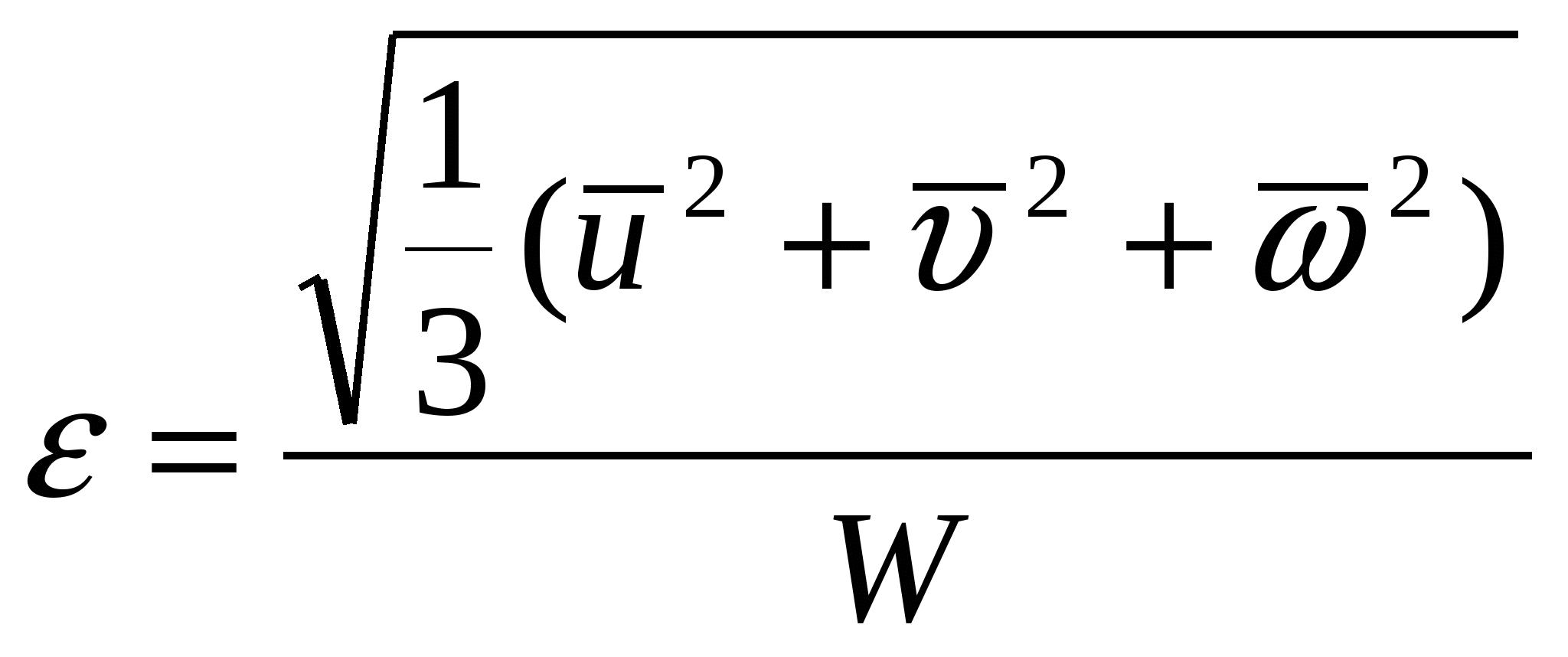
Для изотропной турбулентности: .

Изотропной турбулентностью называется турбулентное течение, в котором средние пульсационные скорости одинаковы во всех направлениях .
2. Вывод критериев подобия на основе теории подобия.

Метод подобия используется в том случае, когда исследуемое физическое явление может быть описано дифференциальными уравнениями. В этом случае числа подобия легко определяются как коэффициенты уравнений, представленных в безразмерном виде.

Если физическое явление не имеет математического описания, определение чисел подобия производится методом анализа размерностей. Степень сложности уравнений при использовании метода подобия не имеет значения, т.к. для нахождения чисел подобия решение уравнений не требуется.

Общим условием гидродинамического подобия процессов является соблюдение геометрического, кинематического и динамического подобия.

При геометрическом подобии связь между геометрическими параметрами объектов должна удовлетворять условию m_l=l_м/l_н, где l-линейный размер, m_l- линейный масштаб моделирования, индексы м-модель, н –натура.

Кинематическое подобие выполняется, если в сходственных точках, координаты которых удовлетворяют соотношением: m_l=x_м/x_н =y_м/y_н =z_м/z_н =l_ом/l_он, проекции векторов скорости удовлетворяют условию: : m_w=u_м/u_н =_м/_н =_м/_н =u_ом/u_он , где l_о - некоторый характерный линейный размер, u_о- некоторое характерное значение скорости, m_w- масштаб скорости.

Сходственные точки модели и натуры имеют одинаковые безразмерные координаты, и в этих точках одинаковые безразмерные значения соответственных составляющих скорости.

Динамическое подобие означает пропорциональность всех сил, действующих в сходственных точках геометрически подобных потоков.

Если физическое явление описывается дифференциальными уравнениями, то эти уравнения окажутся пригодными для описания любого явления, подобного рассматриваемому.

Для примера рассмотрим получение чисел подобия из уравнений Навье - Стокса (случай несжимаемой жидкости, находящейся в изотермических условиях в поле силы тяжести ). Воспользуемся только первым из уравнений: проекцией на ось x

.

Приведем это уравнение к безразмерному виду. Для этого выберем характерные параметры, которым присвоим нижний индекс о и отнесем к ним соответствующие размерные величины. Тогда уравнение Навье - Стокса с развернутыми компонентами представится в виде

Для геометрически подобных потоков условия динамического подобия соблюдаются, если обеспечено равенство безразмерных комплексов:

.

Полученные безразмерные комплекса являются числами подобия: -число Фруда; -число Эйлера; -число Рейнольдса; число Струхоля.
3. Принцип экспериментального определения гидравлических потерь на трение.

Экспериментально подтверждается, что при турбулентном режиме движении потери напора по длине зависят от состояния стенок, ограничивающих поток. Если пропускать по трубе жидкость с различными скоростями, начиная с ламинарного режима и постепенно переходя к турбулентному, и одновременно измерять потери напора, то можно получить график зависимости потерь напора от скорости (рис.). График показывает, что при скорости меньше некоторого предела потери напора прямо пропорциональны первой степени скорости (на графике участок 0-1). Как и следовало ожидать, этот предел соответствует критической скорости (1)

После перехода от ламинарного режима к турбулентному потери напора растут пропорционально скорости в степени, большей единицы (на графике участок кривой 2-3). Переход от ламинарного режима к турбулентному может происходит и при числах Рейнольдса, больших критического.

Обратный же переход от турбулентного режима к ламинарному осуществляется при почти одинаковом значении , которое и считается критическим.

Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению ,

где l – длина участка трубы, м; d–внутренний диаметр трубопровода, м; v – средняя скорость потока, м/сек; g–ускорение свободного падения, м/сек²; – безразмерный коэффициент гидравлического трения.

Впервые формула (2) была получена эмпирическим путем в XIX в. и названа формулой Дарси-Вейсбаха. В дальнейшем указанная формула проверена теоретически на основе метода анализа размерностей.
Билет 31.

1. Общие условия гидрогазодинамического подобия.

Метод подобия используется в том случае, когда исследуемое физическое явление может быть описано дифференциальными уравнениями. В этом случае числа подобия легко определяются как коэффициенты уравнений, представленных в безразмерном виде.

Если физическое явление не имеет математического описания, определение чисел подобия производится методом анализа размерностей. Степень сложности уравнений при использовании метода подобия не имеет значения, т.к. для нахождения чисел подобия решение уравнений не требуется.

Общим условием гидродинамического подобия процессов является соблюдение геометрического, кинематического и динамического подобия.

При геометрическом подобии связь между геометрическими параметрами объектов должна удовлетворять условию m_l=l_м/l_н, где l-линейный размер, m_l- линейный масштаб моделирования, индексы м-модель, н –натура.

Кинематическое подобие выполняется, если в сходственных точках, координаты которых удовлетворяют соотношением: m_l=x_м/x_н =y_м/y_н =z_м/z_н =l_ом/l_он, проекции векторов скорости удовлетворяют условию: : m_w=u_м/u_н =_м/_н =_м/_н =u_ом/u_он , где l_о - некоторый характерный линейный размер, u_о- некоторое характерное значение скорости, m_w- масштаб скорости.

Сходственные точки модели и натуры имеют одинаковые безразмерные координаты, и в этих точках одинаковые безразмерные значения соответственных составляющих скорости.

Динамическое подобие означает пропорциональность всех сил, действующих в сходственных точках геометрически подобных потоков.

Например, для массовых сил: m_R=X_м/X_н= Y_м/Y_н = Z_м/Z_н, где m_R –масштаб сил.