3. Формы уравнения энергии и их физический смысл.
Закон сохранения энергии в применении к энергетически неизолированному жидкому объему V, находящемуся в движении, можно сформулировать так: изменение полной энергии выделенного объема за единицу времени равно сумме работ массовых и поверхностных внешних сил, приложенных к объему и ограничивающей его поверхности, плюс тепло, подведенное извне за то же время.
Дифференциальная форма уравнения энергии для движущейся вязкой сжимаемой жидкости в виде:
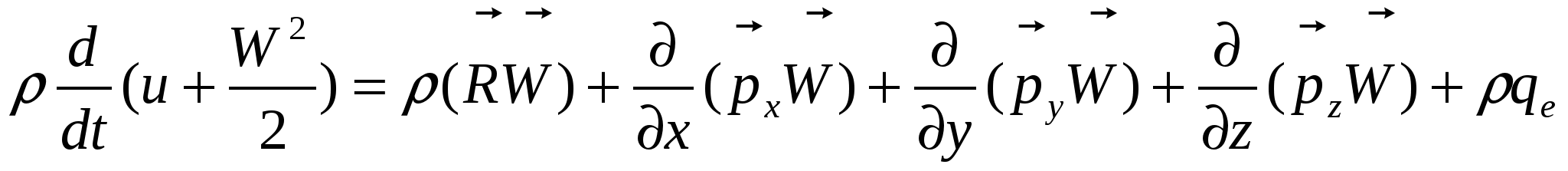 ,где qe –количество тепла, подводимое извне к единице массы жидкости в единицу времени. Внешний теплоподвод может осуществляться теплопроводностью, конвекцией, излучением. Внешним считается приток тепла за счет фазовых и химических превращений, происходящих в самой жидкости. ,где qe –количество тепла, подводимое извне к единице массы жидкости в единицу времени. Внешний теплоподвод может осуществляться теплопроводностью, конвекцией, излучением. Внешним считается приток тепла за счет фазовых и химических превращений, происходящих в самой жидкости.
Уравнение энергии в форме энтальпии:
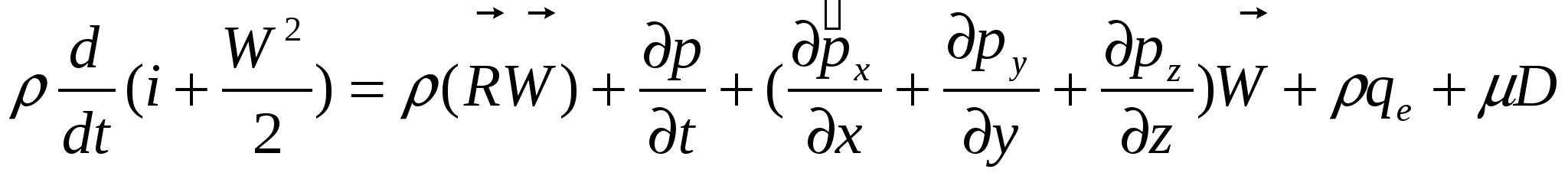
Рассмотрим адиабатическое течение, при котором отсутствует приток внешнего тепла и теплообмен между частицами жидкости, т.е. Qe=0. Будем считать, что жидкость идеальная (=0), течение установившееся, а массовые силы имеют потенциал. Тогда из уравнения энергии получим:  . .
Билет 9.
1. Постой и сложный трубопровод.
Простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качества его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений. Основное уравнение простого трубопровода: Q=K√i. При напорном движении жидкости простой трубопровод работает полным сечением S=4πR²= const. Размер сечения трубопровода (диаметр или величина гидравлического радиуса), а также его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками трубопровода являются расход жидкости в трубопроводе Qи напор (на головных сооружениях трубопровода, т.е. в его начале)
К сложным трубопроводам следует относить те трубопроводы, которые не подходят к категории простых трубопроводов, т.е. к сложным трубопроводам следует отнести:
трубопроводы, собранные из труб разного диаметра (последовательное соединение трубопроводов),
трубопроводы, имеющие разветвления: параллельное соединение трубопроводов, сети трубопроводов, трубопроводы с непрерывной раздачей жидкости.
Потери напора в трубопроводе, состоящем из последовательно соединённых друг с другом участков равны квадрату расхода жидкости в трубопроводе умноженному на сумму удельных сопротивлений всех участков.
Схема прокладки параллельных трубопроводов используется в тех случаях, когда на трассе магистрального трубопровода есть участки, где требуется уменьшить гидравлические сопротивления трубопровода (высокие перевальные точки трубопровода) или при заложении трубопровода в трудно доступных местах (переход через реки и др.).
2. Связь изменения энтропии с изменением параметров торможения газового потока.
Для неизолированных систем, участвующих во взаимодействии с внешней средой, уравнение 2 з-на термодинамики определяет изменение энтропии совершенного газа в процессе 1-2 по значению параметров состояния 2-1 в виде: 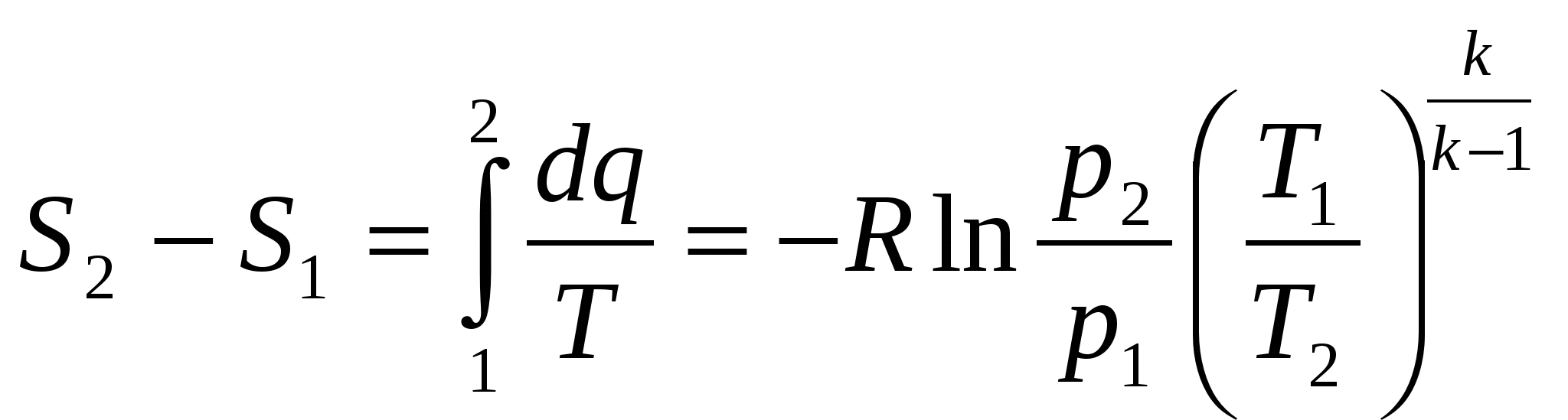
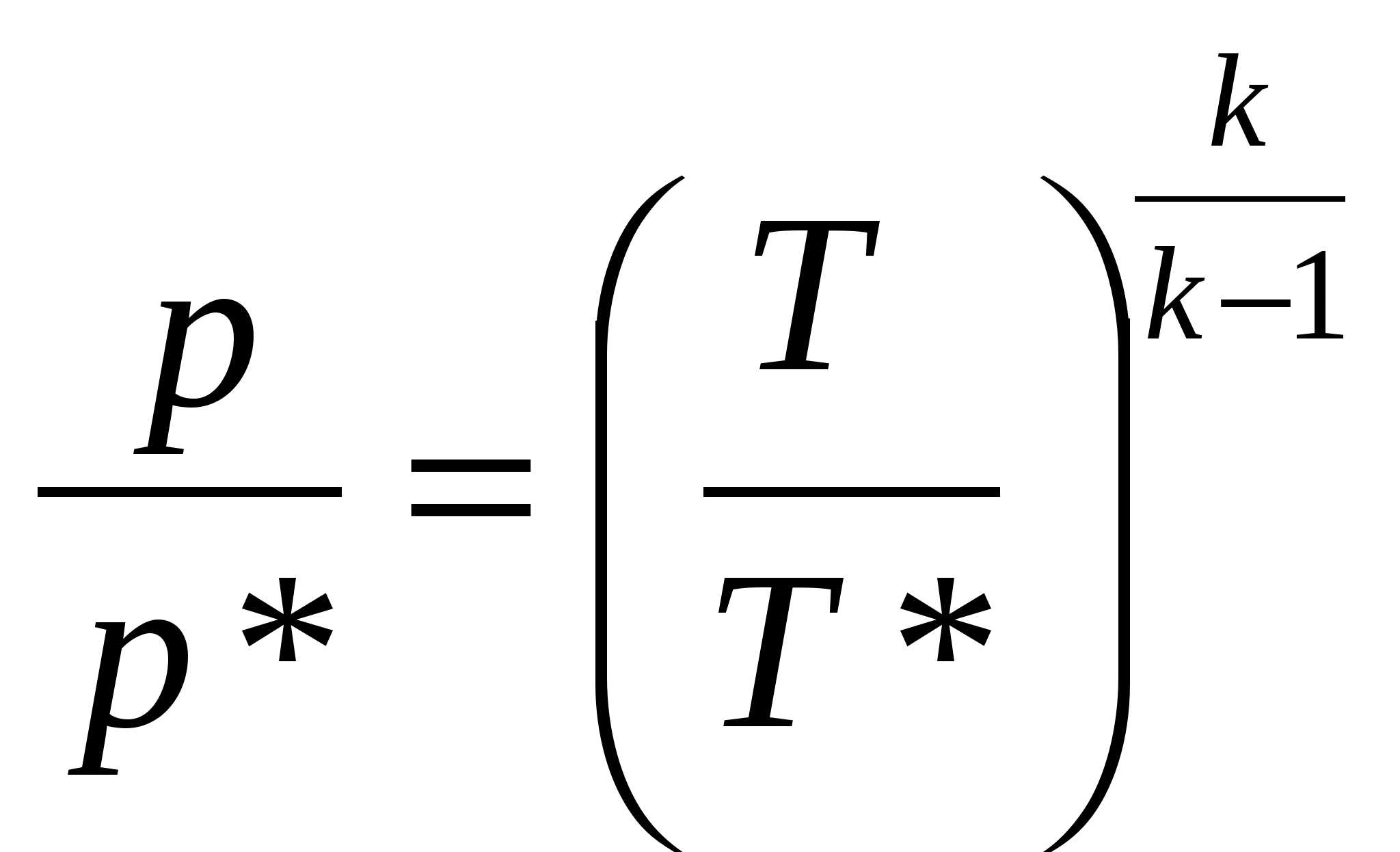 ; ; 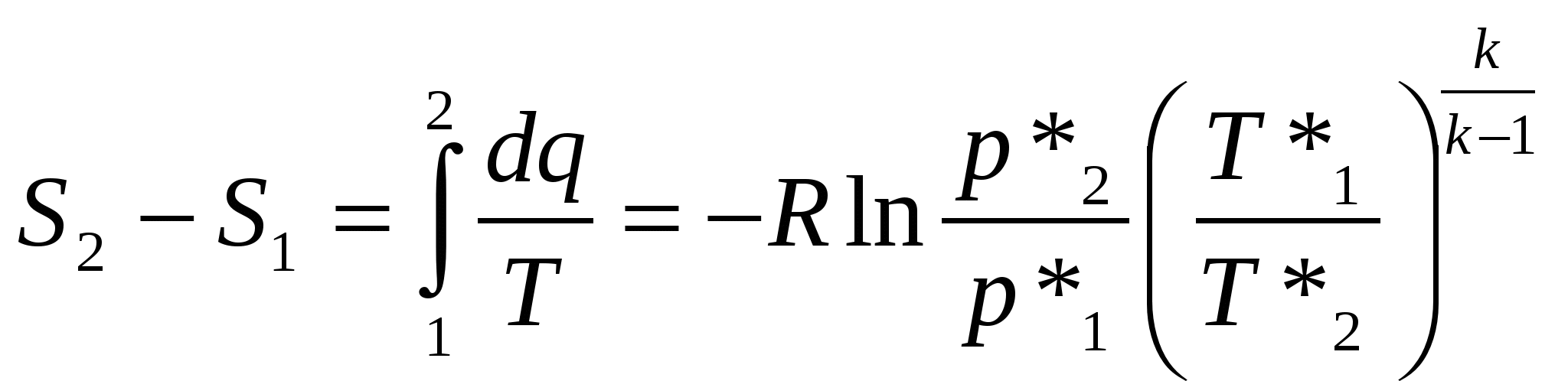
dq=dqe+dqz
1.dq=0 → S2-S1 =0 или S2-S1 =const, т.е. рассматриваемый процесс изоэнтропический, при этом dqe =0 - процесс адиабатический и dqz =0 - нет трения, но техническая работа не равна 0. Согласно уравнению 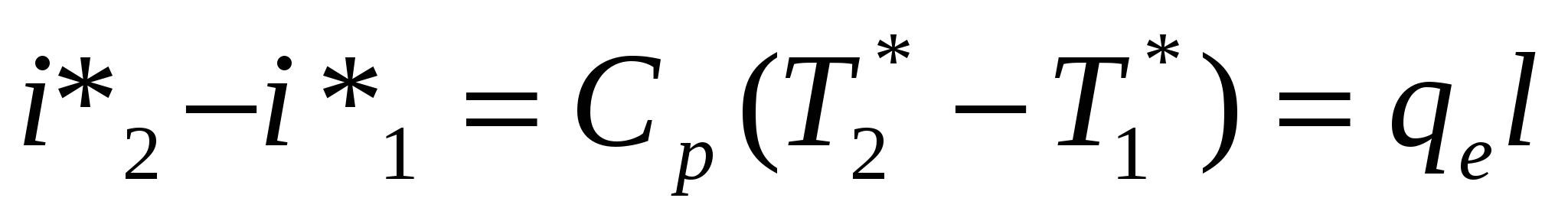 при dqe =0, получим при dqe =0, получим 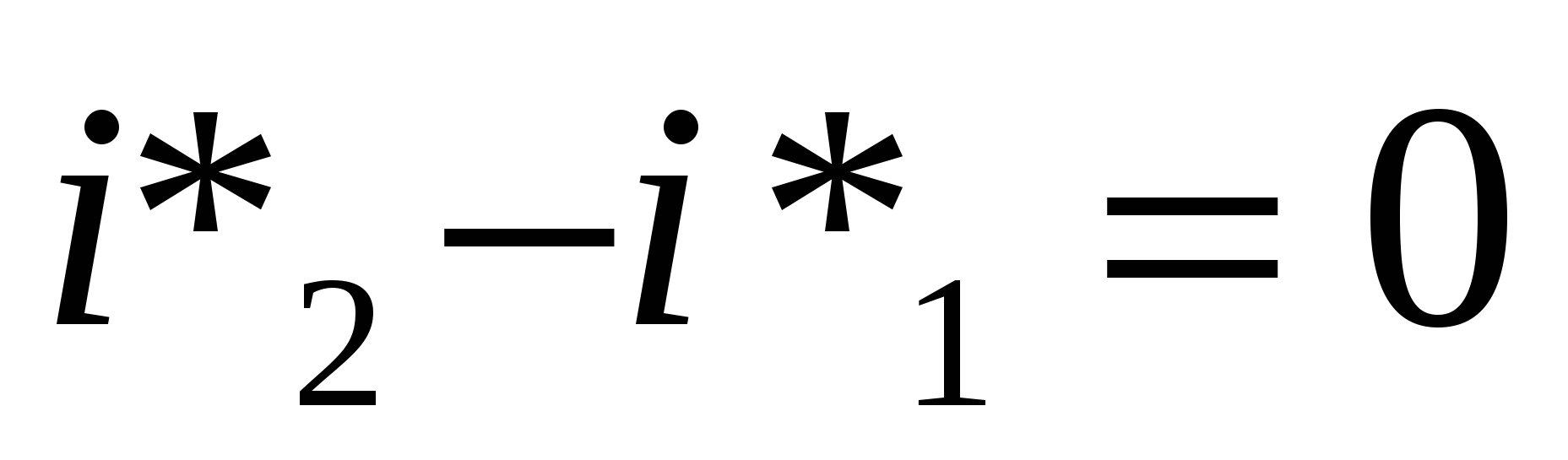 . .
Под действиемм технической работы над газом меняется полная энтальпия .
2. {1} + l=0, т.е процесс идеальный энергоизолированный. 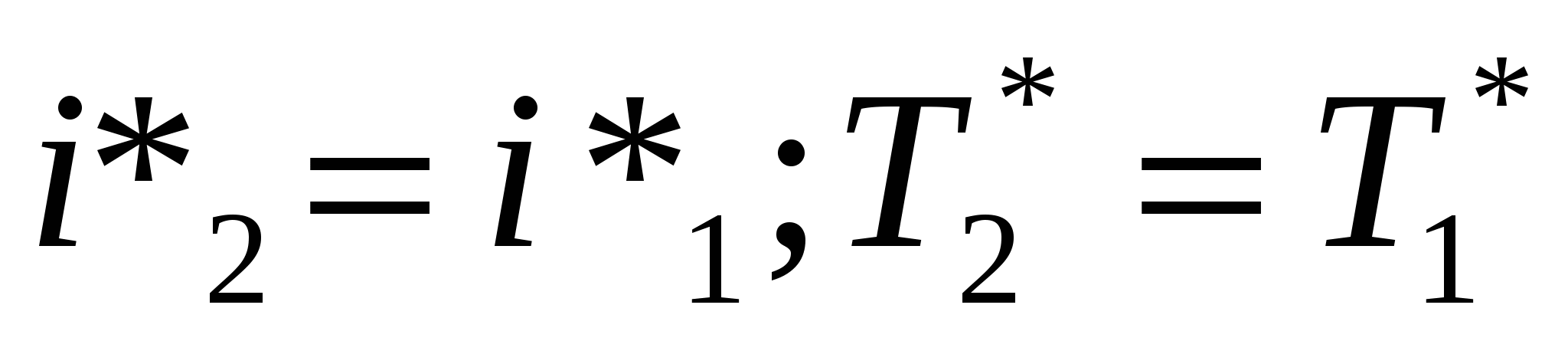 → p*1=p*2. → p*1=p*2.
Следовательно, в идеальном энергоизолированном процессе давление торможение сохраняется постоянным. Поэтому за параметры заторможенного потока и прменяют параметры такого торможения (без потерь).
3. Если течение энергоизолированно, но не идеальное: qe=0, С=0, то 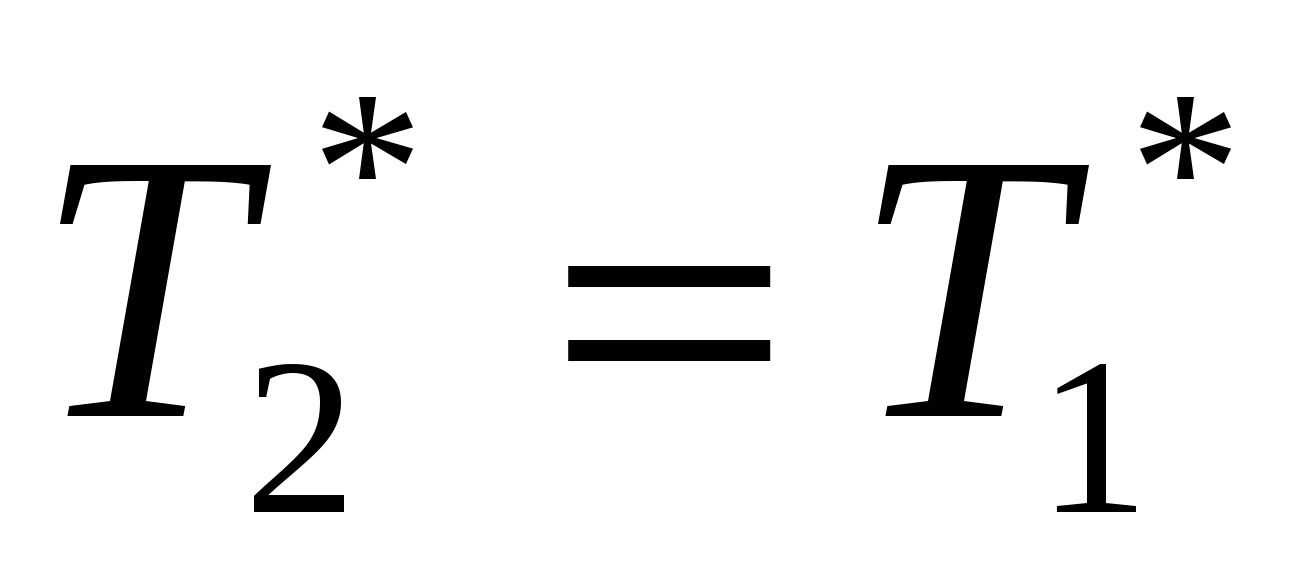
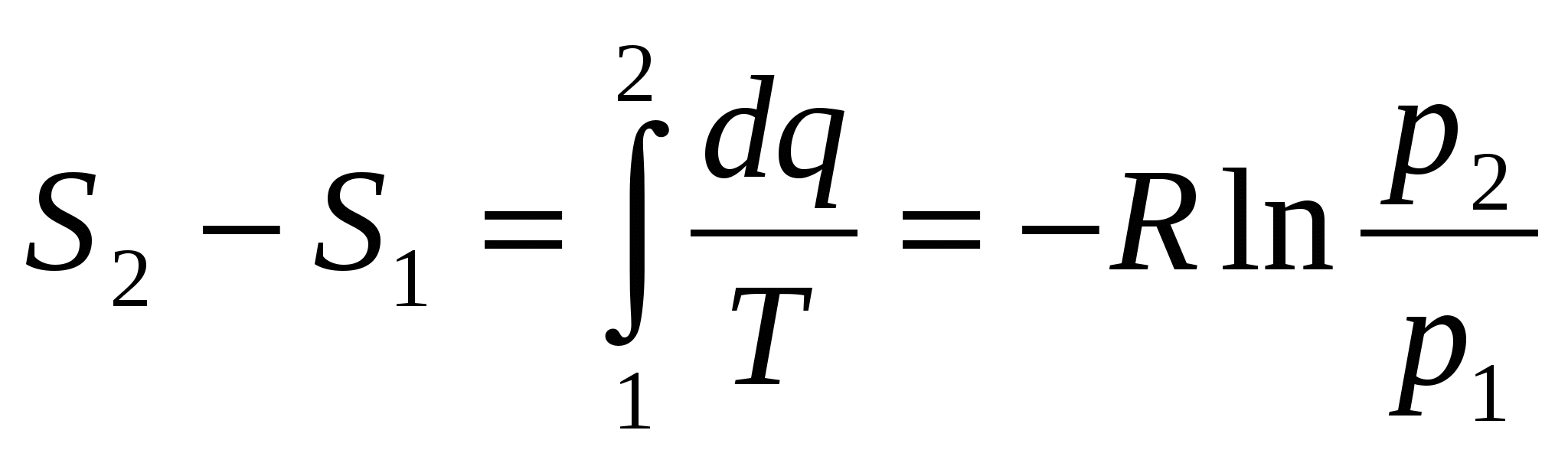
Т.к. теплота трения положительна, то S2-S1 >0, то 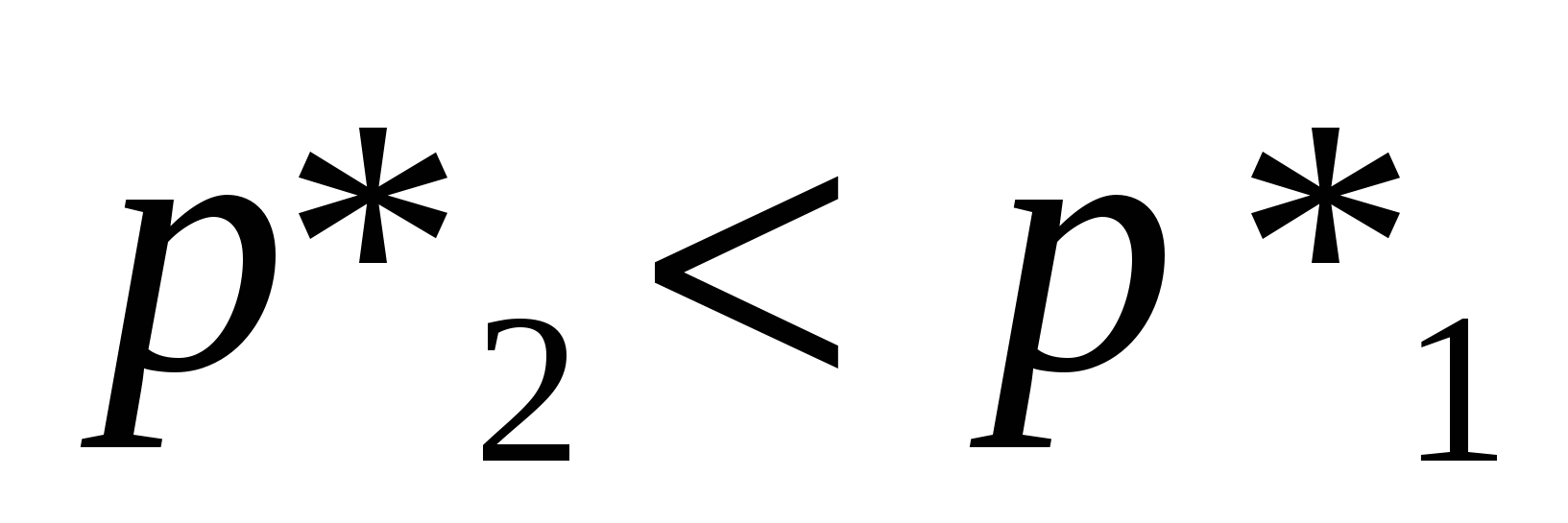 . .
Т.е. под воздействием трения и других гидравлических сопротивлений полное давление падает.
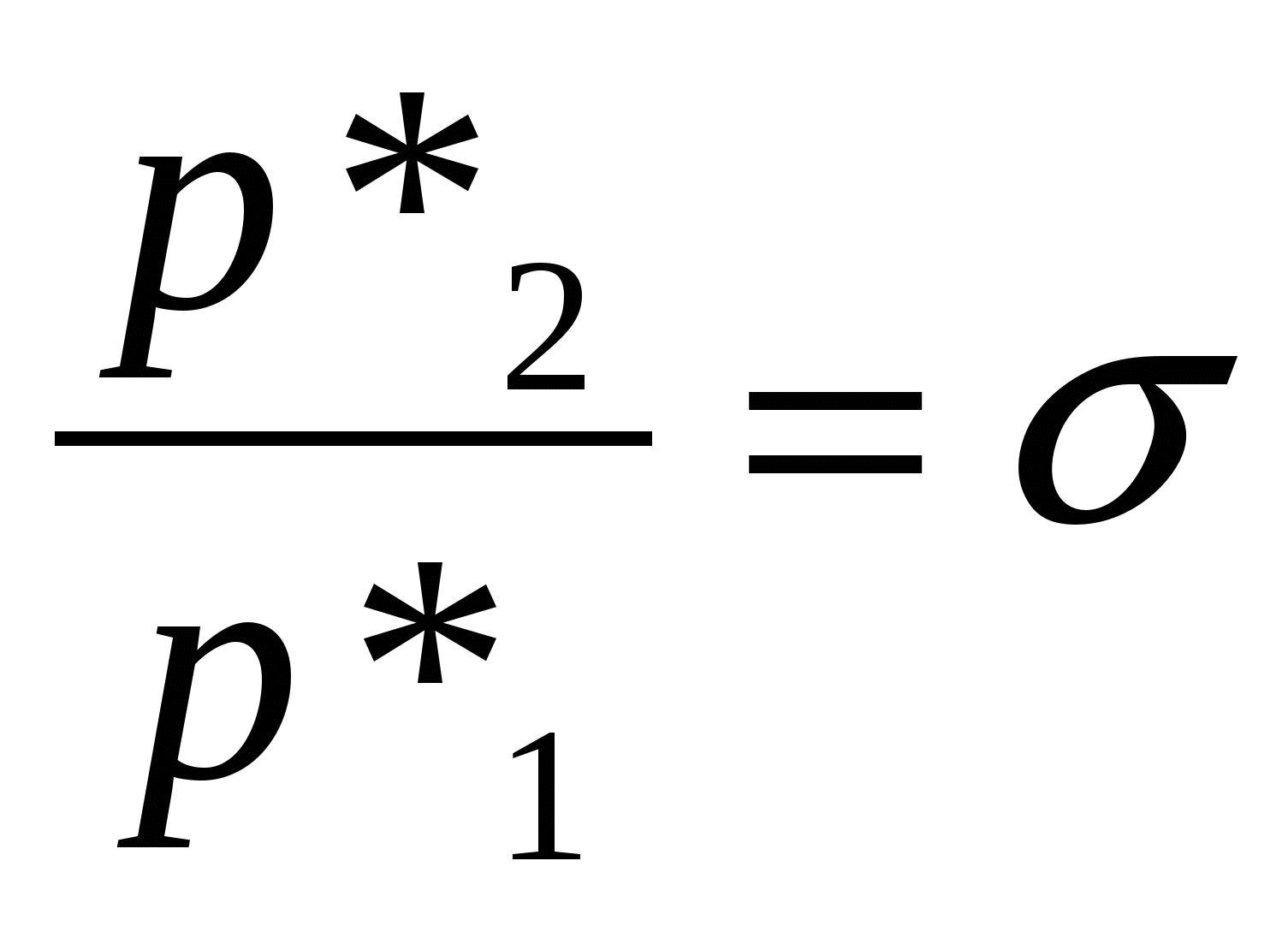 , где σ – коэффициент полного давления. , где σ – коэффициент полного давления.
Изменение давления торможения зависит только от изменения энтропии и температуры торможения на рассматриваемом участке элементарной струйки. Увеличение энтропии всегда способствует уменьшению давления торможения, а увеличение температур торможения – его увеличению.
3. Уравнение обращения воздействия как общий случай одномерного течения газа (основные свойства и значения уравнения для анализа течения газа).
Уравнение обращения воздействия:
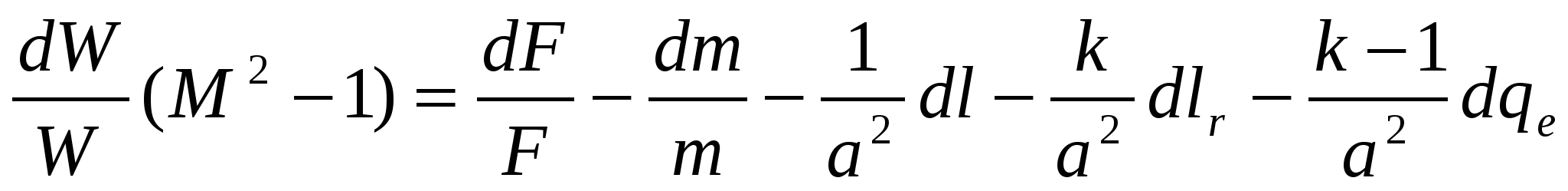 , ,
где dF- геометрическое воздействие; dm-расходное воздействие;
dqе – термодинамическое воздействие; dl-динамическое воздействие;
dlr – работа трения.
Знак в левой части уравнения меняется при переходе M через 1, следовательно влияние отдельных физических воздействий, или комбинаций воздействий на течение газа противоположны для дозвукового и сверхзвукового течения. Для непрерывного изменения скорости газа в одну сторону за чет одного физического воздействия необходима, чтобы знак воздействия менялся на обратный в момент перехода через скорость звука, т.е. в момент возникновения критического течения. Это возможно для всех воздействий кроме воздействия трения. Т.о. при воздействии трения переход через скорость звука невозможно.
Если в процессе участвуют одновременно несколько воздействий, то для непрерывного изменения скорости в момент времени перехода через скорость звука должен смениться на обратный знак их суммы
Билет 16.
1. Газодинамические формы выражения для полного импульса потока в сечении. Характер изменения входящих в формулы газодинамических функций.
Полный импульс можно выразить:
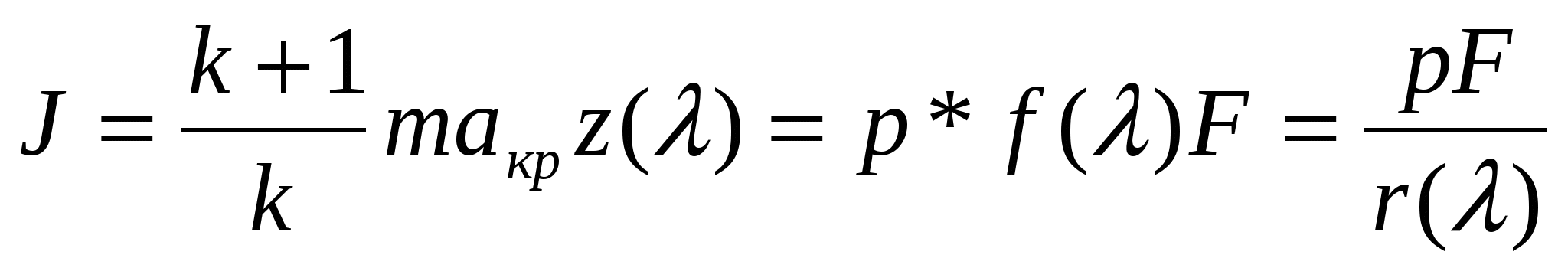 . .
Газодинамическая функция z(λ) =J/Jкр = λ+1/λ зависит только от λ и не зависит от k, принимает минимальное значение 1 при λ=1.
Функция f(λ) равна отношению полного импульса к полному импульсу газа, заторможенного в том же сечении.
Функция r(λ) равна отношению статистической составляющей полного импульса к полному импульсу.
f(λ)= λ(λ)z(λ) и r(λ)=(λ)/f(λ)
2. Потери при внезапном расширении трубы.
Внезапное расширение потока (рис. 1. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора.
Р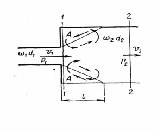 ассмотрим внезапное расширение трубы с горизонтальной осью. Потеря напора на внезапное расширение равна ассмотрим внезапное расширение трубы с горизонтальной осью. Потеря напора на внезапное расширение равна
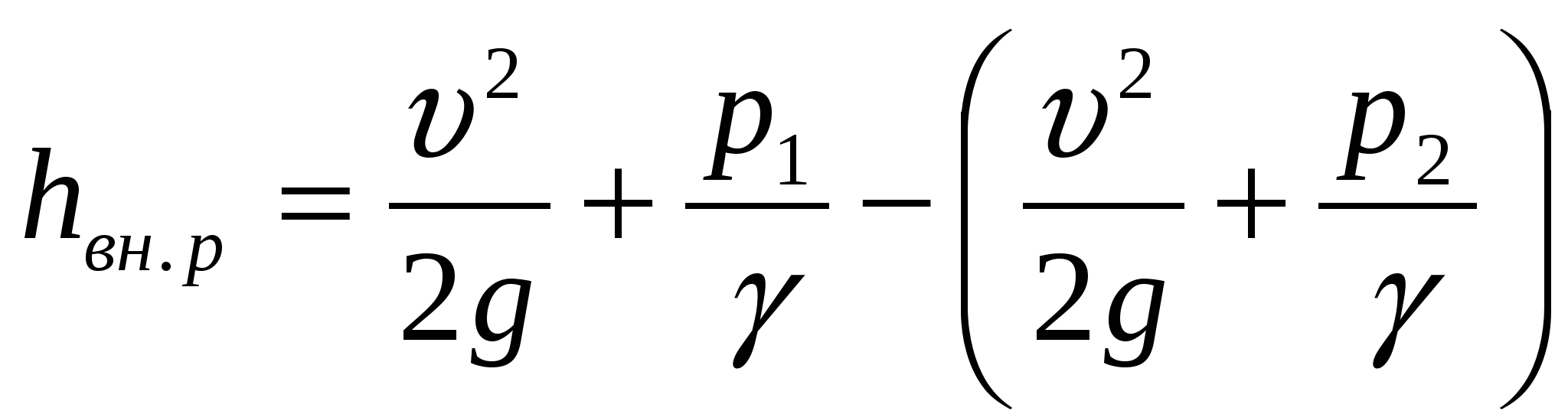 . (103) . (103)
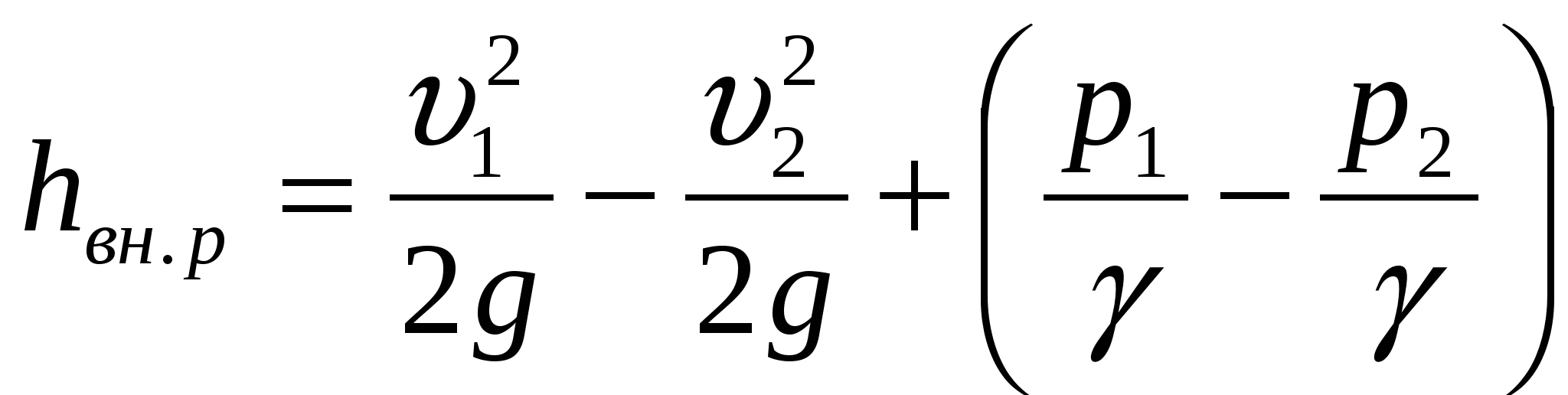
Разность давлений 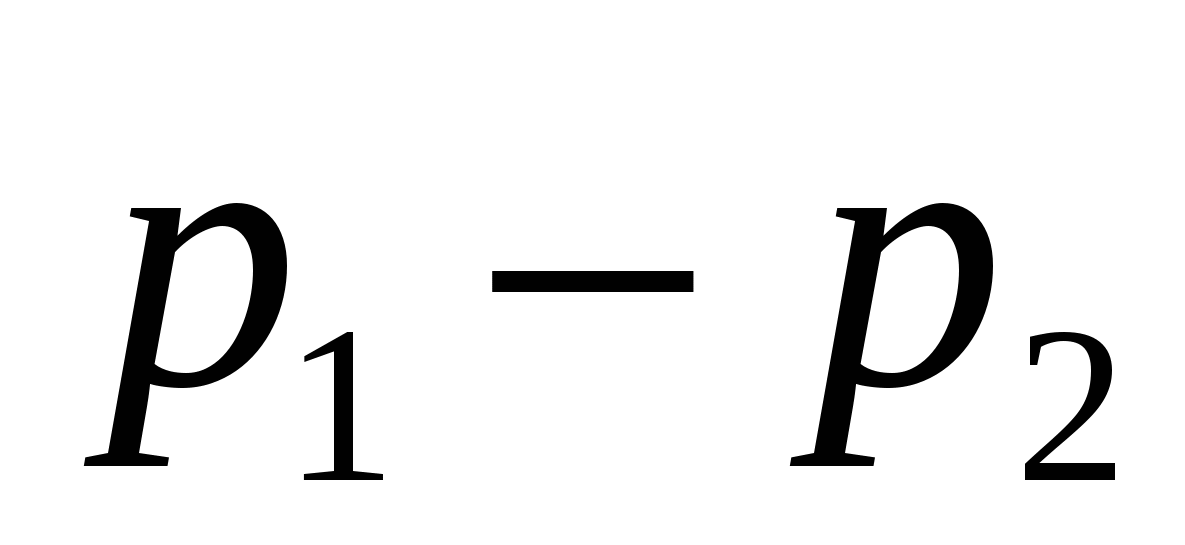 найдем, применив уравнение количества движения к отсеку жидкости между сечениями 1-1 и 2-2. За время tчерез сечения 1-1 и 2-2 протечет масса жидкости найдем, применив уравнение количества движения к отсеку жидкости между сечениями 1-1 и 2-2. За время tчерез сечения 1-1 и 2-2 протечет масса жидкости 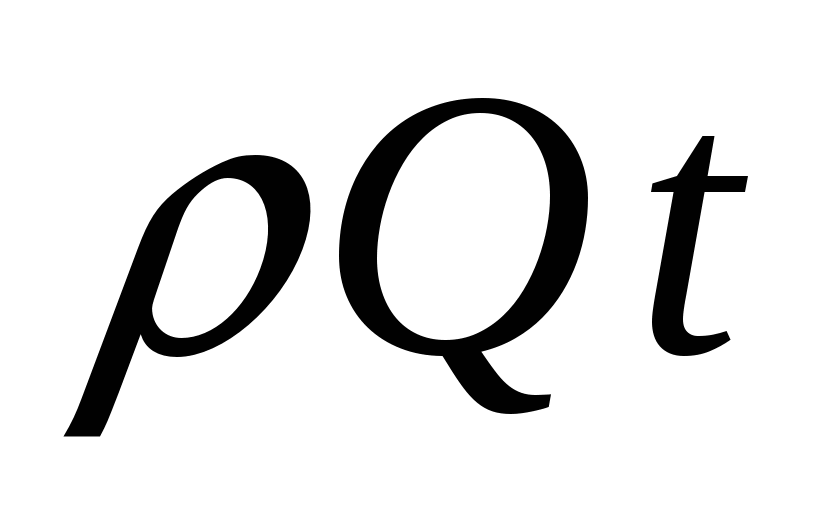 , количество движения которой в сечении 1-1, где скорость , количество движения которой в сечении 1-1, где скорость 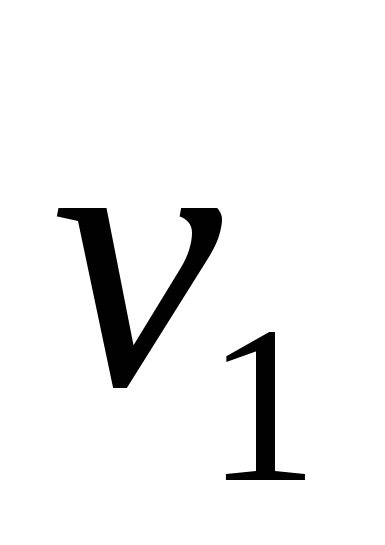 равно равно 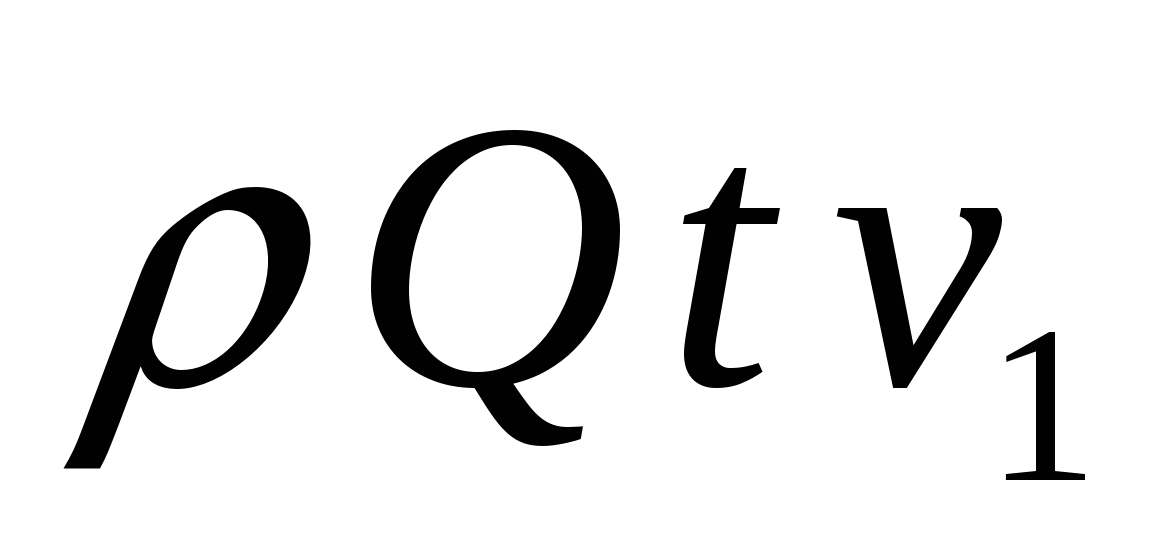 , а в сечении 2-2 – , а в сечении 2-2 – 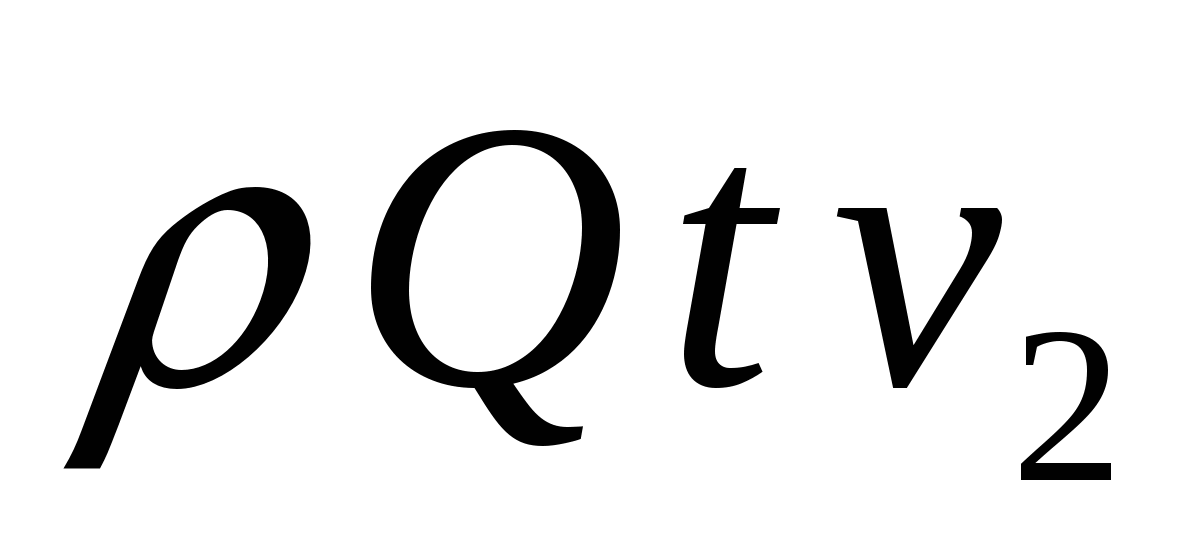 , т. к. , т. к. 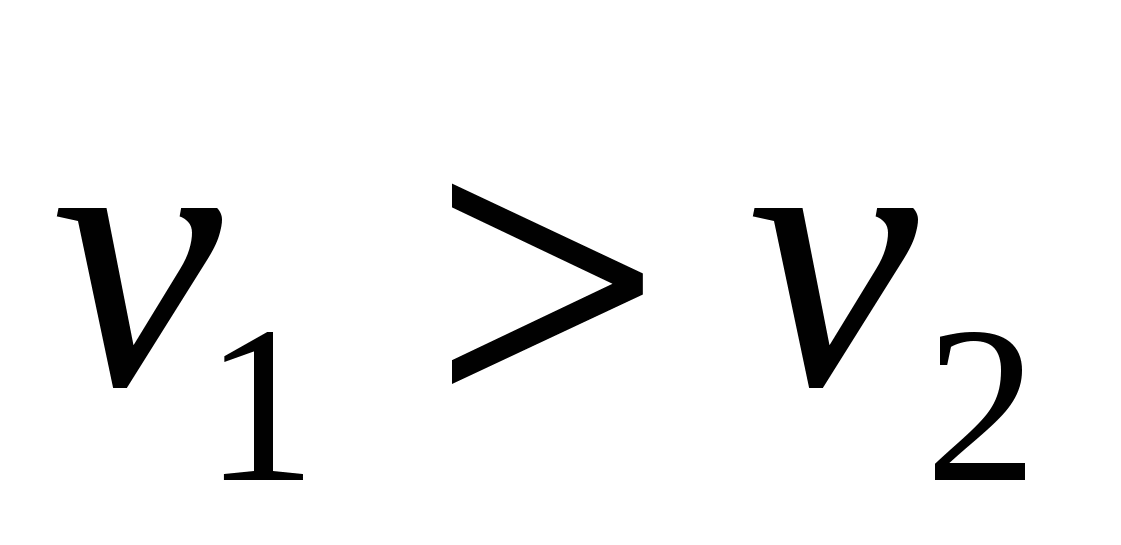 , то изменение количества движения протекшей массы составит , то изменение количества движения протекшей массы составит 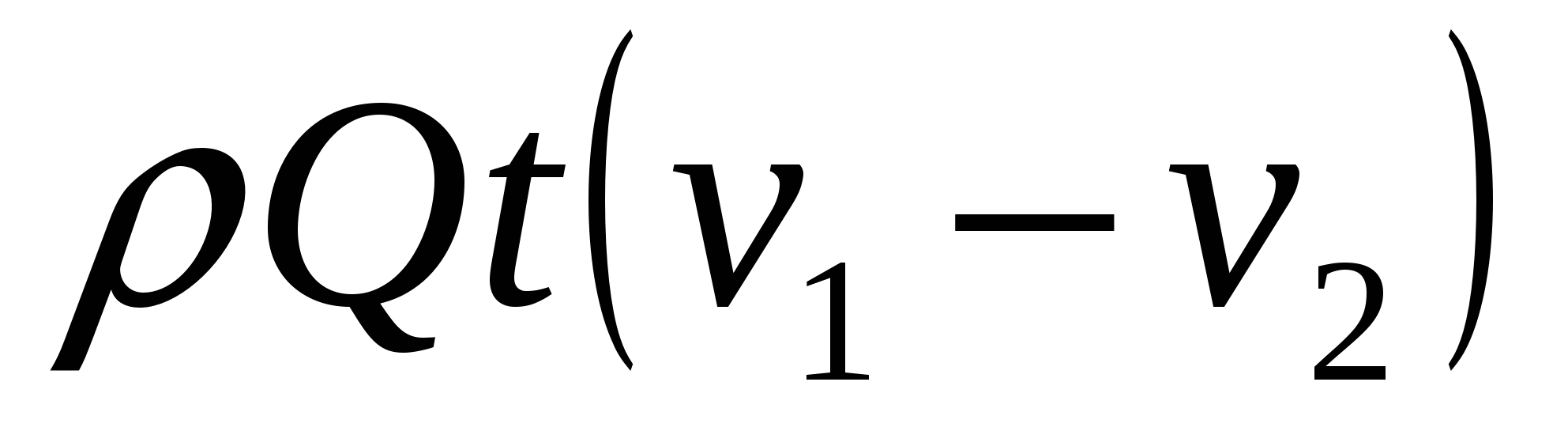 .(а) .(а)
Это изменение количества движения равно импульсу сил давления. Эти силы следующие: в сечении 1-1, где давление 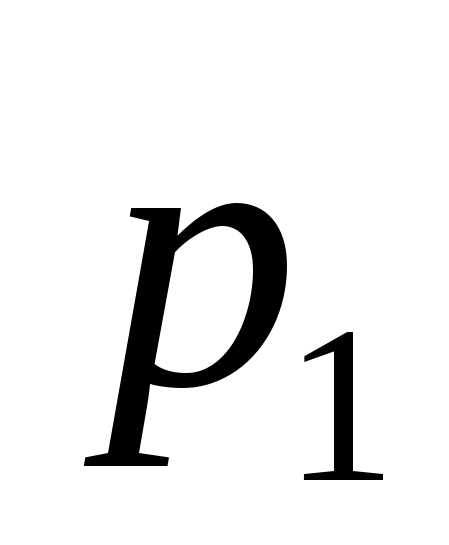 ,сила давления направлена в сторону течения и равна ,сила давления направлена в сторону течения и равна 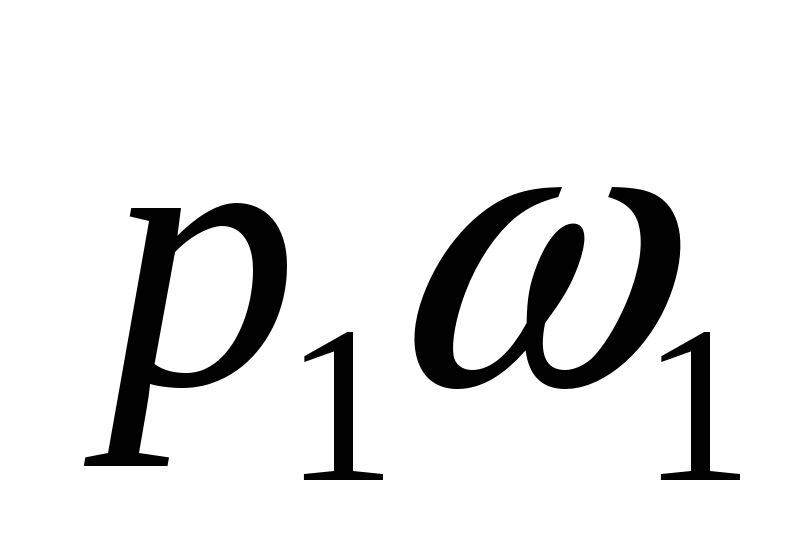 (считается, что давление (считается, что давление 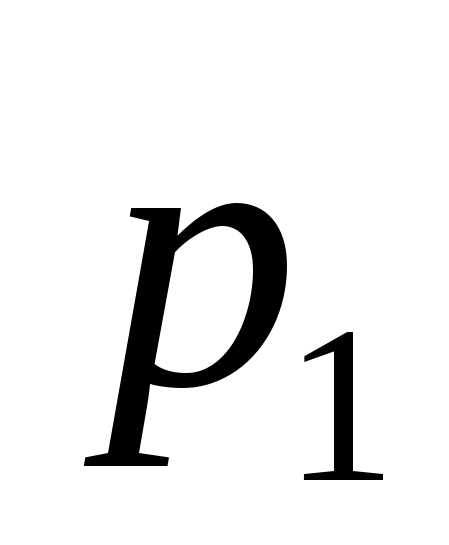 действует и на поперечной стенке). Сила давления в сечении 2-2 направлена против течения и равна действует и на поперечной стенке). Сила давления в сечении 2-2 направлена против течения и равна 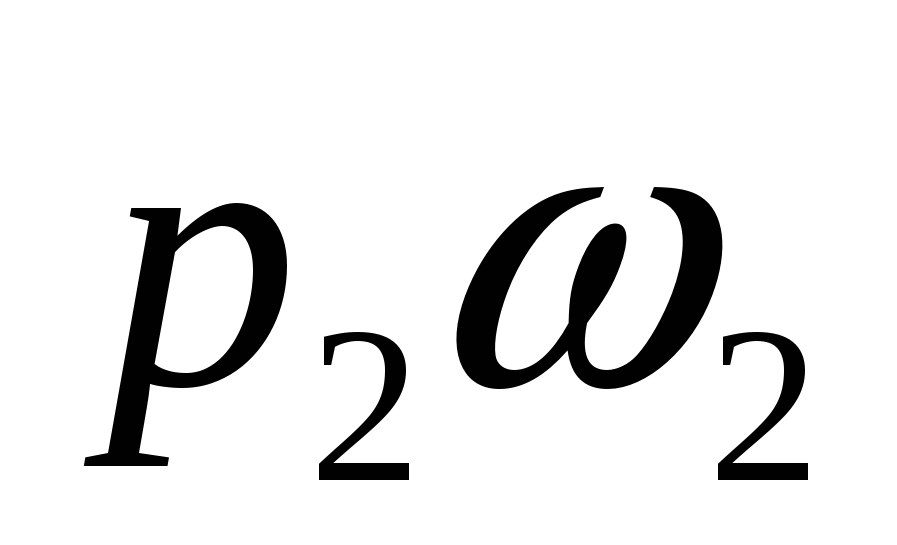 . Суммарный импульс этих сил за время tсоставляет . Суммарный импульс этих сил за время tсоставляет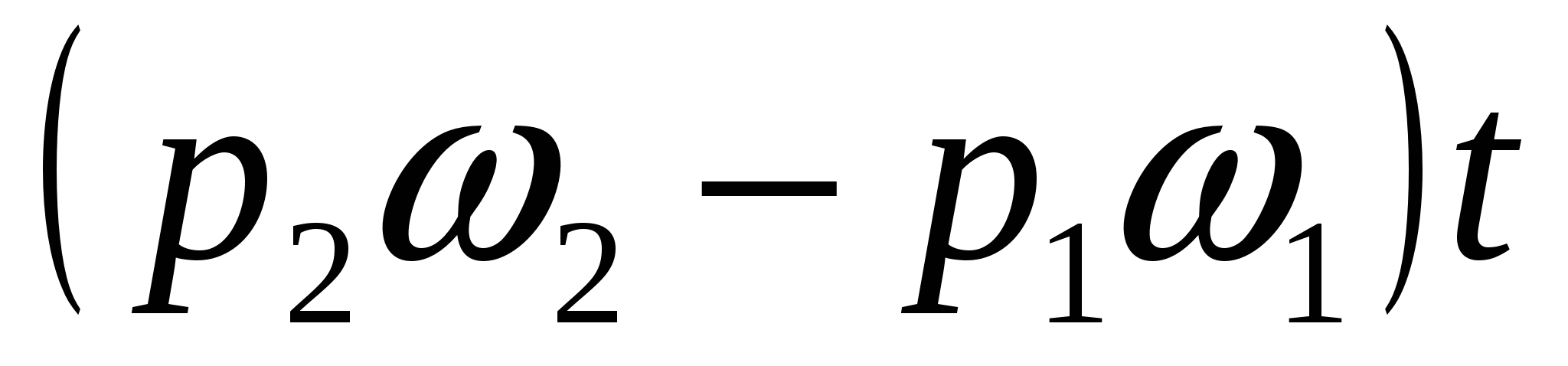 . (б) . (б)
В соответствии с теоремой о количестве движения приравниваем выражения (а) и (б)
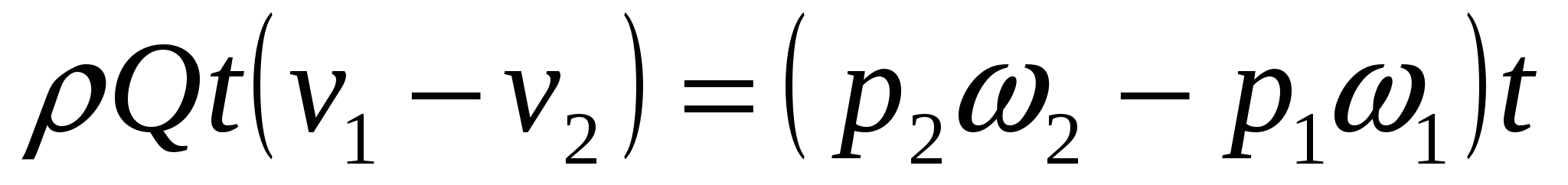
Отсюда после деления на 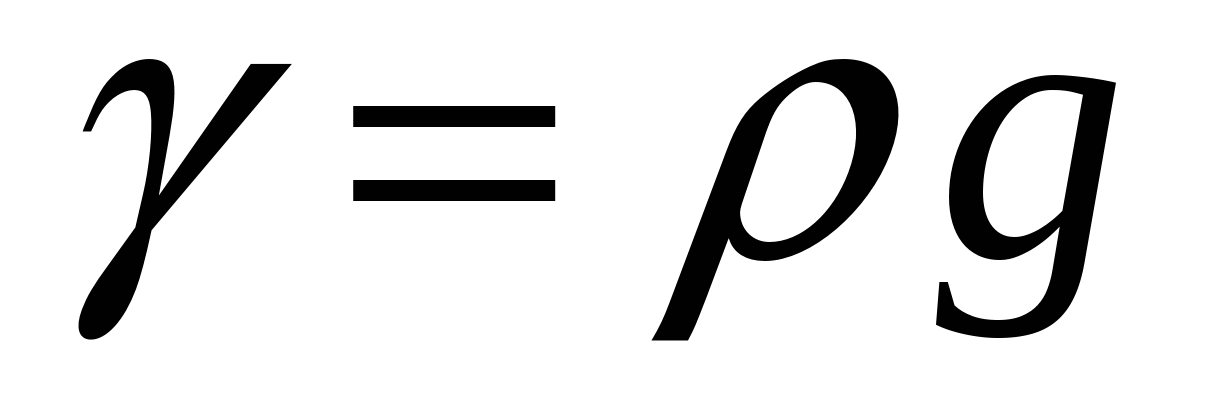 и на и на 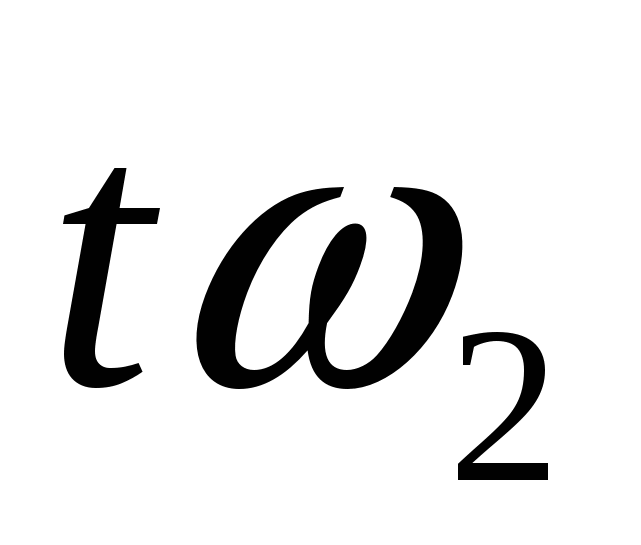 и перемены знаков получаем и перемены знаков получаем
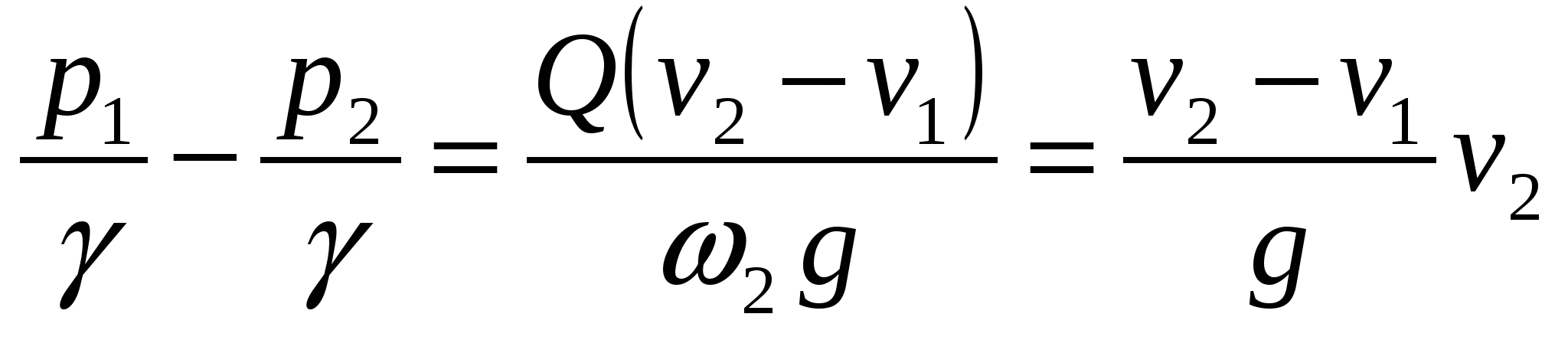 , (104) , (104)
так как 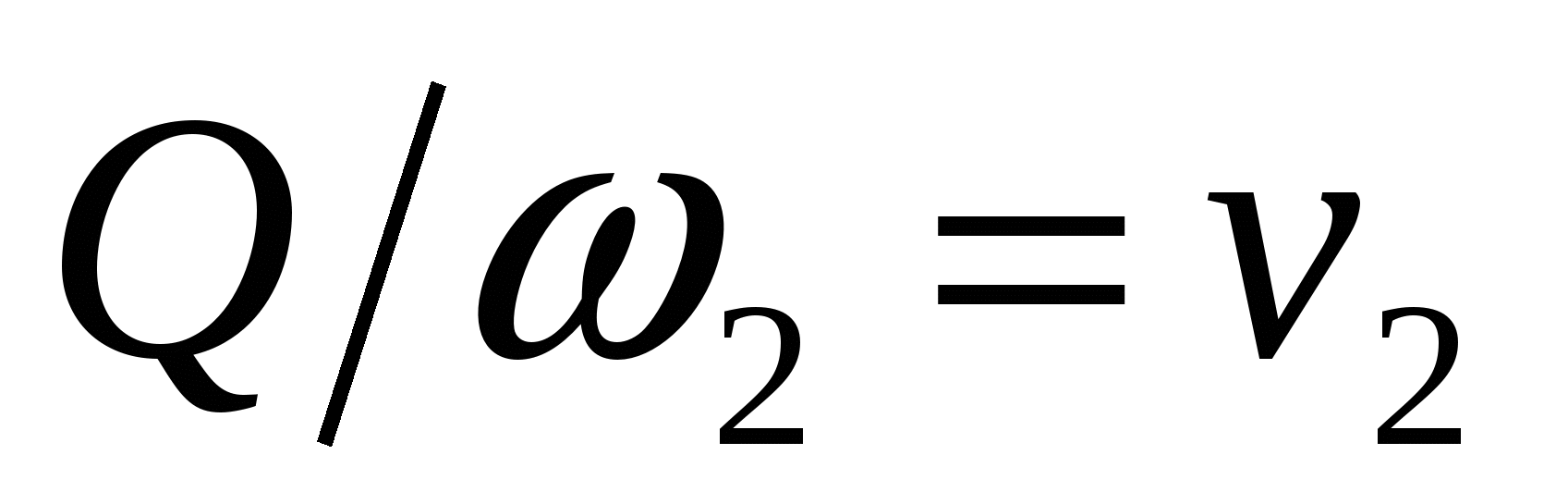 . .
Подставляя правую часть равенства (б) в выражение (а), имеем
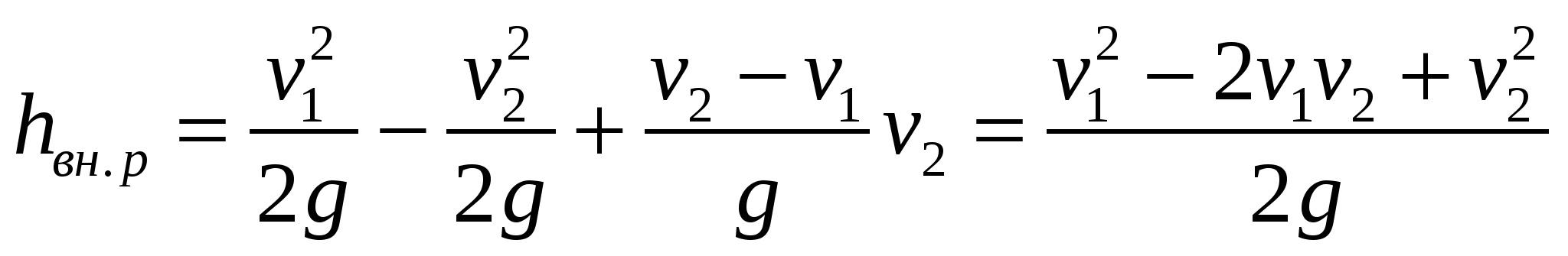
или окончательно 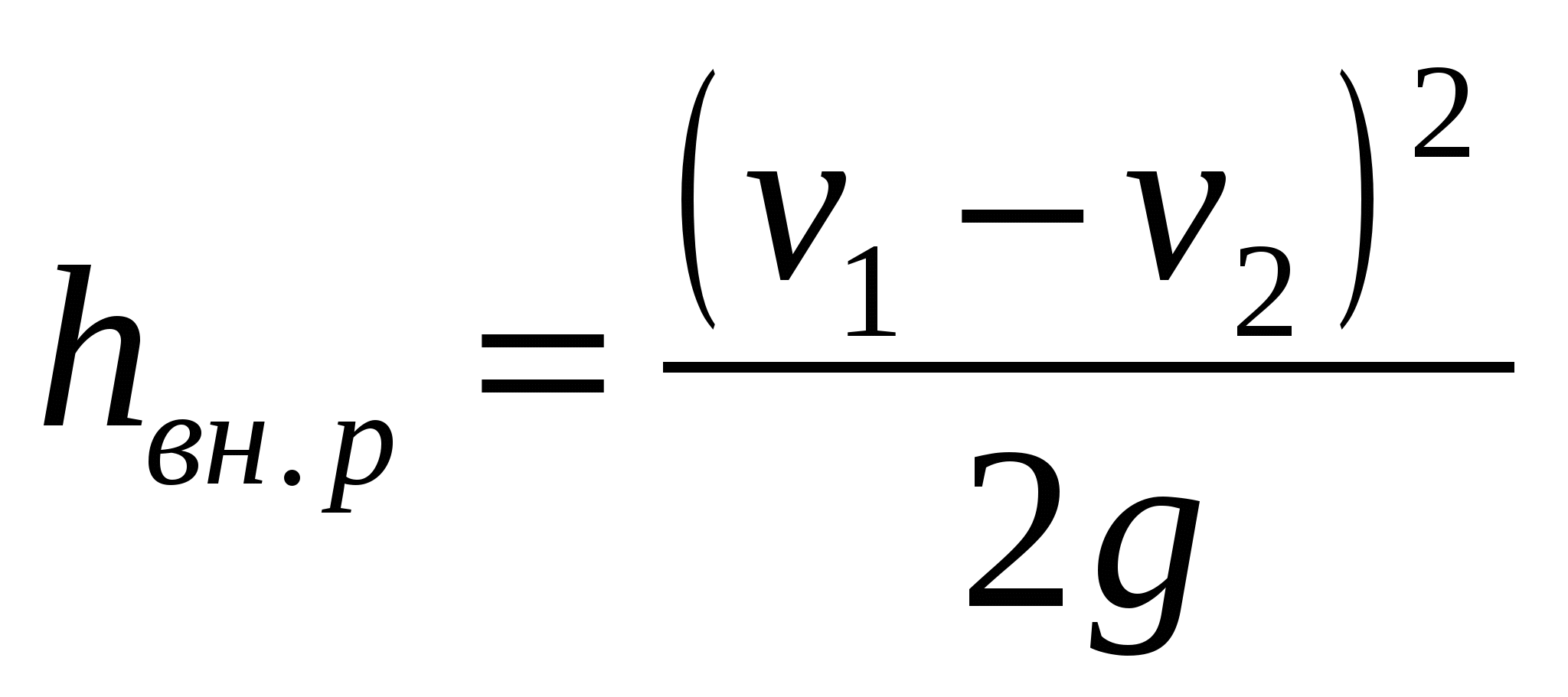 , ,
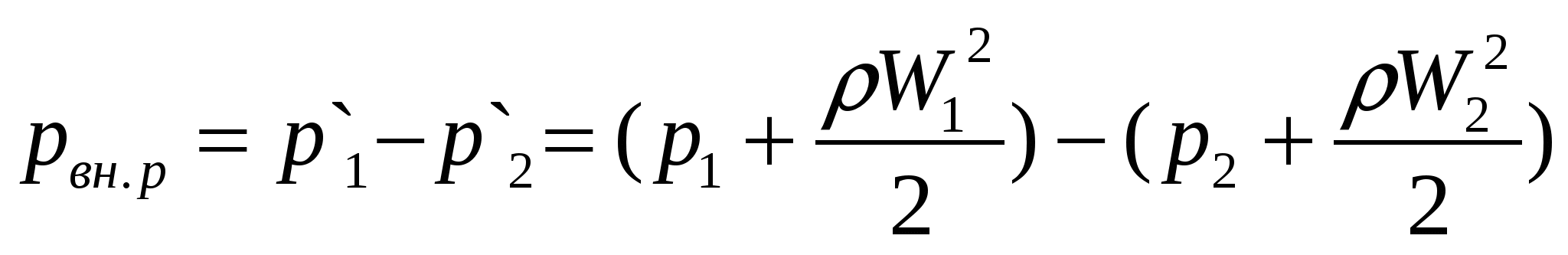
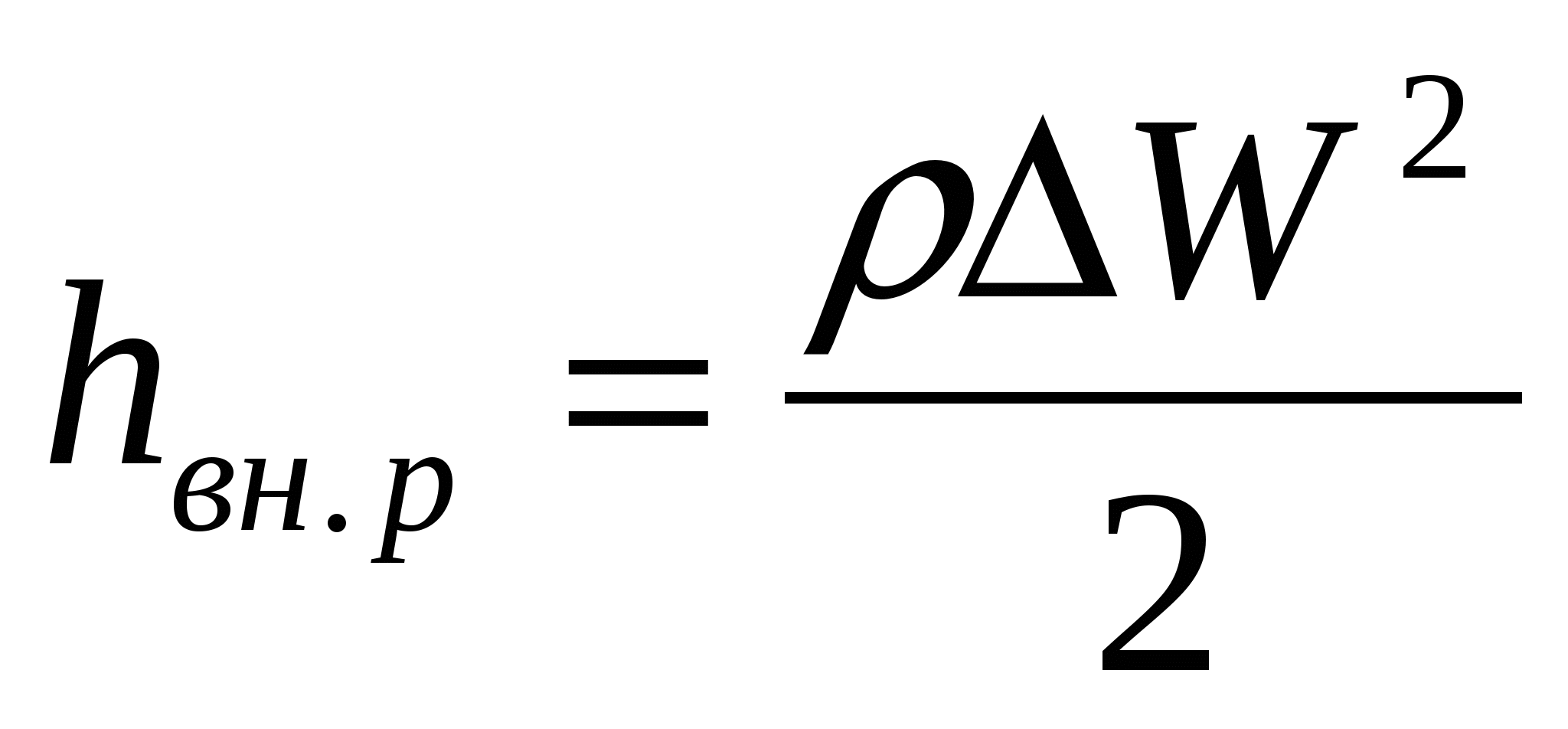 (106) (106)
т. е. потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Уравнение (106) называется формулой Борда.
Для выявления значения коэффициента местного сопротивления из уравнения (106) вынесем за скобки 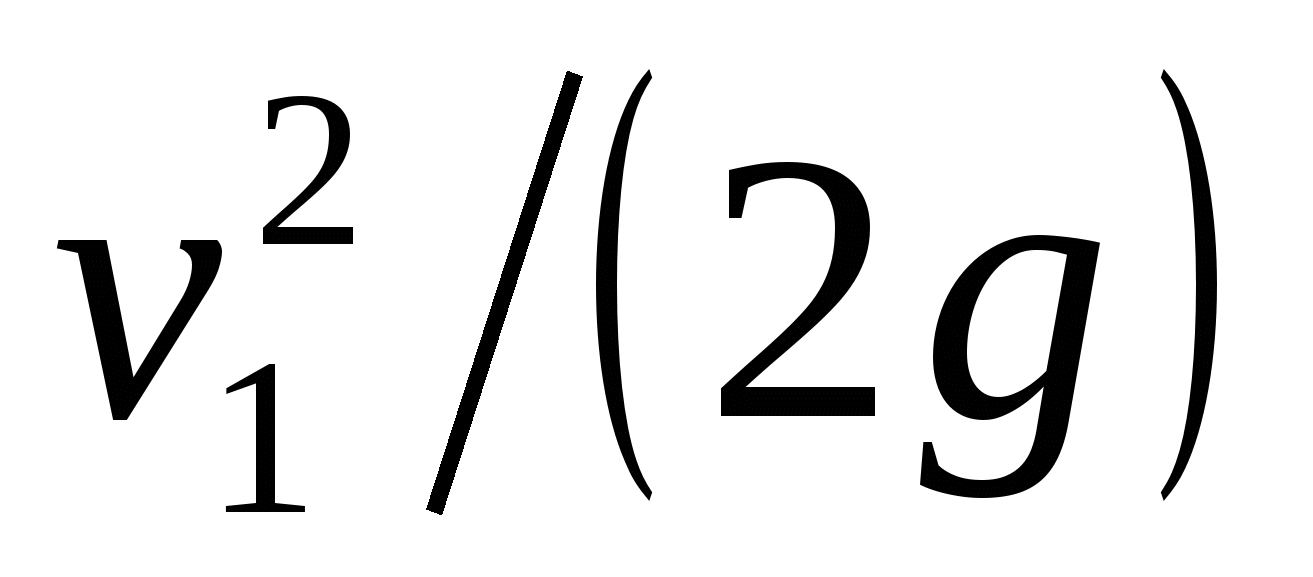 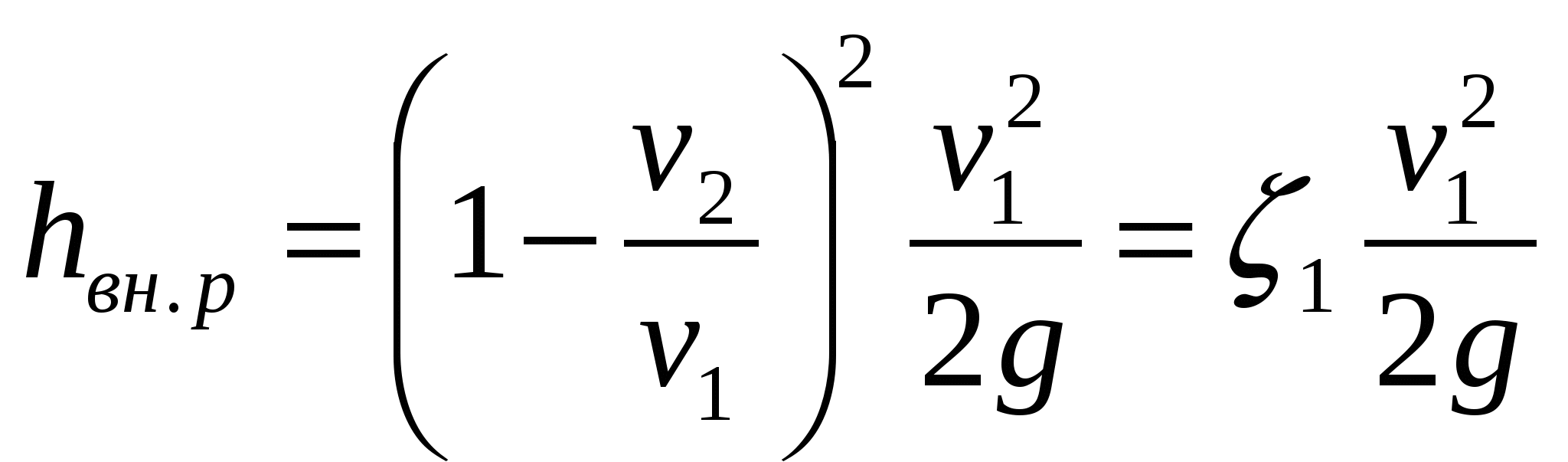 , или , или 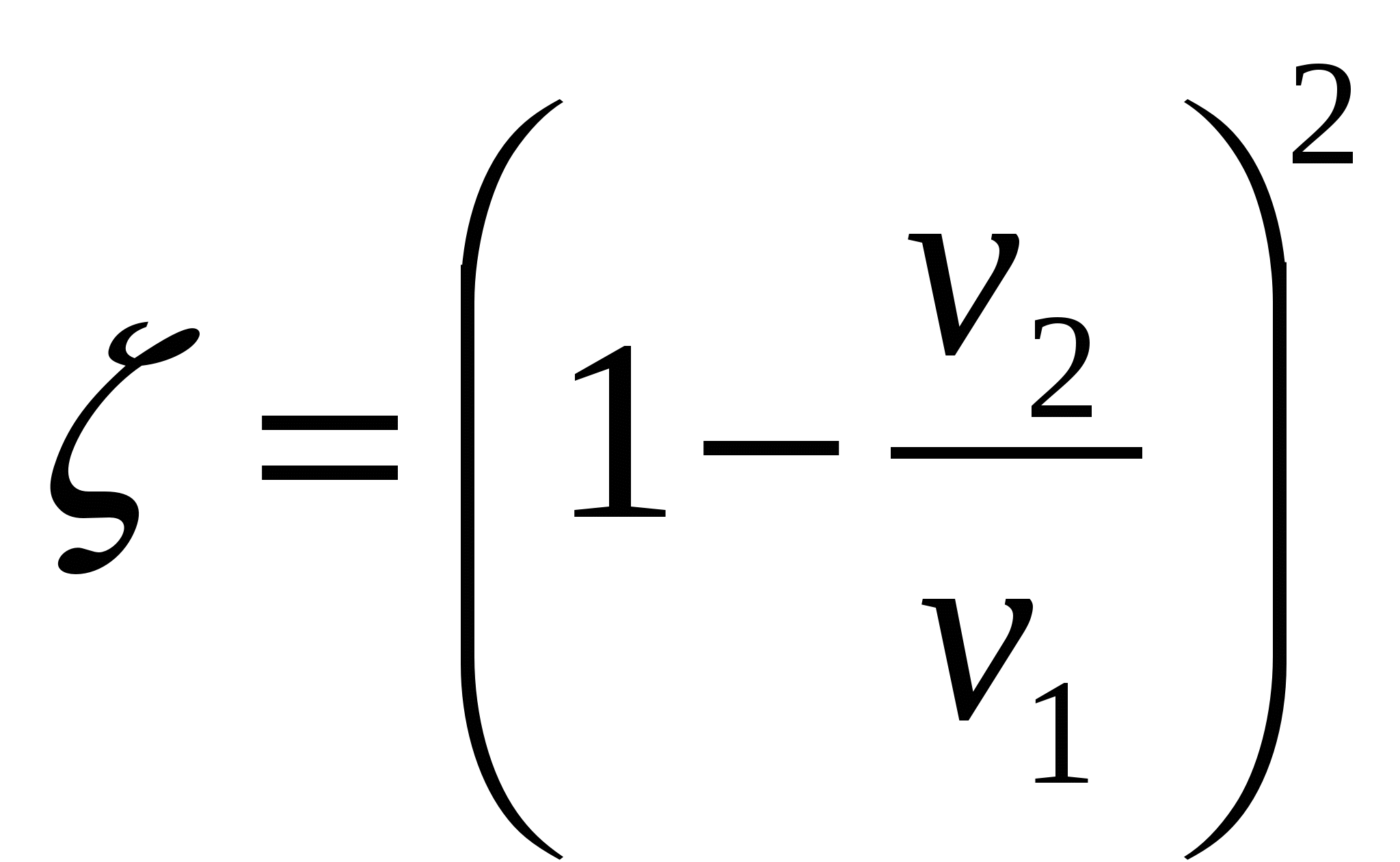 . .
Заменяя скорости через площади живых сечений из уравнения неразрывности 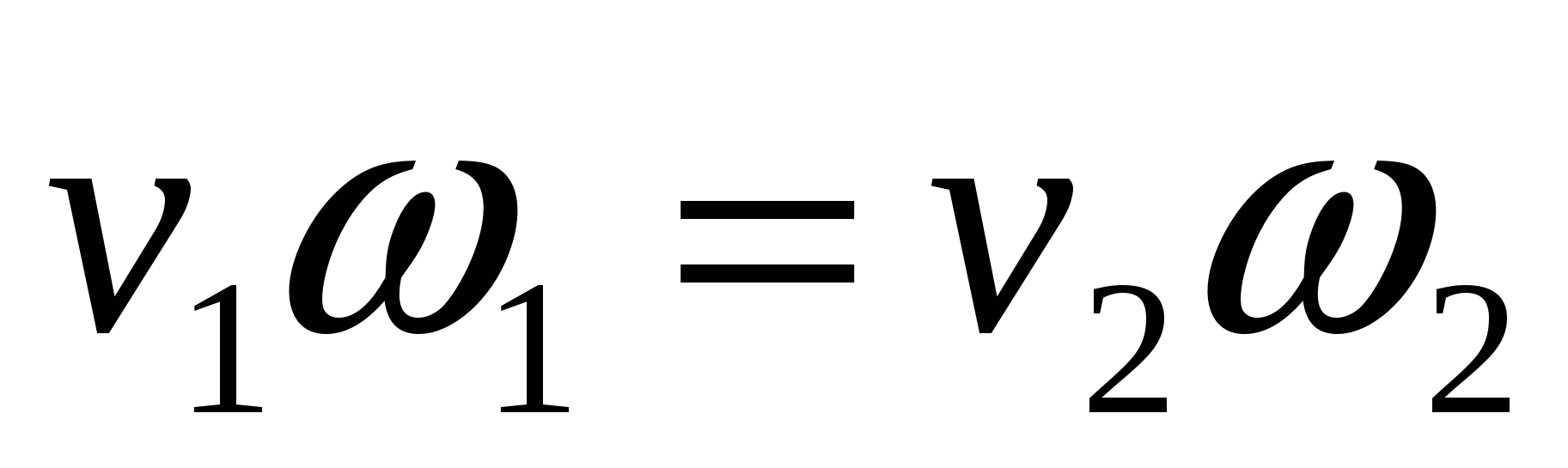 , получим , получим
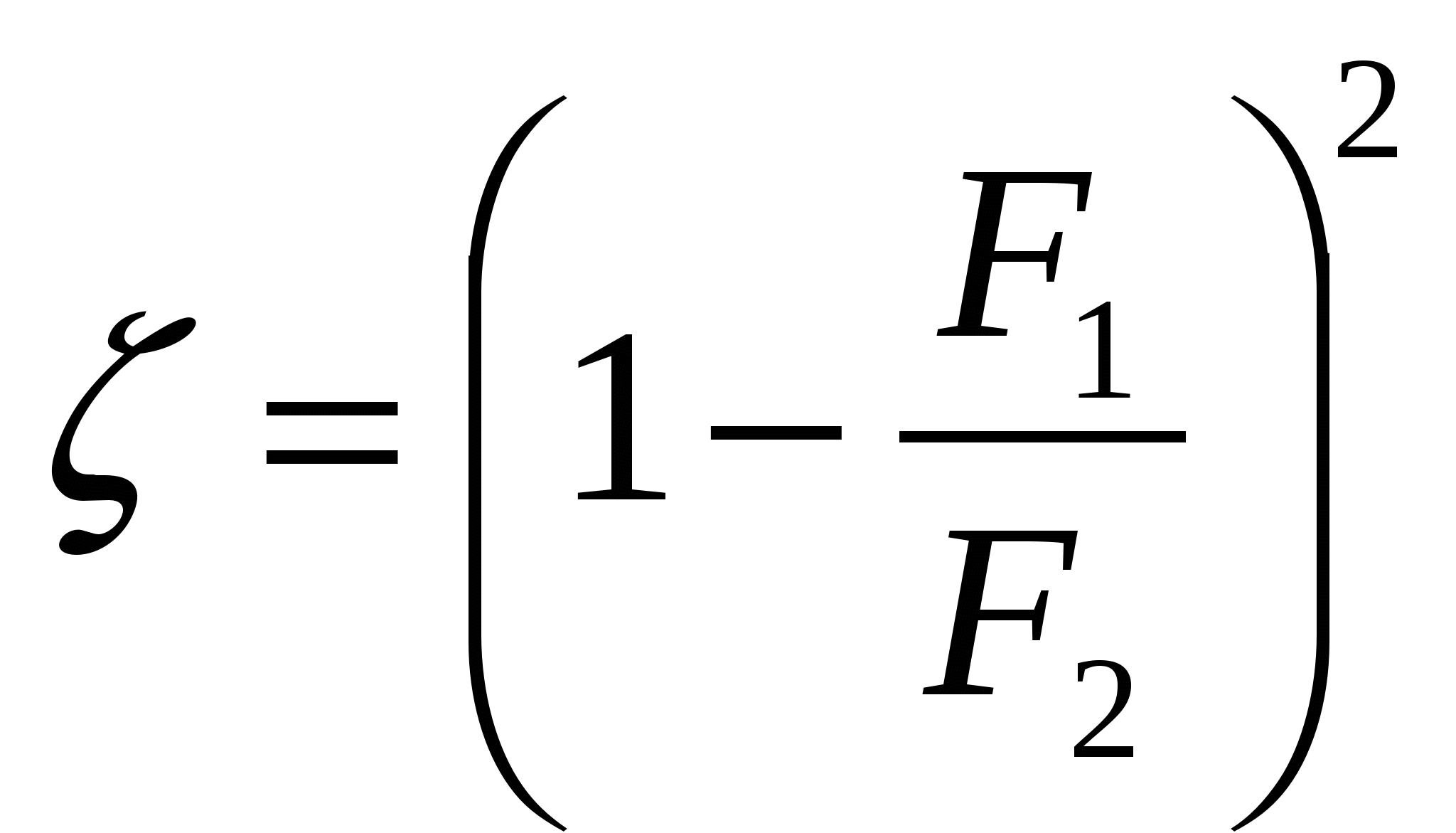 . .
3. Равновесие жидкости при наличии негравитационных массовых сил.
Т.е. кроме сил тяжести действуют еще и силы инерции. Относительный покой - случаи, когда жидкость неподвижна относительно стенок сосудов, движущихся с ускорением.
1. Сосуд с жидкостью движется в горизонтальном направлении с ускорением  . Найдем зависимость для поверхности уровня p=const. Дифференциальное уравнение изобарических поверхностей получим в виде: Xdx+Ydy+Zdz=0. В координатах проекции напряжений массовых сил будут: X=-a, Y=0, Z=-g. Уравнение поверхностей: (a/g)x+z=const. Семейство полуплоскостей, наклоненных под углом , причем tg=a/g. . Найдем зависимость для поверхности уровня p=const. Дифференциальное уравнение изобарических поверхностей получим в виде: Xdx+Ydy+Zdz=0. В координатах проекции напряжений массовых сил будут: X=-a, Y=0, Z=-g. Уравнение поверхностей: (a/g)x+z=const. Семейство полуплоскостей, наклоненных под углом , причем tg=a/g.
2. Цилиндрический сосуд с жидкостью равномерно вращается вокруг вертикальной оси с угловой скоростью . В этом случае проекции напряжений массовых сил будут X=²x, Y=²y, Z=-g, а уравнение после интегрирование примет вид 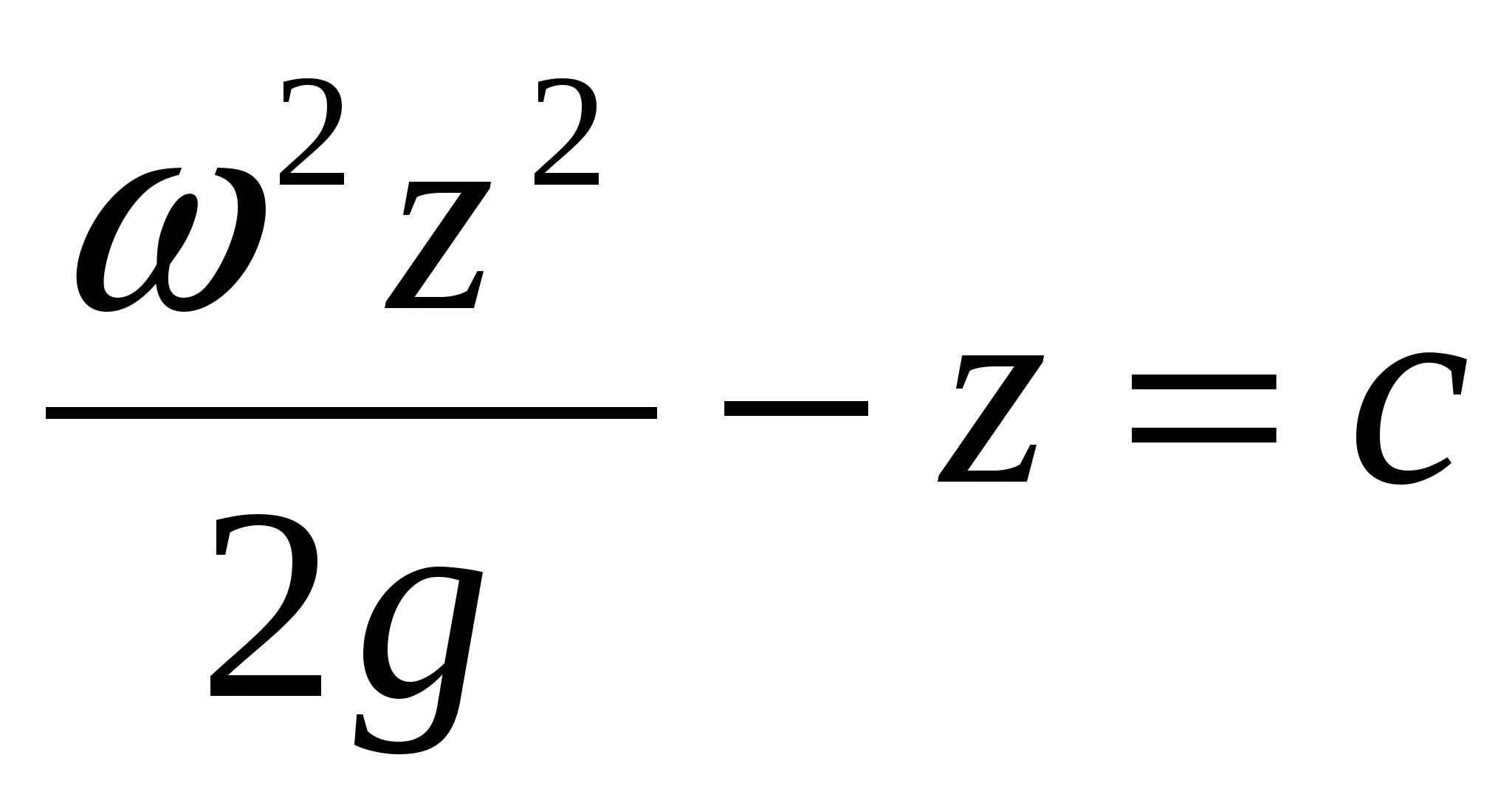 .При z=0, z=h и C=-h. Уравнение поверхностей примет вид: .При z=0, z=h и C=-h. Уравнение поверхностей примет вид: 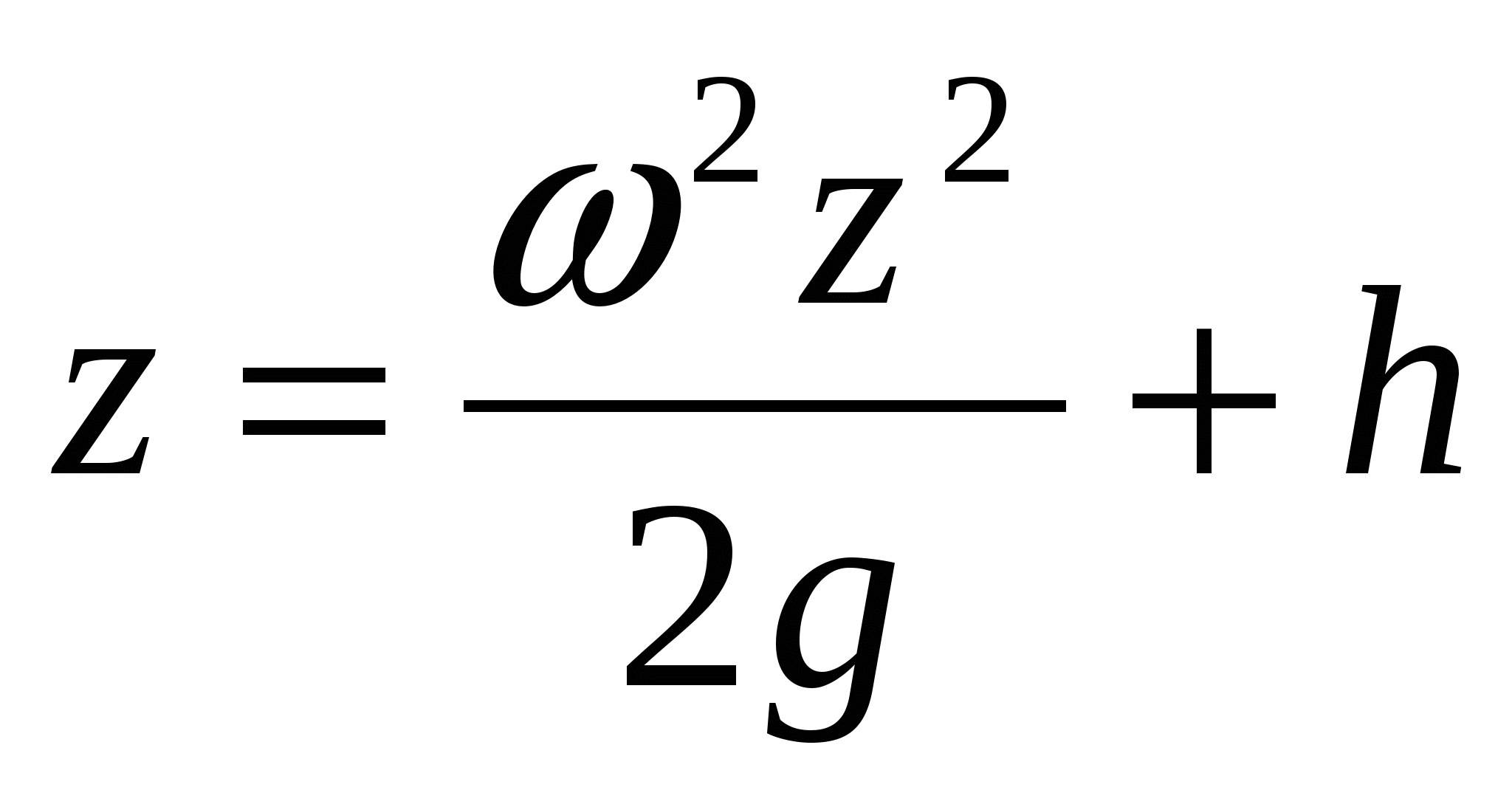 . .
Билет 21.
1. Вихревая линия, вихревая трубка, вихревой шнур.
Вихревая линия – это линия в пространстве, направление касательной к которой для данного момента времени в каждой точке совпадает с направлением вектора вихря скорости в этой точке. Вихревая линия – это пространственная кривая, где векторы угловых скоростей жидкий частиц касательны к ней в каждой точке пространства в данный момент времени. Дифференциальное уравнение вихревой линии 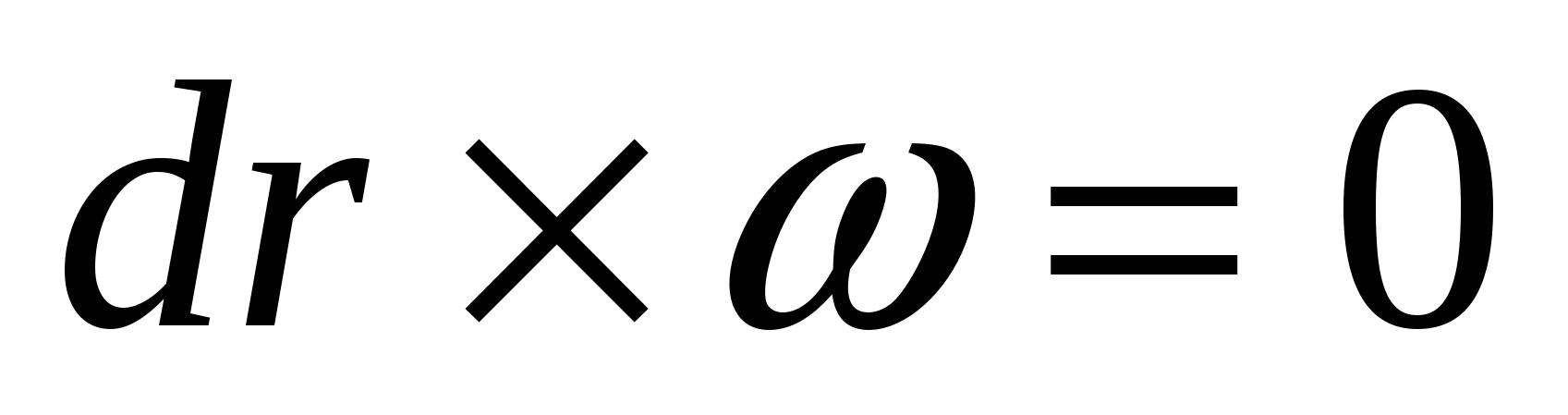 или dx/x= dy/y =dz/я. или dx/x= dy/y =dz/я.
Вихревая трубка охватывает область течения, где наблюдается вращение частиц. Ее боковая поверхность состоит из вихревых линий. Пучок вихревых линий внутри вихревой трубки называется вихревым шнуром.
3. Дивергенция скорости: физические интерпретации.
Дивергенция означает расхождение: 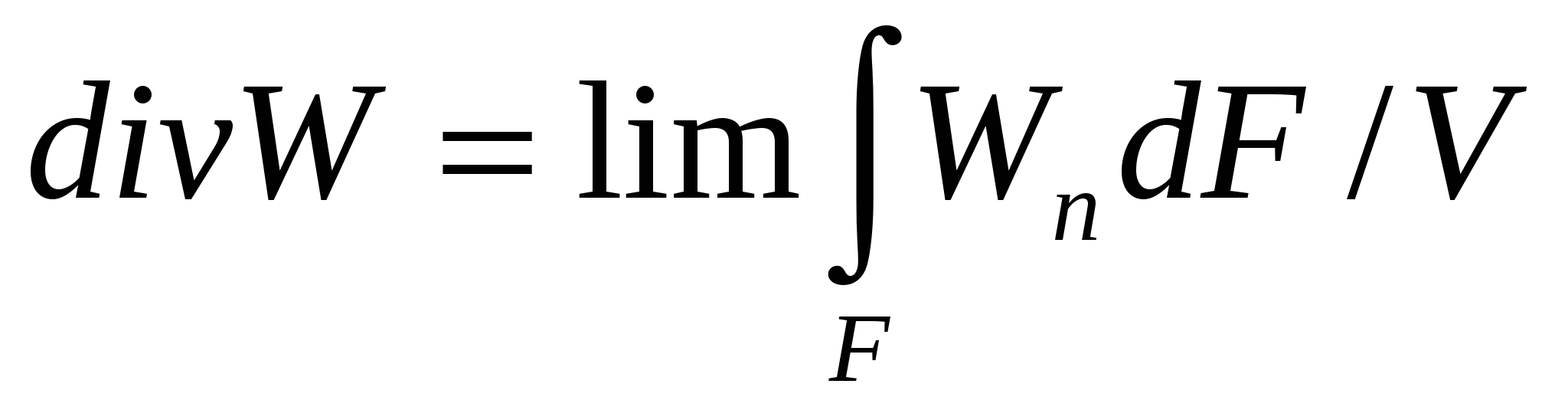 . .
Физический смысл: количество жидкости, возникающей или исчезающей в области окружающей т.М.
Дивергенция, величина скалярная:
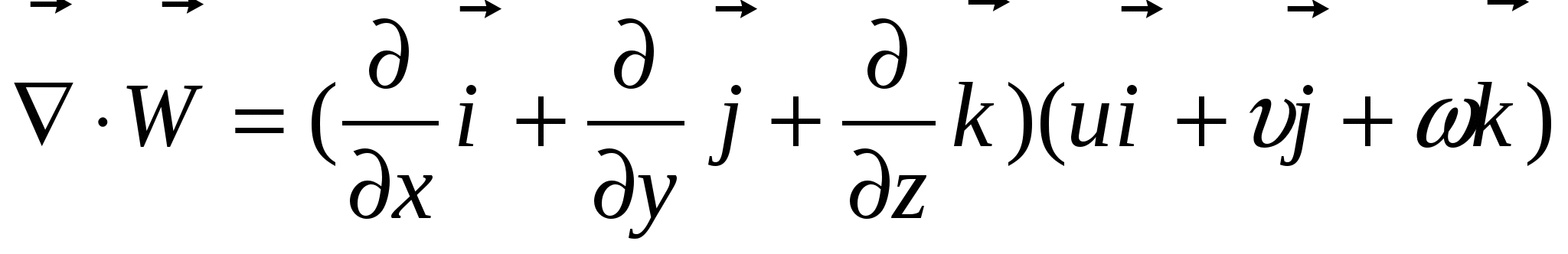 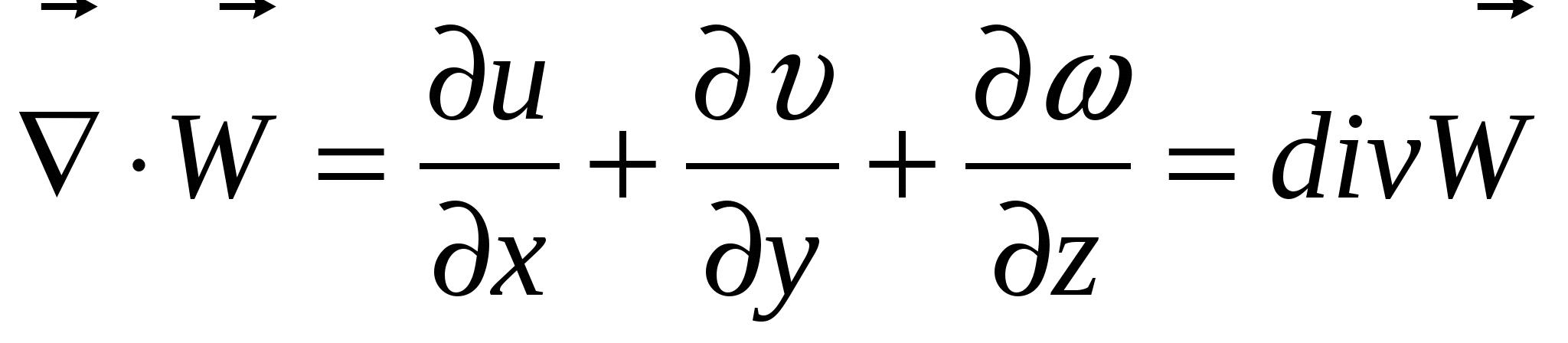 Формула Остроградского - Гаусса: для произвольного вектора Формула Остроградского - Гаусса: для произвольного вектора  установлена связь между объемным и поверхностным интегралом:. установлена связь между объемным и поверхностным интегралом:.
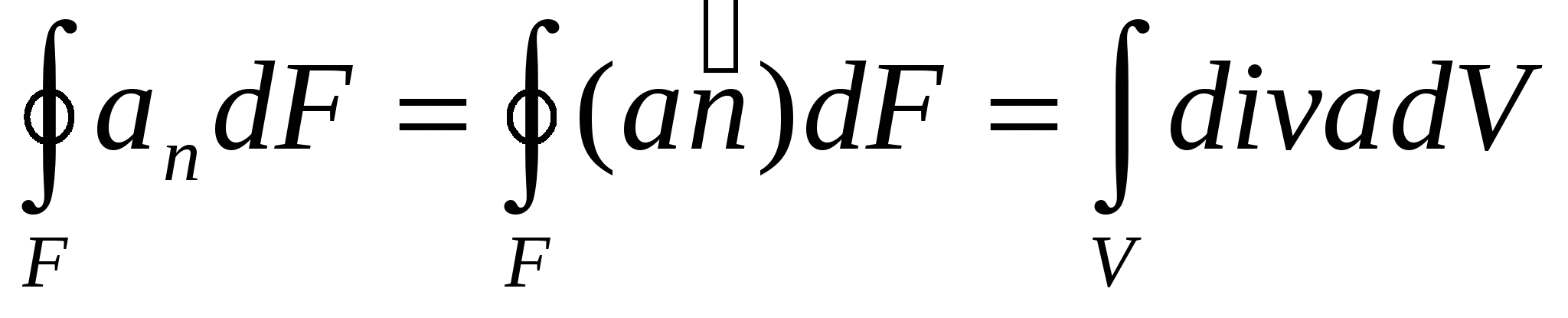
Билет 23.
1.23 Критерий Ренольдса и его физический смысл. Случаи его использования как критерия для определения режима течения жидкости.
Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока
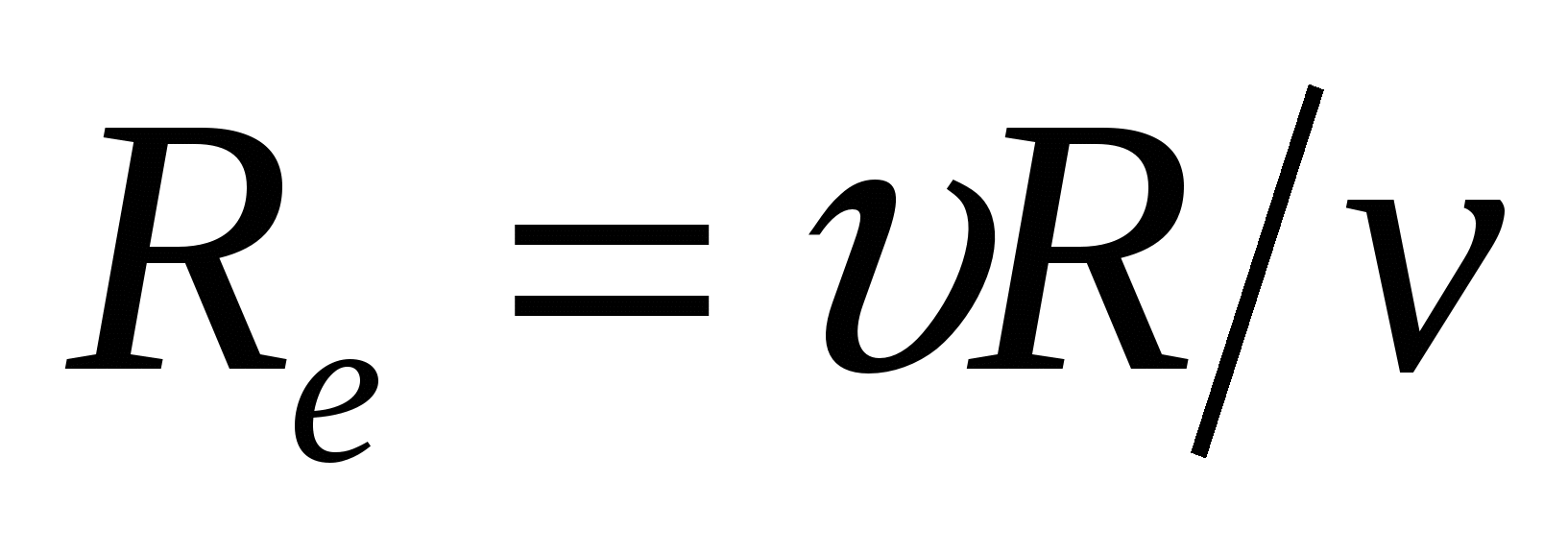 , (1) , (1)
где 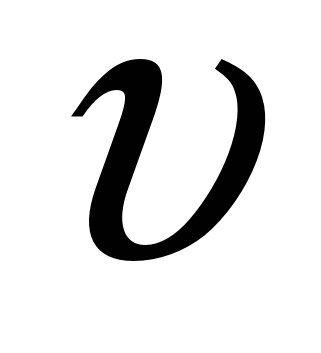 – скорость, м/сек; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м2/сек. – скорость, м/сек; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м2/сек.
Это отношение называется числом Рейнолъдса. Значение числа Re, при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса ReKp.
Если фактическое значение числа Re, вычисленного по формуле (1), будет больше критического Re > ReKp – режим движения турбулентный, когда Re < ReKp – режим ламинарный.
Для напорного движения в цилиндрических трубах удобнее число Рейнольдса определять по отношению к диаметру d, т. е.
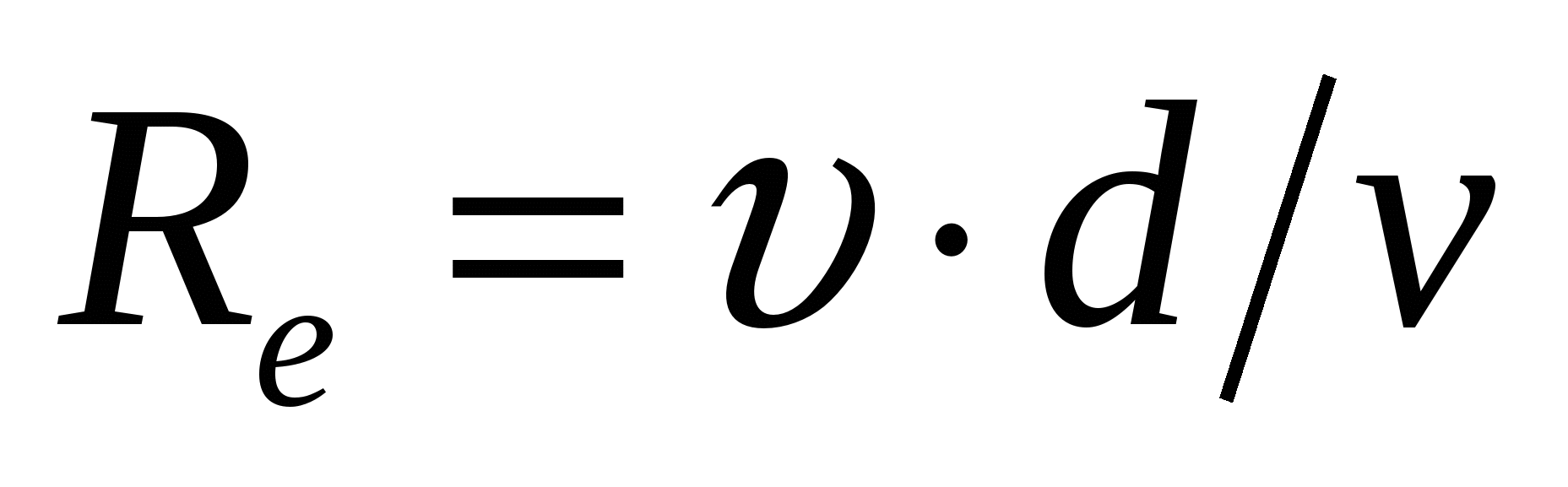 , (2) , (2)
где d – диаметр трубы.
В этом случае ReKpполучается равным
2300. Если в формуле (2) для трубопроводов круглого сечения dвыразить через гидравлический радиус 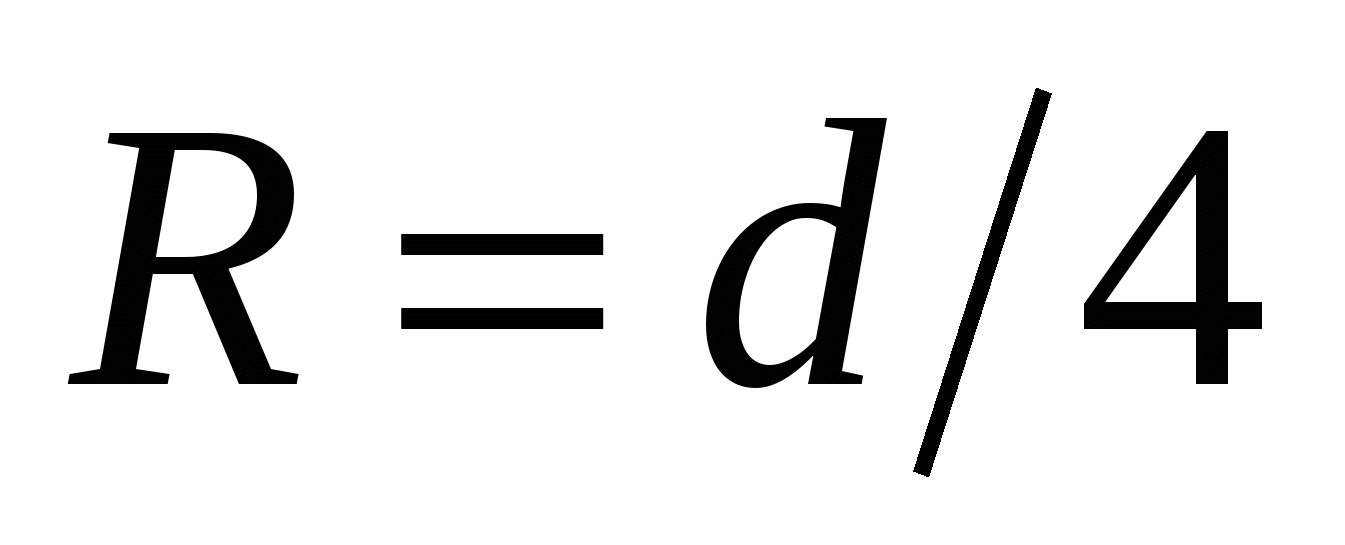 ,то получим ReKp=575. Для других трубопроводов и каналов некруглых сечений можно принимать значение критического числа Рейнольдса ReKp=300 (при вычислении Reчерез гидравлический радиус). ,то получим ReKp=575. Для других трубопроводов и каналов некруглых сечений можно принимать значение критического числа Рейнольдса ReKp=300 (при вычислении Reчерез гидравлический радиус).
2. Схема Прандтля пульсационного движения в турбулентном потоке. Формула Прандтля.
В 1904г. Прандтль предложил 2-х сложную модель турбулентности согласно ей в непосредственной близости от стенки область вязкого подслоя с ламинарным течением: в = du/dy, а m =0. В части потока, удаленного от стенки, наоборот, m = du/dy, а в =0.
Более поздние исследования показали, что есть некоторая область, где эти напряжения имеют один порядок: =в +m =( + m) du/dy.
Чтобы раскрыть зависимость ` xy =m =-u`v` Прандтль в 1924 г. Предложил следующую схему пульсационного движения в турбулентном потоке: жидкий моль, двигавшийся в слое 1 с осредненной скоростью 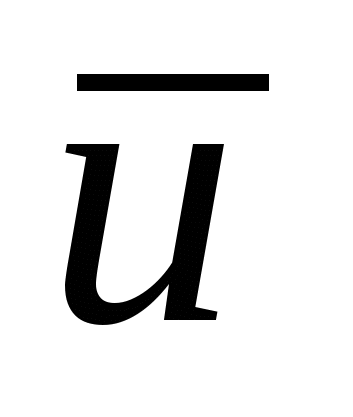 , под влиянием турбулентной пульсации , под влиянием турбулентной пульсации 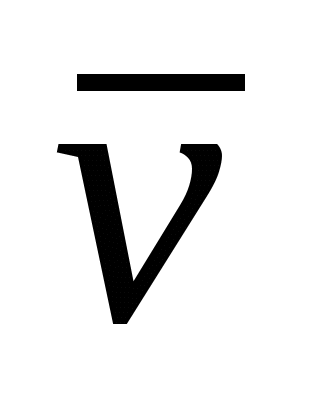 , перемещающейся на расстояние l` в слое 2. Пи этом перемещении моль не взаимодействует с другими частицами, а в слое 2 приобретает осредненную скорость , перемещающейся на расстояние l` в слое 2. Пи этом перемещении моль не взаимодействует с другими частицами, а в слое 2 приобретает осредненную скорость 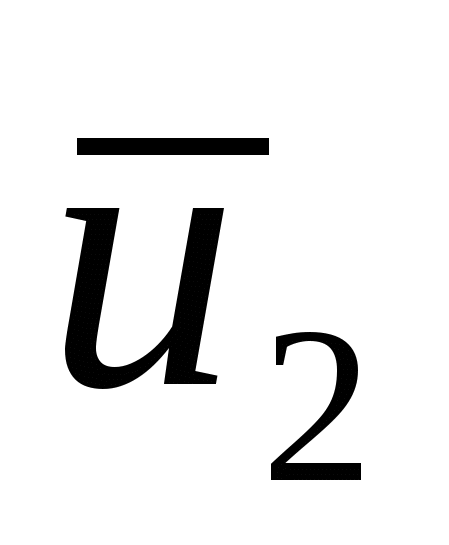 . В результате в слое 2 появляется пульсация продольной скорости . В результате в слое 2 появляется пульсация продольной скорости 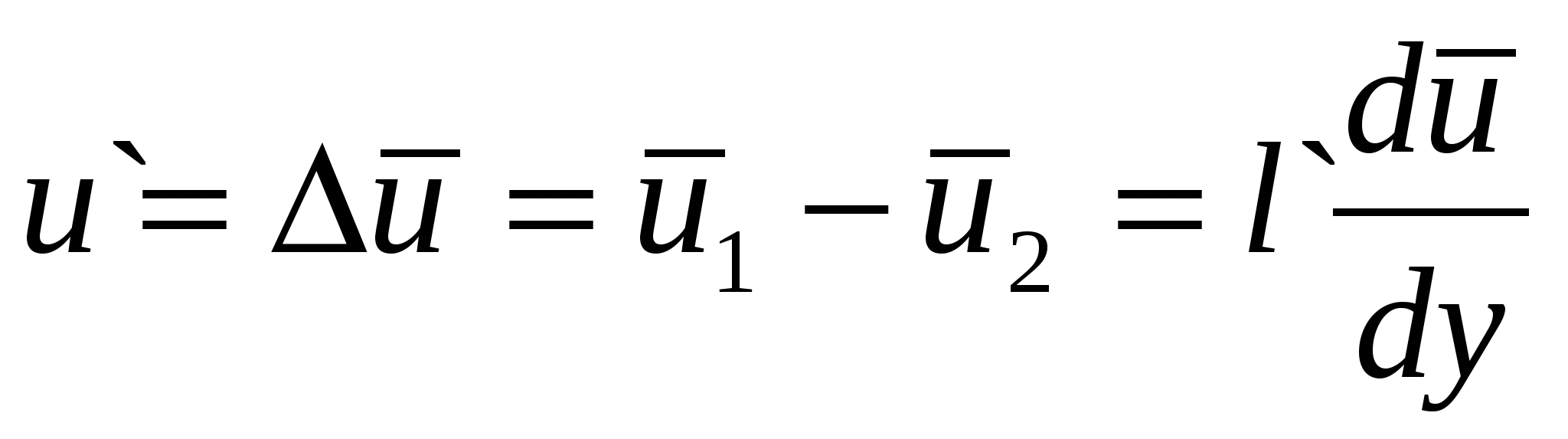 . .
В общем случае пульсация появляется как в продольном, так и в поперечном направлениях.
Предполагая, что u` и v` величины одного порядка и осредняя их получим: 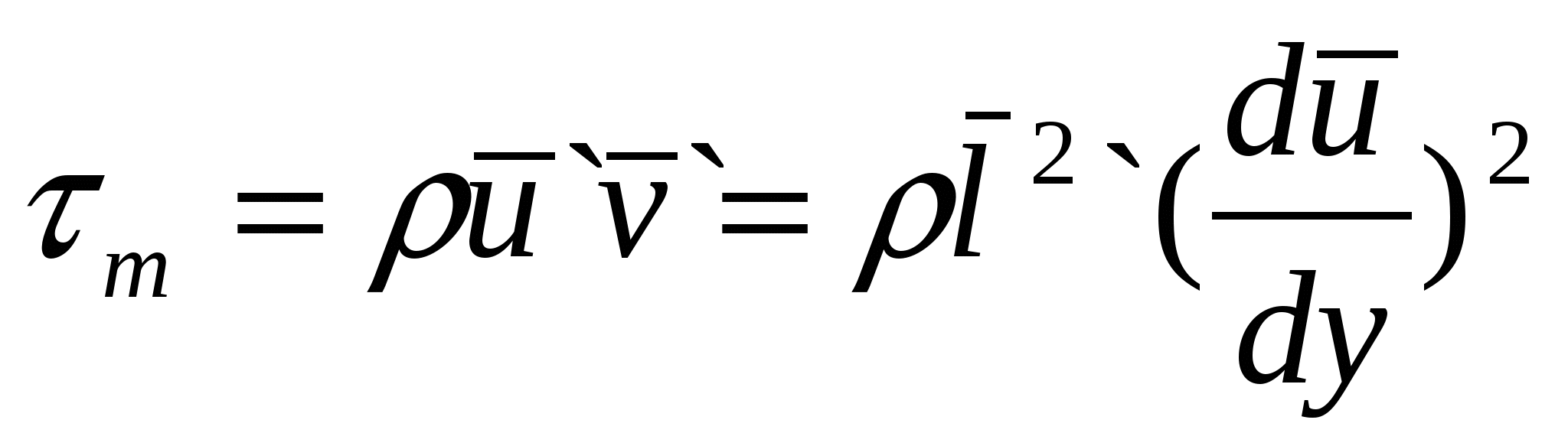 . Введя коэффициент пропорциональности k и полагая: . Введя коэффициент пропорциональности k и полагая: 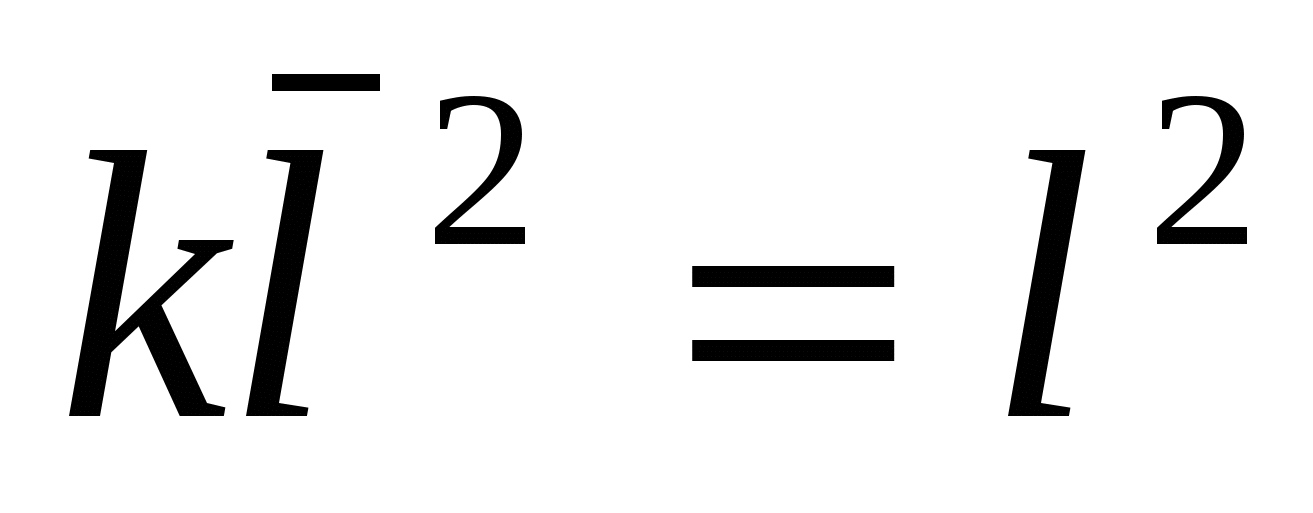 , получим формулу Прандтля: , получим формулу Прандтля: 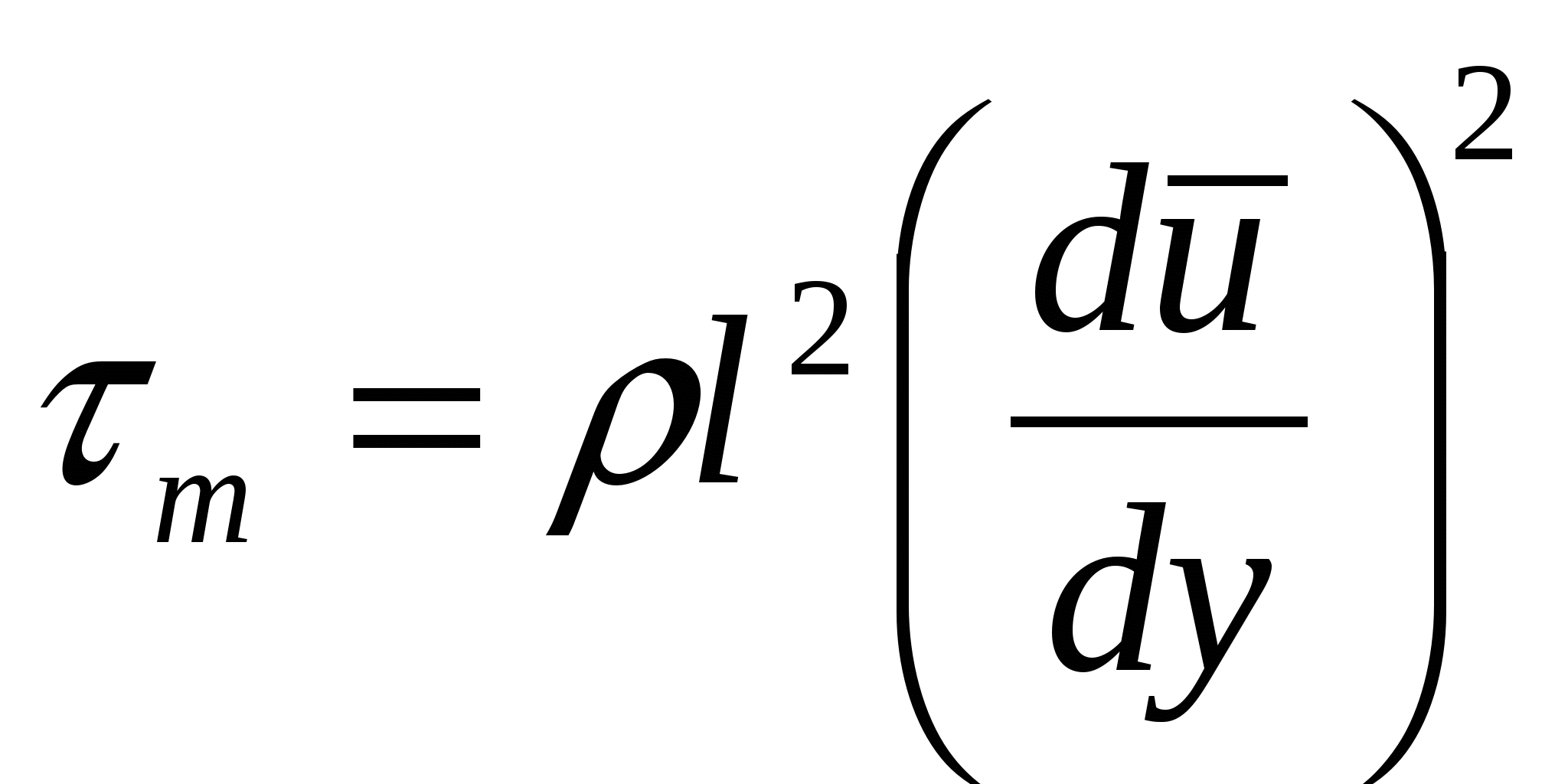 . Величина l, имеющая линейную размерность, называется длиной пути смешения. Она характеризует возможность для жидких молей перемещаться в поперечном направлении с сохранениями исходной скорости и является характеристикой. . Величина l, имеющая линейную размерность, называется длиной пути смешения. Она характеризует возможность для жидких молей перемещаться в поперечном направлении с сохранениями исходной скорости и является характеристикой. |
 Скачать 0.89 Mb.
Скачать 0.89 Mb.