Шпоры по гидравлике. Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется

• Название: Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется
• Дата: 27.02.2019
• Размер: 0.89 Mb.
• Имя файла: Шпоры по гидравлике.doc
• Тип: Документы; #69072
• страница: 6 из 7

2. Вторая теорема Гельмгольца (без доказательства) и следствие из нее. Теорема Стокса (без доказательства) о связи между интенсивностью вихревого движения и циркуляцией.

Вторая теорема Гельмгольца о сохранении вихревых линий: Если принять условие теоремы Томпсона, то можно утверждать, что 1) интенсивность вихревой трубки во все время движения остается постоянной, 2) интенсивность вихревой трубки постоянна вдоль всей ее длины, т.е. циркуляция скорости по любому контуру, охватывающему трубку, постоянна.



Интенсивность вихревого шнура или вихревой трубки:

Если вектор  в сечении F постоянен, то для элементарной вихревой трубки: .

Следствия теоремы Гельмгольца: 1) чем меньше площадь сечения вихревой трубки, тем больше интенсивность вихревой трубки (угловая скорость). Но сечение вихревой трубки нигде не может быть равной нулю, т.к. в этом случае интенсивность вихревой трубки была бы равна бесконечности, что физически не выполнимо; 2) вихревые трубки не могут заканчиваться внутри жидкости – они либо замыкаются на себя, как кольца табачного дыма, либо опираются на свободную поверхность жидкости или твердого тела, или уходят в бесконечность.

Теорема Стокса утверждает, что интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, опоясывающему вихревую трубку один раз по ее поверхности так, что его можно стянуть в точку не выходя за пределы жидкости:

Следствия теоремы Стокса: 1. Если контур охватывает несколько вихревых трубок или областей, то циркуляция скорости по этому контуру равна алгебраической сумме циркуляции по контурам, охватывающим каждую вихревую область отдельно. 2. Если внутри рассматриваемой области течение безвихревое, то циркуляция скорости по любому замкнутому контуру в этой области равна нулю.
3. Особенности движения жидкой среды как деформируемой среды.

Жидкости по молекулярному строению занимают промежуточное положение между кристаллическим твердым телом и газом . Поэтому они обладают плотностью близкой к твердому телу, устойчиво сохраняют величину занимаемого ими объема, но не держат форму.

Сложность молекулярного строения жидкости затрудняет получение теоретическим путем достаточно общих связей между молекулярными характеристиками и наблюдаемыми свойствами: температурой, давлением плотностью, вязкостью и др. Поэтому в гидродинамике пользуются экспериментально установленными значениями для этих величин и связями между ними.

Основными параметрами, характеризующими термодинамическое состояние жидкости, являются температура Т, давление р и плотность ρ.

Связь между плотностью, тем-ой и давлением устанавливается ур-ем состояния, которое для реальных жид-тей и газов выводится в кинет. теории. Однако ввиду сложности общего ур-я состояния и затруднительности определения входящих в него констант, для качественного анализа свойств этих сред пользуются приближенными теоретическими или эмпирическими уравнениями.

Легкоподвижность – св-во среды неогран. деформ. под действием пост. малой силы.

Билет 4.

1. 
   Безвихревое течение и его связь с потенциальным.
   

Единственное условие безвихревого движения является отсутствие вращения жидких частиц относительно собственных осей. При этом частица могут двигаться по любым траекториям и деформироваться. Математическое выражение: или ; ; .

Т.о. в случае безвихревого течения имеет место потенциал, т.е функцию координат  (x, y, z), частные производные которой по любому направлению n и, след-но, по координатным осям равны соответствующим проекциям вектора скорости:

;… (1)

потенциал скорости полностью определяет поле скоростей: и (2)

Поэтому безвихревое течение жидкости называют также потенциальным. Справедливость равенств (1) доказывается подстановкой значений u,   в (2), в результате чего получаются тождества вида
3. Физический смысл уравнения Навье-Стокса и отдельных его составляющих.

Уравнение Навье-Стокса для случая =const:

(XYZ), (u).

В векторной форме:



Ур-е представляет собой специфическую для вязкой сжимаемой жидкости форму второго закона Ньютона. В левой части уравнения стоят силы, отнесенные к единице массы: это массовые силы , сила давления, силы внутреннего трения. В правой части уравнения стоят отнесенные к единице массы произведения массы на соответствующие ускорения.

Билет 7.

1. Понятие о гидравлически гладких и шероховатых трубах.

Состояние стенок трубы в значитель­ной мере влияет на поведение жидкости в турбу­лентном потоке. Так при ламинарном движении жидкость движется медленно и плавно, спокойно обтекая на своём пути незначительные препятст­вия. Возникающие при этом местные сопротивления настолько ничтожны, что их величи­ной можно пренебречь. В турбулентном же потоке такие малые препятствия служат ис­точником вихревого движения жидкости, что приводит к возрастанию этих малых мест­ных гидравлических сопротивлений, которыми мы в ламинарном потоке пренебрегли. Та­кими малыми препятствиями на стенке трубы являются её неровности. Абсолютная вели­чина таких неровностей зависит от качества обработки трубы. В гидравлике эти неровно­сти называются выступами шероховатости, они обозначаются литерой .

В зависимости от соотношения толщины ламинарной плёнки и величины выступов шероховатости будет меняться характер движения жидкости в потоке. В случае, когда толщина ламинарной плёнки велика по сравнению с величиной выступов шероховатости (, выступы шероховатости погружены в ламинарную плёнку и турбулентному ядру течения они недоступны (их наличие не сказывается на потоке). Такие трубы называются гидравлически гладкими. Когда размер выступов шероховатости превышает толщину ламинарной плёнки, то плёнка теряет свою сплошность, и выступы шероховатости становятся источником многочисленных вихрей, что существенно сказы­вается на потоке жидкости в целом. Такие трубы называются гидравлически шероховаты­ми. Естественно, существует и проме­жуточный вид шероховатости стенки трубы, когда выступы шероховатости становятся соизмеримыми с толщиной ламинарной плёнки ≈.
3. Опыт Рейнольдса: режимы течения вязкой жидкости.

В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь.

Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом.

Установка Рейнольдса для исследования режимов движения жидкости представлена на рис. Сосуд А заполняется испытуемой жидкостью. К сосуду А в нижней его части присоединена стеклянная трубка 1 с краном 2, которым регулируется скорость течения в трубке. Над сосудом А расположен сосуд Б сраствором краски. От сосуда Б отходит трубка 3 скраном 4. Конец трубки 3 заведен в стеклянную трубку 1. Для пополнения сосуда А служив трубка 5 с запорным устройством 6.

При ламинарном режиме движения жидкости по трубке 1 струйка раствора краски, истекающей из трубки 3, имеет вид четко вытянутой нити вдоль трубки 1.

По мере открытия крана 2 увеличивается скорость движения и режим движения переходит в турбулентный, при этом струйка приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке. При постепенном закрытии крана эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным.

Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической),которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.
Билет 11.

1. Число Маха и диапазон его изменения (с пояснениями).

Число Маха: M= W/a, где W- скорость потока, a- скорость звука.

M<1 – течение дозвуковое

M>1 – течение сверхзвуковое

W=0 T=T* → a=a*=√kRT* - скорость в неподвижной среде M=0

W=W_max T=0 → a=0 →M=
2. Преобразование полной энтальпии в кинетическую энергию потока. Максимальная скорость. Критическая скорость.

Для энергетически изолированного перевода газа из состояния покоя (W=0, i*, T*) в состояние движения с параметрами W, i, T необходимо израсходовать часть полной энтальпии в соответствии с уравнением: i* -i= W²/2. Отсюда получаем формулу для расчета скорости течения газа в точке любого потока по значениям i и i* в этой точке:



Максимальная скорость истечения (W_max). При энергетически изолированном течении скорость W_max будет получена тогда, когда полная энтальпия целиком будет превращена в кинетическую энергию, т.е. когда газ расширится до абсолютного вакуума T=0, p=0 и =0: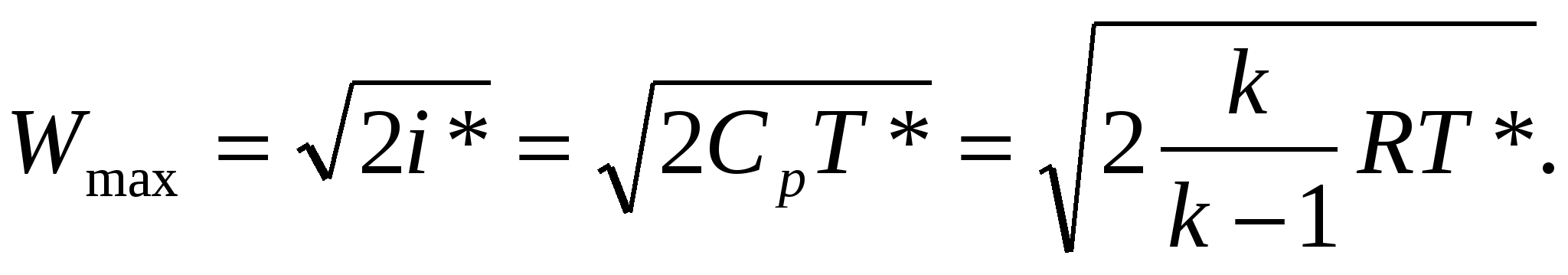



Критической называется скорость потока, равная местной скорости звука. При критическом (звуковом) течении все параметры потока называются критическими. Критическая скорость устанавливается при израсходовании на ускорение газа лишь определенной части полного теплосодержания:

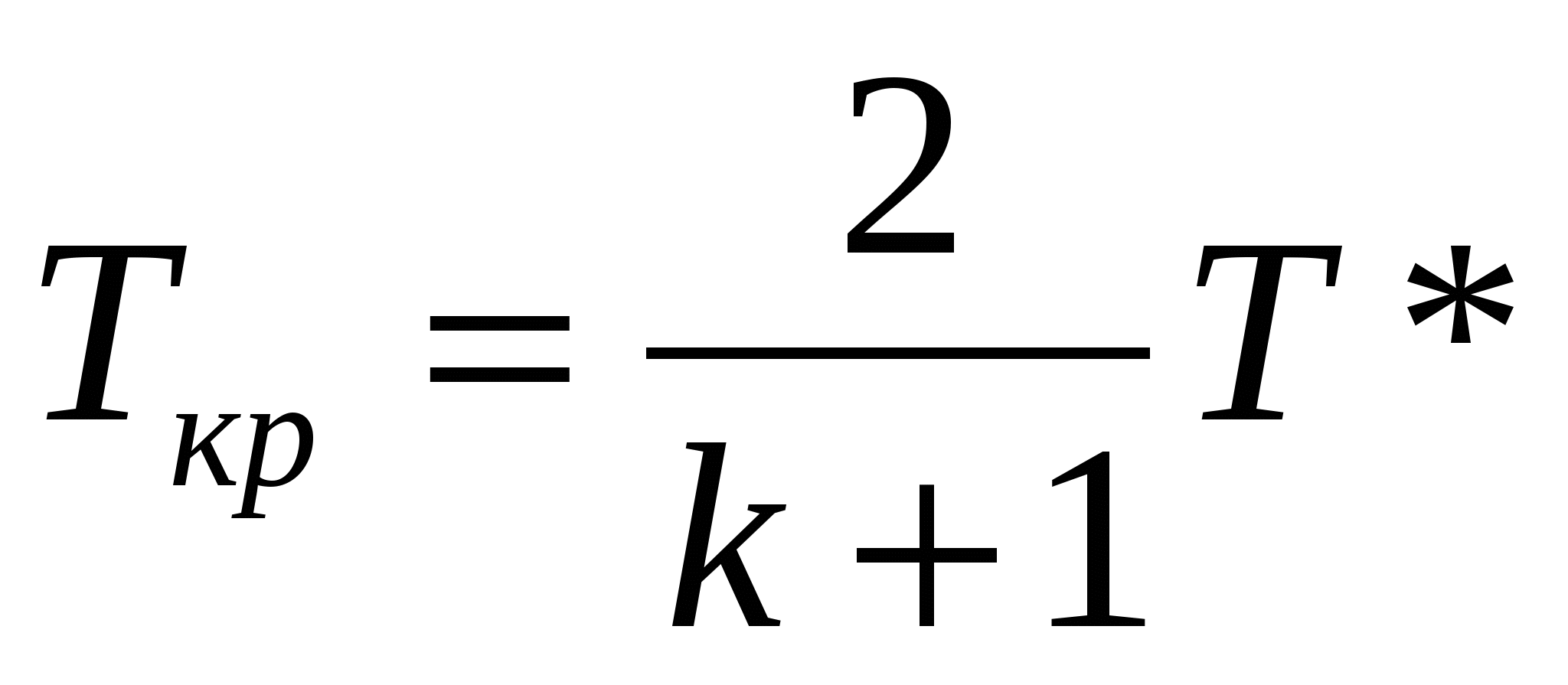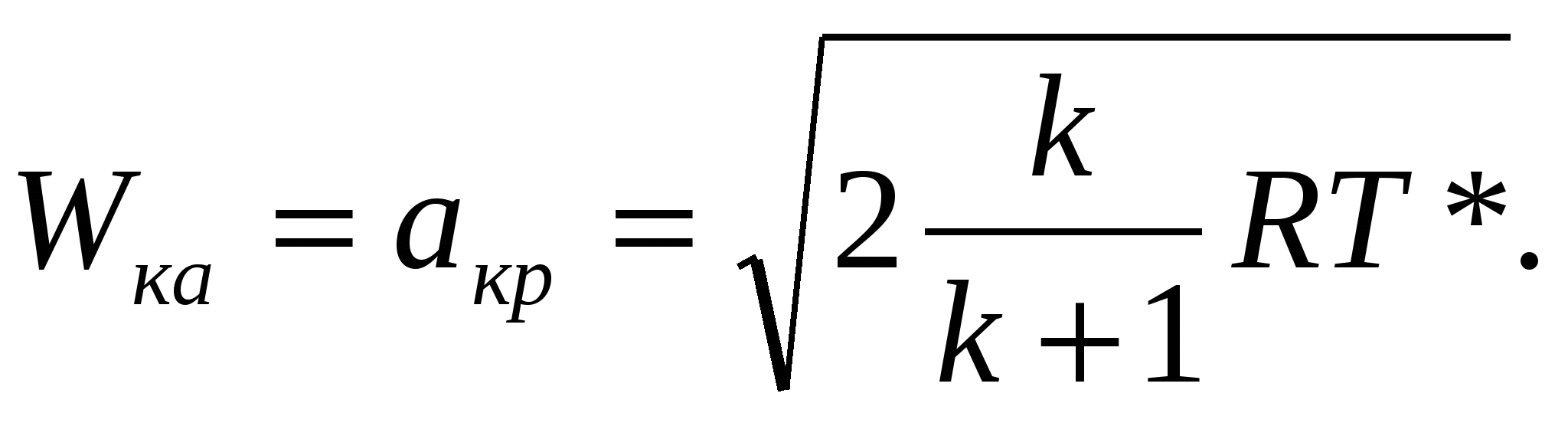Тогда критическая температура равна: , критическая скорость звука: 3. Основные понятия пограничного слоя.

Влияние вязкости сосредотачивается лишь в области потока непосредственно прилегающего к поверхности тела. Эта область имеет малую по сравнению с длиной тела протяженность по направлению к нормальной поверхности тела и большие поперечные градиенты скорости dW/dy>>0 и называется пограничным слоем. Вне пограничного слоя течение жидкости можно считать идеальным. Толщина пограничного слоя – это расстояние на котором достигается равенство W=W₀→. Принято считать, что =Y_W=0.99W0 или =Y_W=0.999W0.

В пограничном слое происходит потеря количества движения жидкости, что определяет сопротивление, которое твердая стенка оказывает на движение жидкости. Т.о. гидравлические потери сосредоточены в пограничном слое, а за его пределами отсутствуют. Предполагается, что из-за малой толщины пограничного слоя давление существующее в течении на внешней границы слоя передается без изменения: dp/dy =0.

Кроме пограничного слоя, в котором меняются скорость, различают температурный пограничный слой и диффузионный.
Билет 14.

1. Газодинамические функции параметров торможения: определение, диапазон и характер изменения. Критическое отношение давлений.

Газодинамическими функциями параметров торможения являются (λ), (λ), (λ).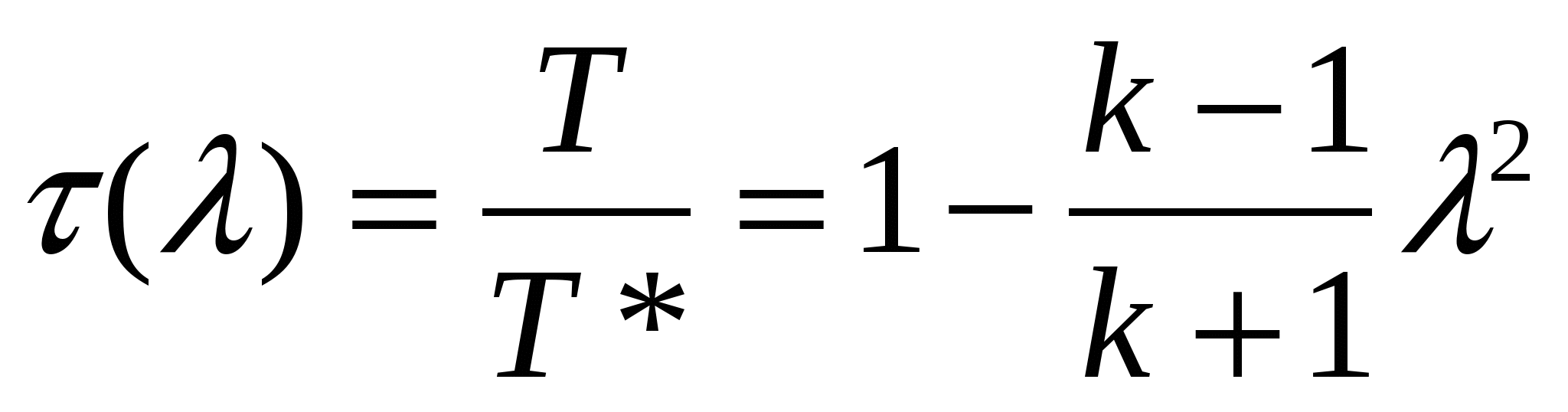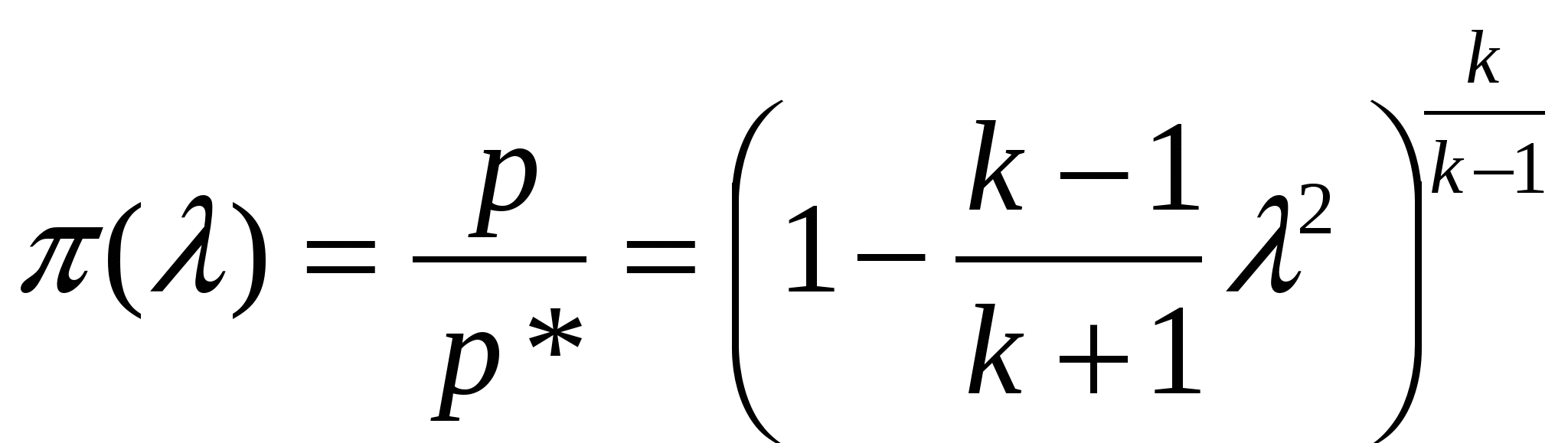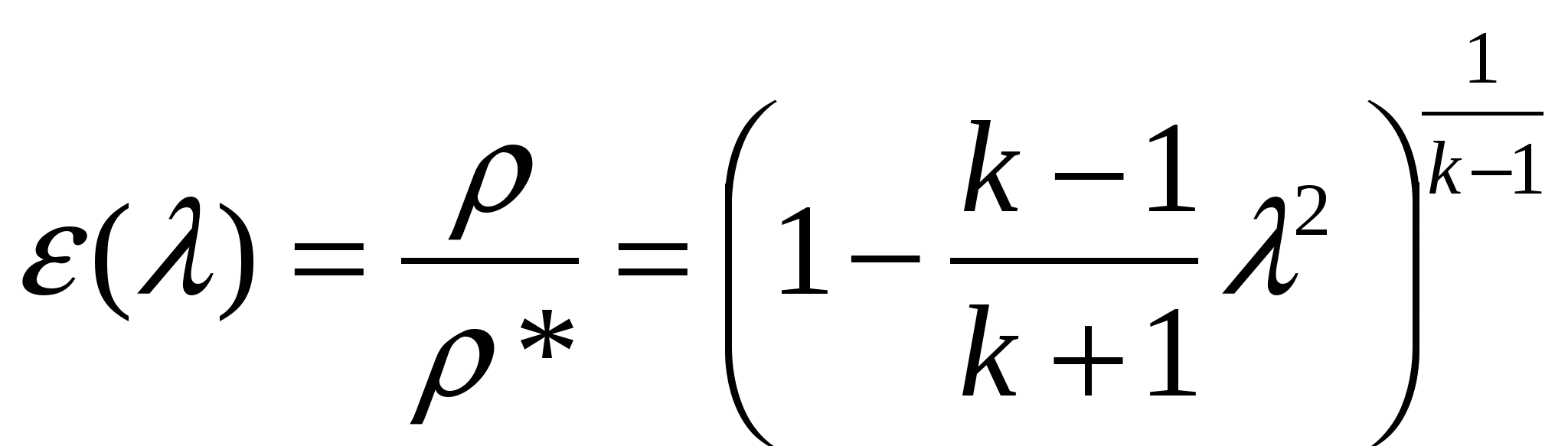



Связь между (λ), (λ), (λ) установим, поделив уравнение состояния для термодинамических параметров р=RT на уравнение состояния для параметров торможения р*=*RT*:

(λ) =  (λ) (λ)

Иногда удобно использовать функцию β(λ)=1/ (λ) =p*/p.

Величина β _кр(λ)=1/ (1) =p*/p_кр известна как минимальное отношение давлений в резервуаре и в выходном течение идеально суживающегося котла, в котром выходное сечение достигает максимальной скорости течение W=W_кр.

2. Сложные трубопроводы.

К сложным трубопроводам следует относить те трубопроводы, которые не подходят к категории простых трубопроводов, т.е к сложным трубопроводам следует отнести:

трубопроводы, собранные из труб разного диаметра (последовательное соедине­ние трубопроводов),

трубопроводы, имеющие разветвления: параллельное соединение трубопроводов, сети трубопроводов, трубопроводы с непрерывной раздачей жидкости.

Последовательное соединение трубопроводов. При последовательном соединении трубопроводов конец предыдущего просто­го трубопровода одновременно является началом следующего простого трубопрово­да. В сложном трубопроводе, состоящем из последовательно соединённых простых трубопроводов, последние в литературе на­зываются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопрово­де будут равны сумме потерь напора во всех отдельных его участках. , где - потери напора на- том участке трубопровода.

Таким образом, потери напора в трубопроводе, состоящем из последовательно со­единённых друг с другом участков равны квадрату расхода жидкости в трубопроводе ум­ноженному на сумму удельных сопротивлений всех участков.

Гидравлическая характеристика трубопровода состоящего из последовательно со­единённых участков представляет собой графическую сумму (по оси напоров) гидравли­ческих характеристик всех отдельных участков. На рисунке кривая 1 представляет гид­равлическую характеристику 1-го участка трубопровода, кривая 2 - гидравлическую ха­рактеристику 2-го участка, кривая 3 - сумму гидравлических характеристик обеих участ­ков.

Сложный трубопровод, состоящий из последовательно соединённых простых трубо­проводов можно свести к простому трубопроводу с одинаковым (эквивалентным) диамет­ром, при этом длины участков будут пересчитываться, чтобы сохранить реальные гидрав­лические сопротивления участков трубопровода. Так приведённая длина - того участка l_пр будет:.

Следует отметить, что величина скоростного напора также зависит от диаметра трубопровода, и при определении приведённой длины участка мы вносим некоторую ошибку, которая будет тем большей, чем больше разница в величинах фактического и эк­вивалентного диаметров. В таких случаях можно рекомендовать другой, более сложный способ.

Параллельное соединение трубопроводов. Схема прокладки параллельных трубо­проводов используется в тех случаях, когда на трассе магистрального трубопровода есть участки, где требуется уменьшить гидрав­лические сопротивления трубопровода (вы­сокие перевальные точки трубопровода) или при заложении трубопровода в трудно­ доступных местах (переход через реки и др.). При параллельном соединении трубо­проводов имеются две особые точки, называемые точками разветвления. В этих точках находятся концы параллельных ветвей трубопровода (точки А и В). Будем считать, что жидкость движется слева направо, тогда общий для всех ветвей напор в точке А будет больше напора в другой общей для всех ветвей трубопровода точке В (Н_А Н _к). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в еди­ный трубопровод. Каждая ветвь может иметь различные геометрические размеры: диа­метр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е. Q=∑Q_i .

Жидкость движется по всем ветвям при одинаковой разности напоров: H_ав = H_а +H_в> тогда расход жидкости по каждой ветви можно записать в виде: .

Поскольку ветвей в системе п,, а число неизвестных в системе уравнений будет п+1, включая напор, затрачиваемый на прохождение жидкости по всем ветвям H_ав, то в каче­стве дополнительного уравнения в системе будет использовано уравнение неразрывности: Q=∑Q_i.

При решении системы уравнений можно воспользоваться соотношением:

Для построения гидравлической характери­стики системы параллельных трубопроводов можно воспользоваться методом графического суммирования. Суммирование осуществляется по оси расходов Q. т.к.