3. Управление пограничным слоем.
Методы управления пограничным слоем для уменьшения или увеличения сопротивления тел и тепло-, массообмена между телами и потоками указывает теория пограничного слоя.
Две группы: 1. Искусственная ламинаризация пограничного слоя заключается в увеличении абсциссы Xкр точки перехода ламинарного пограничного слоя в турбулентный для уменьшения трения и тепло-, массообмена между поверхностью тела и потоком жидкости. Она заключается в уменьшении толщины пограничного слоя, интенсивности турбулентности набегающего потока, градиента давления и высоты гребешков шероховатости. Эффективными методами уменьшения толщины ламинарного ПС является охлаждение обтекаемой стенки (поверхности крыла топливом), удаление с поверхности тела наиболее заторможенных слоев ПЧ отсосом или сдувом ПС перед ожидаемой точкой перехода, а также уменьшение dp/dx>0 за счет применения ламинаризованных профилей, в которых диффузорная часть отнесена к корме.
2. Для увеличения трения, теплообмена и диффузию, следует турбулизировать пограничный слой. Отрыв ПС модно предотвратить, уменьшая dp/dx>0 и толщину ПС любым из разобранных выше способом, а также искусственно турбулизуя ЛПС перед точкой отрыва с помощь. Установки турбулизирующего ребра
Билет 20.
1. Траектория, линия тока, трубка тока.
Линия тока – это пространственная кривая, в каждой точке которой в данный момент времени вектор скорости направлен по касательной.
При установившемся движении линия тока совпадает с траекторией. Дифференциальное уравнение линии тока: dx/u = dy/ =dz/.
Если взять в жидкости произвольный замкнутый контур и ч/з все его точки провести линии тока, то образуется поверхность тока, называемая трубкой тока. Трубка тока непроницаема для частичек, движущихся по обе стороны от нее, т.к. во всех ее точках у частиц жидкости отсутствует нормальные составляющие скорости. Если контур охватывает бесконечно малую площадку, то трубка тока называется элементарной. Жидкость, движущуюся внутри такой трубки, называют элементарной струйкой или просто струйкой.
3. Истечение жидкости через отверстия и насадки (качественные причины формирования той или иной картины).
Одной из типичных задач гидравлики, которую можно назвать задачей прикладного
характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. При таком движении вся потенциальная энергия жидкости находящейся в ёмкости (резервуаре) в конечном итоге расходуется на кинетическую энергию струи, вытекающей в газообразную среду, находящуюся под атмосферным давлением или (в отдельных случаях) в жидкую среду при определённом давлении. Отверстие будет считаться малым, если его размеры несоизмеримо малы по сравнению с размером свободной поверхности в резервуаре и величиной напора. Стенка называется тонкой, если величиной гидравлических сопротивлений по длине канала в тонкой стенке можно пренебречь. В таком случае частицы жидкости со всех сторон по криволинейным траекториям движутся с некоторым ускорением к отверстию. Дойдя до отверстия, струя жидкости отрывается от стенки и испытывает преобразования уже за пределами отверстия
Н асадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадка полностью соответствовал размеру отверстия в тонкой стенке. Наличие такой направляющей трубки приве дет к увеличению расхода жидкости при прочих равных условиях. Причины увеличения следующие При асадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадка полностью соответствовал размеру отверстия в тонкой стенке. Наличие такой направляющей трубки приве дет к увеличению расхода жидкости при прочих равных условиях. Причины увеличения следующие При
отрыве струи от острой кромки отверстия струя попадает в канал насадка, а поскольку струя испытывает сжатие, то стенок насадка она касается на расстоянии от 1,0 до 1,5 его диаметра. Воздух, который первоначально находится в передней части насадка, вследствие неполного заполнения его жидкостью постепенно выносится вместе с потоком жидкости. Таким образом, в этой области образуется «мёртвая зона», давление в которой ниже,
чем давление в окружающей среде (при истечении в атмосферу в «мёртвой зоне» образуется вакуум). За счёт этих факторов увеличивается перепад давления между резервуаром и областью за внешней его стенкой и в насадке генерируется так называемый эффект подсасывания жидкости из резервуара. Однако наличие самого насадка увеличивает гидравлическое сопротивление для струи жидкости, т.к. в самом насадке появляются потери напора по длине трубки. Если трубка имеет ограниченную длину, то влияние подсасывающего эффекта с лихвой компенсирует дополнительные потери напора по длине. Практически эти эффекты (подсасывание и дополнительные сопротивления по длине) компенсируются при соотношении: / = 55 d. По этой причине длина насадков ограничивается / = (3 -5)d . По месту расположения насадки принято делить на внешние и внутренние насадки. Когда насадок монтируется с внешней стороны резервуара (внешний насадок), то он оказывается более технологичным, что придаёт ему преимущество перед внутренними насадками. По форме исполнения насадки подразделяются на цилиндрические и конические, а по форме входа в насадок выделяют ещё коноидальные насадки, вход жидкости в которые выполнен по форме струи.
Билет 26.
1. Среднерасходная скорость. Коэффициент Кориолиса.
Расходом жидкости называется количество жидкости, проходящей через данное живое сечение потока в единицу времени.
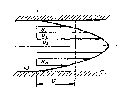 На рис. представлен график (эпюра) распределения действительных скоростей в точках живого сечения потока, из которого видно, что скорости по сечению распределяются неравномерно. При действительных скоростях через живое сечение проходит определенный расход Q. Можно найти некоторую постоянную для всех точек сечения фиктивную скорость, при которой через данное сечение проходил бы тот же самый расход, что и при действительных скоростях движения жидкости. Эта скорость vбудет средней из действительных скоростей. На рис. представлен график (эпюра) распределения действительных скоростей в точках живого сечения потока, из которого видно, что скорости по сечению распределяются неравномерно. При действительных скоростях через живое сечение проходит определенный расход Q. Можно найти некоторую постоянную для всех точек сечения фиктивную скорость, при которой через данное сечение проходил бы тот же самый расход, что и при действительных скоростях движения жидкости. Эта скорость vбудет средней из действительных скоростей.
Итак, средней скоростью потока в данном сечении vназывается такая одинаковая для всех точек живого сечения скорость движения жидкости, при которой через это живое сечение проходит тот же расход Q, что и при действительных скоростях движения жидкости и.  , Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией , Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией 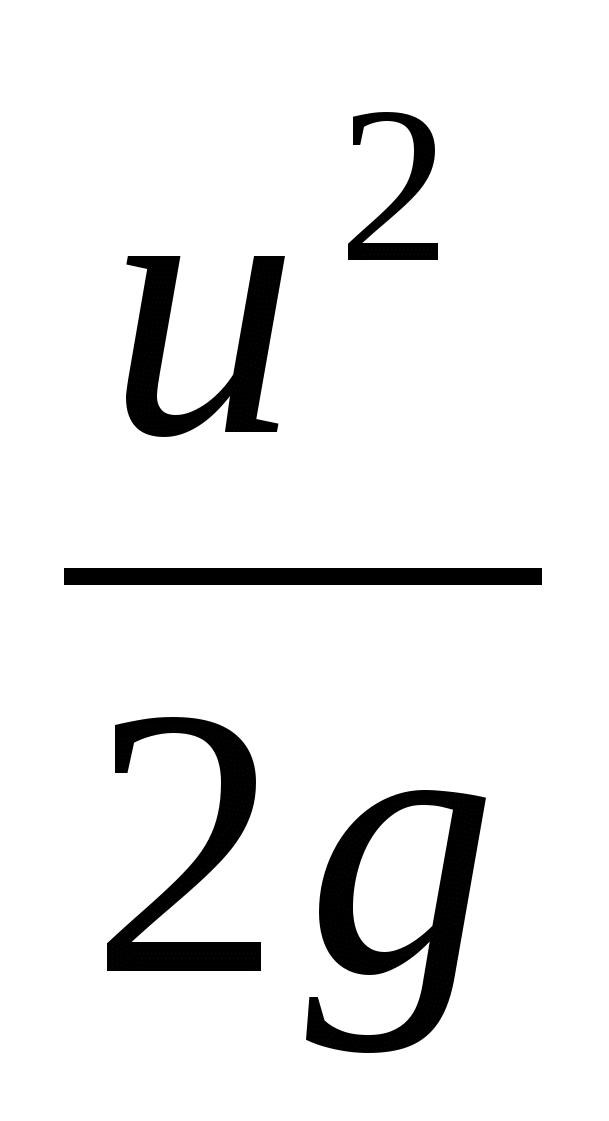 . Эта величина различна для разных струек, образующих поток. . Эта величина различна для разных струек, образующих поток.
Определим среднее значение этой величины в сечении потока. Для этого действительные скорости элементарных струек u1, u2, ..., ипзаменим средней скоростью потока v;тогда среднее значение удельной кинетической энергии потока в данном сечении равно
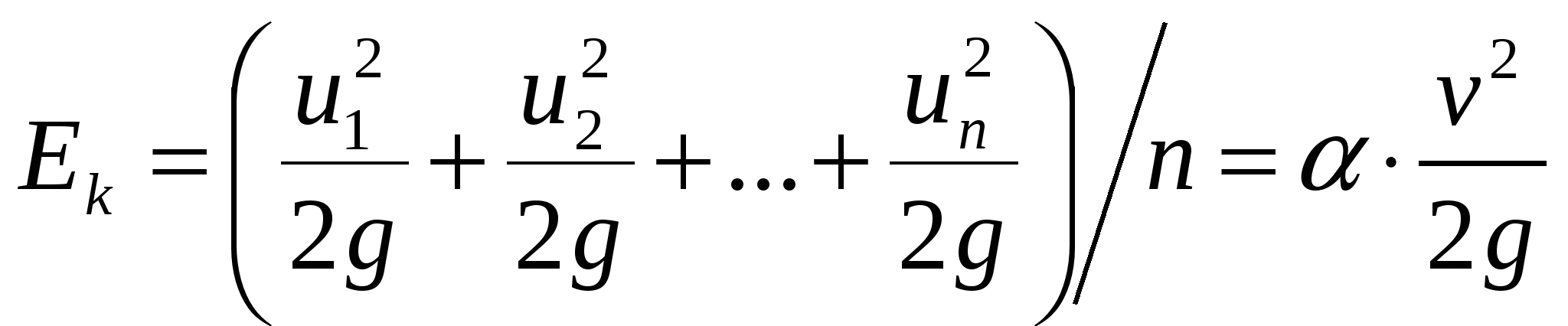
Здесь – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии).
Безразмерный коэффициент представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Если эпюра скоростей в сечении потока близка к прямоугольной, т.е. скорости в разных точках близки к средней, то коэффициент Кориолиса близок к единице. Если же скорости в сечении значительно различаются между собой, то и коэффициент оказывается значительно больше единицы.
На основе обработки многочисленных данных, полученных на реках и каналах, установлено, что для больших открытых потоков  . При равномерном движении в трубах и каналах практически . При равномерном движении в трубах и каналах практически 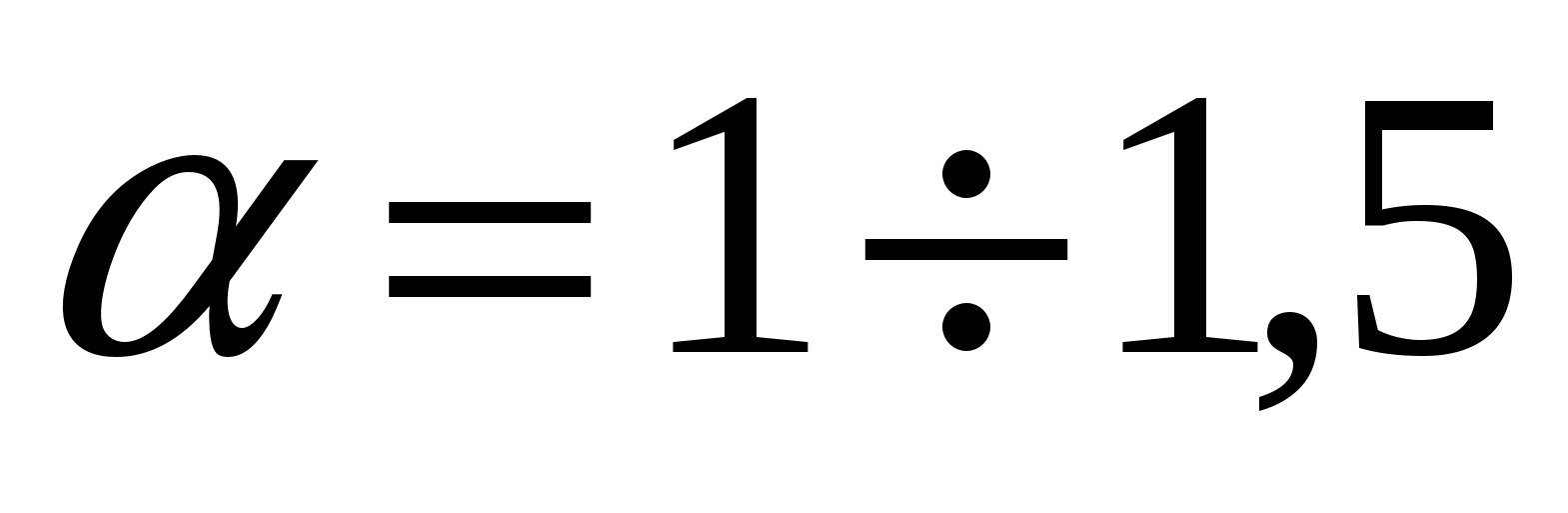 . .
В дальнейшем, за исключением особо оговоренных случаев, для упрощения расчетов будем принимать 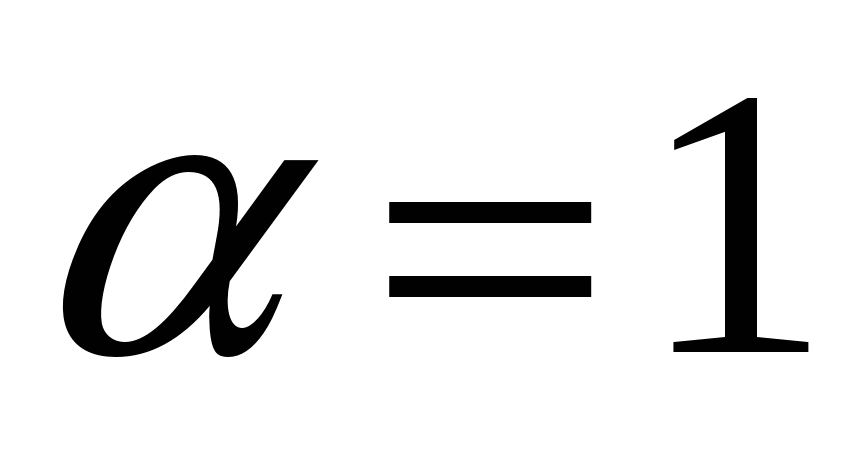 . Однако следует помнить, что в некоторых случаях при неравномерном распределении скоростей значения могут быть значительно больше 1 (2 и более). . Однако следует помнить, что в некоторых случаях при неравномерном распределении скоростей значения могут быть значительно больше 1 (2 и более).
Мгновенные скорости пульсируют около своего осредненного значения, которое за достаточно длительный промежуток времени остается постоянным; это значение и называется осредненной скоростью.
3. Кавитация. Влияние кавитации на работу насосов.
Если при входе в рабочее колесо насоса абсолютное давление окажется меньшим или равным упругости паров перекачиваемой жидкости при данной температуре, то жидкость начинает вскипать, происходит разрыв потока и подача прекращается.
При длительной работе насоса в таких условиях разрушается рабочее колесо. Явления, происходящие в насосе при вскипании жидкости, называются кавитацией. При этом из жидкости выделяются пары и растворенные газы в том месте, где давление равно или меньше давления насыщенных паров. Пузырьки пара и газов, увеличенные потоком в область повышенного давления, резко конденсируются с уменьшением объема в микроскопических зонах; это явление, подобное взрывам мельчайших бомб, приводит к механическим повреждениям лопаток колеса и их разрушению.
Кавитация может происходить не только в рабочем колесе, но и в направляющем аппарате, и в спиральном корпусе. Эти явления сопровождаются потрескиванием, шумом и вибрацией насоса. При кавитации резко падает к. п. д. насоса, производительность и напор. Особенно сильно при кавитации разрушаются чугун и углеродистая сталь, наиболее устойчивы бронза и нержавеющая сталь. Поэтому в последнее время для изготовления насосов применяют высококачественные материалы и защитные покрытия (наплавка твердых сплавов, поверхностная закалка, металлизация в холодном состоянии), что повышает надежность работы насосов.
Во избежание явления кавитации насос следует располагать как можно ниже.
Кавитационный запас уровня определяют по уравнению 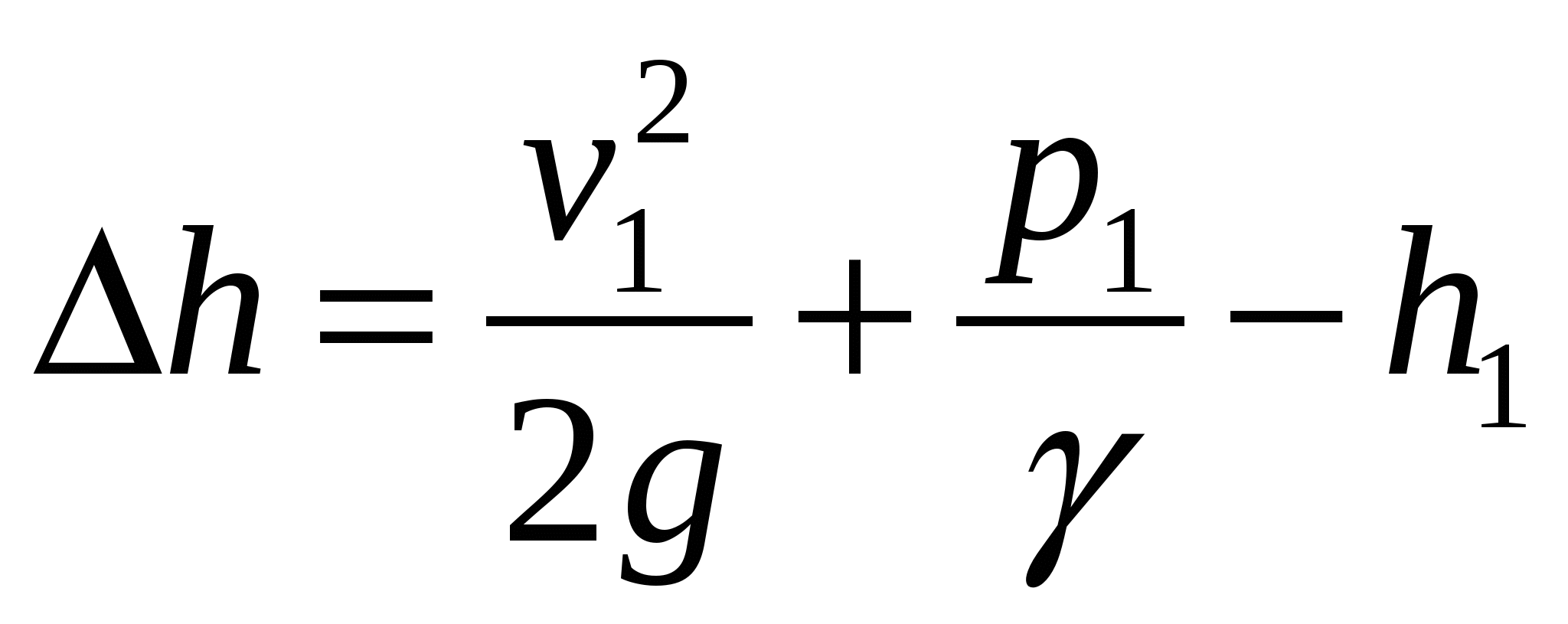 . .
Билет 29.
2. Свойства напряжения поверхностных сил. Давление и его свойства.
Выделим в движущейся жидкости элементарный прямоугольный тетраэдр. Составим векторное уравнение движения жидкого тетраэдра, выражающее второй закон Ньютона:
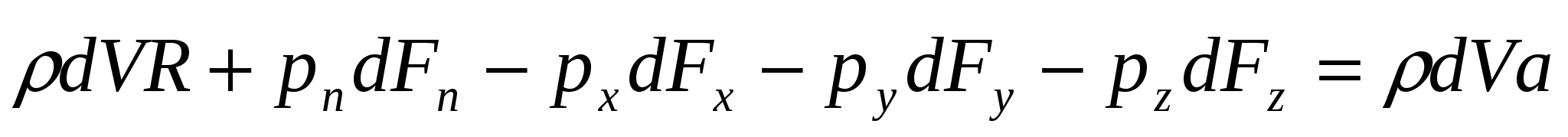
Подставим в это уравнение: 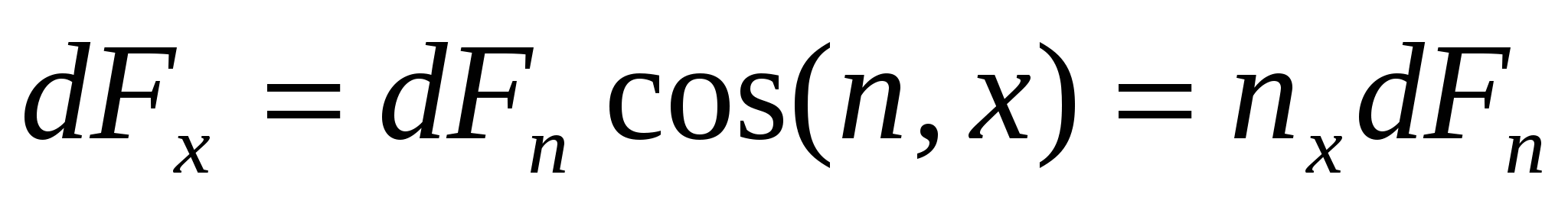 , (xyz). Учтем. Что члены dVR и dVa имеют высший по сравнению с другими порядок малости, и ими можно пренебречь. В результате получим: , (xyz). Учтем. Что члены dVR и dVa имеют высший по сравнению с другими порядок малости, и ими можно пренебречь. В результате получим: 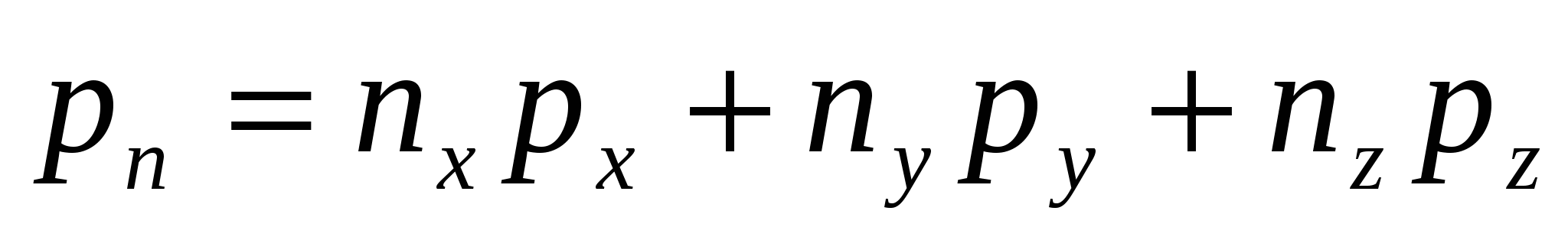 (1). С другой стороны, каждый из векторов (1). С другой стороны, каждый из векторов 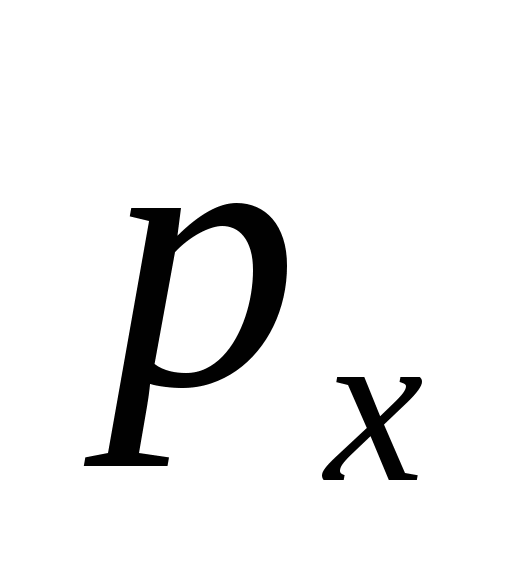 (xyz) может быть представлен тремя составляющими, действующими вдоль координатных осей в виде: (xyz) может быть представлен тремя составляющими, действующими вдоль координатных осей в виде:   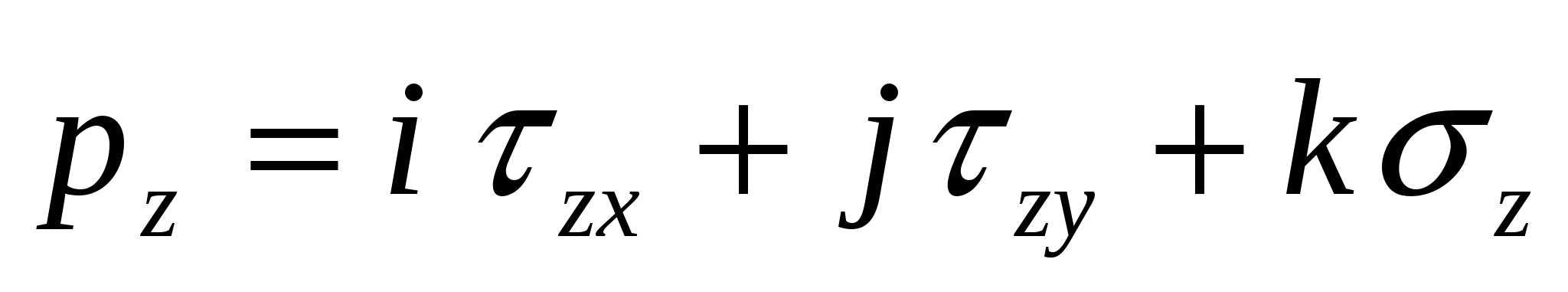 (2). -нормальное напряжение, - касательное напряжение (2). -нормальное напряжение, - касательное напряжение
Спроецируем (1) на координатные оси, учитывая (2). Получим: 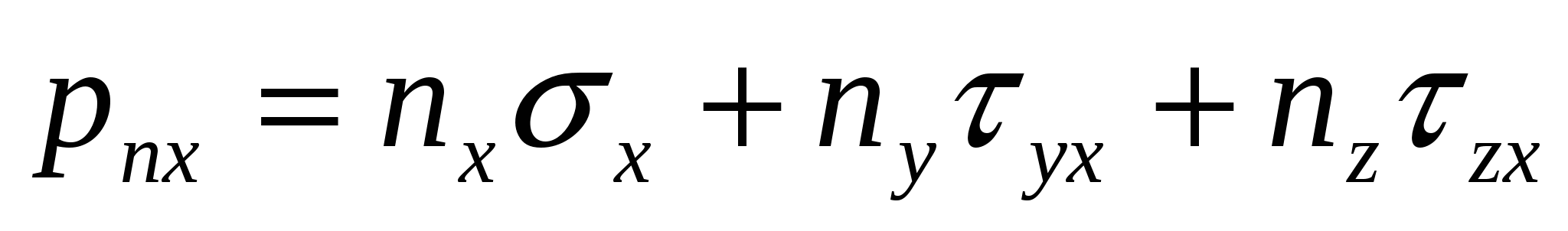 (xyz). (xyz).
По закону парности касательных напряжений: xy = yx…
Получим: pnx = nx x (xyz).
С другой стороны pnx =pn i = pn cos (n,x) = pn nx (xyz).
Полученный результат справедлив и для вязкой жидкости, но находящейся в покое, т.к. вязкость проявляется только при относительных перемещениях слоев жидкости.
Жидкости и газы в силу своего строения не могут воспринимать растягивающие напряжения. Поэтому нормальные напряжения должны быть сжимающими. Такое сжимающее нормальное напряжение называется давлением и обозначается p: p =-pn= -x= -y= -z. (3)
Сле-но, давление всегда направлено по внутренней нормали к поверхности жидкости. Это первое свойство давления.
Перепишем (3) p =px= py= pz, где px= -x, py= -y, pz= -z. Давление – величина положительная и в любой точке идеальной или покоящейся вязкой жидкости одинаковая по всем направлениям, т.е. не зависит от ориентации площадки в пространстве. Это второе свойство давления. Но давление неодинаково в различных точках пространства и может изменяться во времени.
3. при течении несжимаемой жидкости в трубах в общем случае …
Было установлено, что при больших числах Рейнольдса и высокой шероховатости коэффициент гидравлического трения 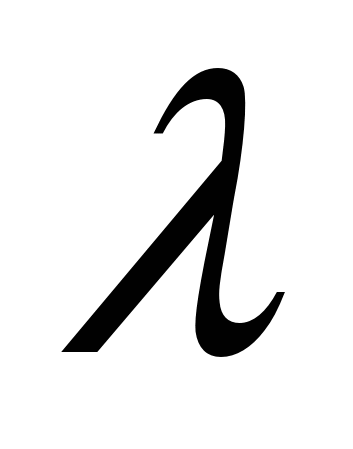 в трубах совсем не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости (в этих условиях трубы и русла называют вполне шероховатыми). Трубы же, в которых коэффициент в трубах совсем не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости (в этих условиях трубы и русла называют вполне шероховатыми). Трубы же, в которых коэффициент 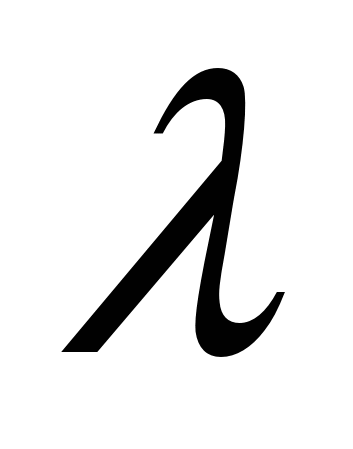 зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Reи k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Reи k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых 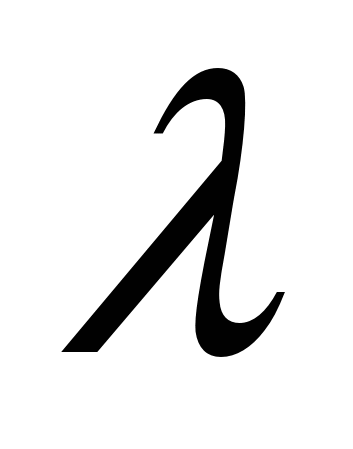 зависит и от числа Рейнольдса и от относительной шероховатости, называются переходной областью. Это объясняется тем, что при малых числах Рейнольдса вблизи стенок сохраняется сравнительно толстый ламинарный слой, и выступы шероховатости обтекаются жидкостью без образования и отрыва вихрей. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление, и зависимость зависит и от числа Рейнольдса и от относительной шероховатости, называются переходной областью. Это объясняется тем, что при малых числах Рейнольдса вблизи стенок сохраняется сравнительно толстый ламинарный слой, и выступы шероховатости обтекаются жидкостью без образования и отрыва вихрей. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление, и зависимость 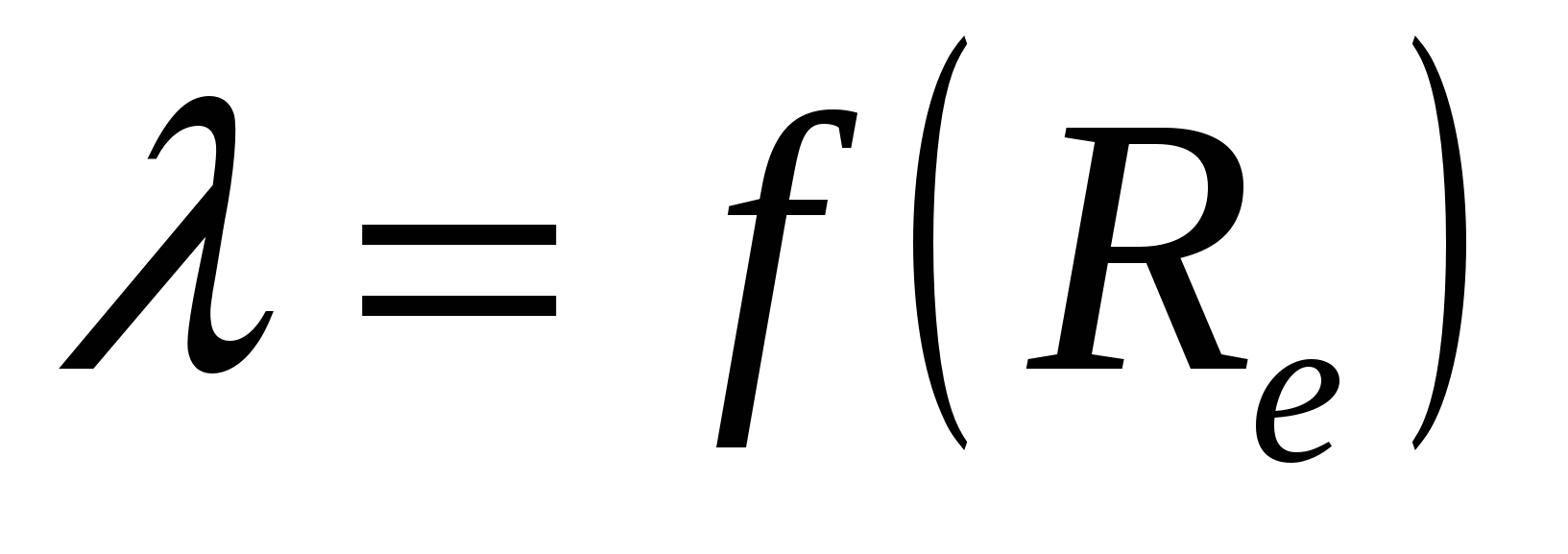 выражается в логарифмических координатах прямой. выражается в логарифмических координатах прямой.
=(h/r, Re) – переходная область
(Re) – трубы вполне шероховатые
Билет 34.
1. Поле течения жидкости.
Для описание области течения жидкости необходимо знать следующие параметры: скорость, плотность, давление, температуру.
u=u(x, y, z, t); υ=υ(x, y, z, t); ω=ω(x, y, z, t)
=(x, y, z, t)
p=p(x, y, z, t)
T=T(x, y, z, t)
1. Принцип вывода дифференциальных уравнений Рейнольдса осредненного турбулентного движения. Особенности уравнений Рейнольдса..
Влияние пульсации скорости на осредненное турбулентное течение проявляется как бы в увеличении вязкости осредненного движения по сравнению с молекулярной вязкостью. Это дополнительная или кажущаяся вязкость или кажущиеся турбулентные напряжения – является основными понятиями всх современных теорий турбулентности. Термин «кажущаяся» означает инерционный характер турбулентных напряжений.
Дифференциальные уравнения осредненного турбулентного движения, предложенные Рейнольдсом, получаются подстановкой в уравнение неразрывности Навье - Стокса и др. уравнения сохранения истинных параметров турбулентного движения согласно зависимостям  (u, v, p, , ) с последующим осреднением по определенным правилам. (u, v, p, , ) с последующим осреднением по определенным правилам.
Для установленного течения несжимаемой жидкости при отсутствии массовых сил эти уравнения можно привести к виду уравнений движения в напряжениях с той разницей, что в них:
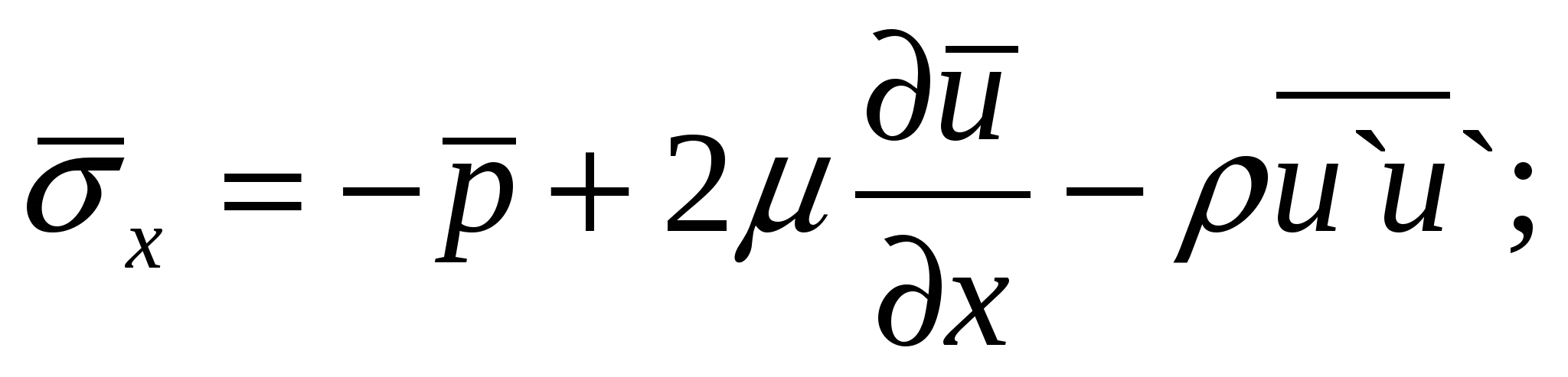  В выражении появляется дополнительное слагаемое, обусловленное турбулентной вязкостью. В выражении появляется дополнительное слагаемое, обусловленное турбулентной вязкостью.
|
 Скачать 0.89 Mb.
Скачать 0.89 Mb.