Конспект урока по алгебре и началам анализа на тему _Площадь кри. Площадь криволинейной трапеции
 Скачать 418 Kb.
|
|
Тема: «Площадь криволинейной трапеции». Цели и задачи: Обучающие: Обобщение знаний обучающихся о первообразной. Познакомить с понятием криволинейной трапеции; научить вычислять площадь криволинейной трапеции как приращение первообразной. Сформировать навыки планирования ответа, умение считать и писать в быстром темпе, навыки самоконтроля Развивающие: Развивать умение систематизировать и применять полученные знания Развивать логическое мышление и внимание. Воспитательные: Воспитывать сознательную дисциплину и нормы поведения. Воспитывать математическую культуру Формировать потребности в приобретении знаний. Тип урока: изучение нового материала Наглядность и оборудование: учебник «Алгебра и начала анализа. 10-11 класс» , телевизор, компьютер, презентация, демонстрационная таблица, запись на доске, тетрадь, карандаш, ручка, линейка. План урока:
Ход урока: I.Организационный момент: (Сообщение темы и целей урока.) II. Устная работа. Один обучающийся на компьютере показывается геометрический смысл свойства первообразной для заданной функции у=х3 Одновременно у доски работают индивидуально двое обучающихся по карточкам, содержащим задания разной степени трудности (его решение после выполнения проверяет группа). Задание №1 Оценка «5» Найдите для функции f одну из первообразных: а) f(x) =  ;б) f(x) = - cos (5x-3); в) f(x) = sin  2x; г) f(x) =  .Задание №2 Оценка «4» Найдите общий вид первообразных для функции f: а) f(x) = 2 cos x – 3 sin x; б) f(x) = 8x  - 3x - 4;в) f(x) =  ; г) f(x) =  .Вопросы обучающимся группы: 1)Что называется первообразной? 2) Основное свойство первообразной? 3) Устные задания с помощью компьютерной презентации. III. Изучение нового материала. Практическая работа (один обучающийся выполняет на доске цветным мелом, остальные - в тетрадях) Построить прямоугольную систему координат; На оси абсцисс отложить отрезок [a ; b]; На заданном отрезке построить график неотрицательной, непрерывной функции; Построить прямые x=a и x=b; Заштриховать фигуру, ограниченную линиями разного цвета. Сообщить, что заштрихованная фигура называется криволинейной трапецией Предложить обучающимся сформулировать самим определение криволинейной трапеции Записать определение криволинейной трапеции в тетрадь Определение: Фигуру, ограниченную снизу отрезком [a:b] оси Ох, сверху – графиком непрерывной неотрицательной функции y=f(x), с боков – отрезками прямых х=а и х=b (Отрезок [a:b] называется основанием криволинейной трапеции) О 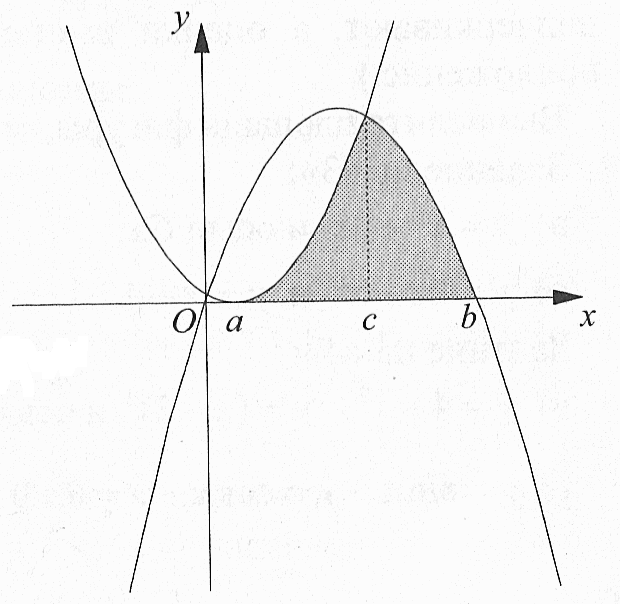  братить внимание на экран телевизора и предложить на изображенных рисунках найти фигуры, которые не являются криволинейными трапециями, объяснить свой ответ.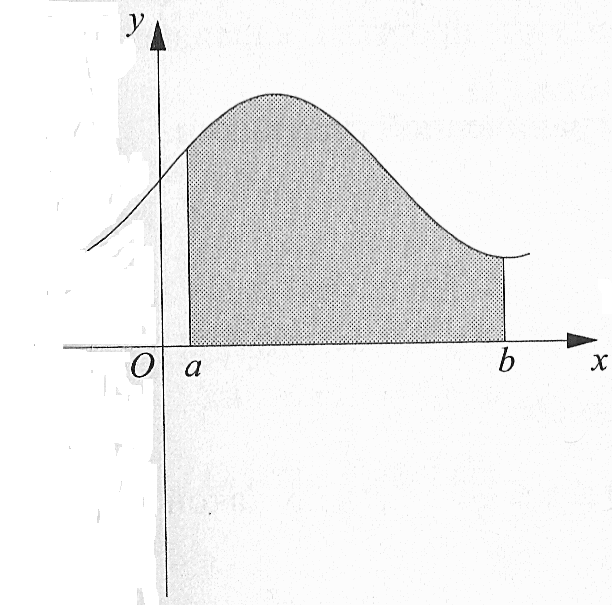  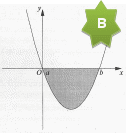 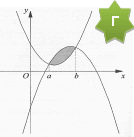 Преподаватель Каждая криволинейная трапеция имеет свою площадь. Для вычисления площадей криволинейной трапеции применяется следующая теорема: Если f – непрерывная и неотрицательная на отрезке [a;b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a;b], т.е. S = F(b) — F(a) (Записать формулировку теоремы в тетрадь стр. 186, разбор доказательства дома) IV. Закрепление изученного материала. Показ слайда Пример: Найдите площадь криволинейной трапеции, ограниченной линиями: а) y=x ; y=0; a=1; b=2 (разбор с преподавателем)б) y=x ; y=0; a=0; b=2 (один обучающийся выполняет на доске)в) y=x ; y=0; a= -2; b= -1 (самостоятельно выполняют все)Работа с учебным пособием Работа на доске: №353(б); №354(а). Самостоятельная работа: №354(б) V. Итог урока. Вопросы: Какую фигуру называют криволинейной трапецией? Назвать формулу для вычисления площади криволинейной трапеции? VI. Домашнее задание. Пункт 29, страница 186-187 (разобрать доказательство теоремы о площади криволинейной трапеции) , решить №353 (в,г), №354 (в,г), повторить графики элементарных функций Приложения.(Решения) Задание 1 Оценка «5» а) f(x) = F(x) =  = 0,25  б) f(x) = - cos (5x-3)  F(x) = - 0,2 sin (5x-3) в) f(x) = sin 2xF(x) = -   = - cos 2xг) f(x) = = (8x-3) F(x) =   = -  Задание 2 Оценка «4» а) f(x) = 2 cos x – 3 sin x F(x) = 2 sin x + 3 cos x + C б) f(x) = 8x - 3x - 4F(x) =  -  - 4x +CF(x) = x  - x - 4x + Cв) f(x) = F(x) = 3tg x +C с) f(x) = F(x) = 12  + CЗадание 5 На рис. б), в), г), фигуры не являются криволинейными трапециями, так как фигуры на рис. б), и г) ограничены графиками двух функции а фигура на рисунке в) расположена ниже оси Ох. Закрепление нового материала Пример а) Для функции f(x) = x одной из первообразных является F(x) =  . Следовательно,S = F (2) –F (1) =  Ответ:  б) S = F(2) - F(0) =  - 0 =  Ответ: в) S = F(-1) – F(-2) = -  + = Ответ: Задание №353 Для функции y= cos x одной из первообразных является F(x) = sin x Следовательно, S = F(  ) – F(0) = sin - sin 0 = 1Ответ: 1 Задание № 354 а) Для функции у = x + 1 одной из первообразных является F(x) =  Следовательно, S = F(2) – F(0) =  + 2 - Ответ: 6 б) Для функции y = 1 + 2 sin x одной из первообразных является F(x) = x - 2 cos x Следовательно, S = F ( ) - F(0) =  - 2 cos - 0 + 2 cos 0 = +2 Ответ: + 2 |