Тема Основные понятия и величины в гидравлике Предмет и методы гидравлики, основные характеристики жидкостей
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
ГИДРАВЛИКА (ускоренный курс) ТЕОРЕТИЧЕСКИЕ И РАСЧЕТНО-ПРАКТИЧЕСКИЕ МАТЕРИАЛЫ Тема 1. Основные понятия и величины в гидравлике Предмет и методы гидравлики, основные характеристики жидкостей Гидравлика (техническая гидромеханика) изучает движение (течение) и равновесие жидкостей под воздействием внешних сил, а также взаимодействие потоков жидкостей со стенками каналов и трубопроводов. Основными научными и практическими методами решения задач в гидравлике являются: - аналитические (теоретические), базирующиеся на различных физических моделях жидкостей и на математическом аппарате дифференциального и интегрального исчислений; - эмпирические (опытно-экспериментальные), в которых используются результаты опытов и основные положения теории подобия и размерностей. Объектом изучения в гидравлике являются жидкости – сплошные среды, состоящие из огромного числа (  1025) легкоподвижных частиц и обладающие свойством текучести. В каналах и трубах они легко перемещаются под действием разности уровней или давлений, при этом, основным качеством их является сплошность, т.е. способность целиком заполнять объем и равномерно распределяться в нем (так наз. Гипотеза сплошности). На этом допущении и основано применение дифференциального и интегрального исчисления при исследовании гидравлических процессов. 1025) легкоподвижных частиц и обладающие свойством текучести. В каналах и трубах они легко перемещаются под действием разности уровней или давлений, при этом, основным качеством их является сплошность, т.е. способность целиком заполнять объем и равномерно распределяться в нем (так наз. Гипотеза сплошности). На этом допущении и основано применение дифференциального и интегрального исчисления при исследовании гидравлических процессов.Исходной механической моделью жидкостей является так наз. идеальная жидкость, т.е. абсолютно текучая, несжимаемая (с постоянной плотностью) и теплопроводная (с неизменной температурой) жидкость. Реальные жидкости (вода, нефть и др.) могут существенно отличаться от этой модели из-за некоторых особых свойств: сжимаемости, температурного расширения, вязкости. Сжимаемость. Это свойство жидкости изменять объем и плотность под воздействием внешней силы (давления). Если на объем жидкости Vo(рис.1.1) будет давить внешняя сила F, приложенная к поршню, то это вызовет смещение поршня и уменьшение объема на величину ΔV. 2 Показателем сжимаемости является коэффициент объемного сжатия βv, определяемый как относительное уменьшение объема на единицу увеличения давления : 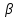 V = V = 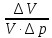 , Па – 1 , (1.1) , Па – 1 , (1.1)где ΔV– уменьшение начального объема Vo, Δр – увеличение давления из-за действия силы F, равное: Δр = F/Sп (Sп – площадь поршня).  F F    Vo Рис. 1.1. Определение коэффициента объемного сжатия    ΔV Плотность жидкости при сжатии увеличивается: ΔV Плотность жидкости при сжатии увеличивается:  Sп Δρ = ρ - ρо = т / (Vo– ΔV) (1.2) Sп Δρ = ρ - ρо = т / (Vo– ΔV) (1.2)  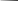 Пример 1.1. При гидравлических испытаниях водовода Пример 1.1. При гидравлических испытаниях водовода длиной L = 1000 м, диаметром d = 300 мм в трубопроводе создается избыточное давление Δр = 2 МПа путем закачки в уже заполненную водой трубу дополнительного объема жидкости ΔV. Коэффициент сжатия для воды βv = 2∙10-9 Па. Определить необходимый объем ΔV. Расчет: ΔV = βvVoΔp ; Vo=( πd2/4)L = 70,65 м3; отсюда ΔV = 0,282 м3. Температурное расширение. Оно происходит при нагреве жидкости на величину Δt = t – to, где to– ее начальная температура. Характеристикой этого свойства является коэффициент температурногорасширения βt, равный βt= 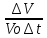 , , 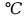 -1, (1.3) -1, (1.3)Пример 1.2. При нагреве воды в системах отопления зданий объем ее увеличивается, и прирост объема сбрасывается в так наз. расширительный бак, располагаемый обычно в верхней части трубопроводной системы. Необходимый минимальный объем бака находят по ф. (1.3). Расчет: Пусть дано Vo= 0,55 м3, Δt = 50o – 25o= 25oС. Тогда, взяв из справочника значение для воды βt= 0,0006 оС-1, получим VРБ = ΔV = βtVoΔt= 0,0083 м3. Плотность жидкости при нагревании уменьшается на величину Δρ = ρо – ρ = т/(Vo+ ΔV). При охлаждении жидкости происходит обратный процесс – уменьшения объема и увеличения плотности. 3 Гидростатическое давление. При сжатии жидкости внутри ее возникает напряжение (удельная сила), называемое гидростатическим давлением; оно равно р = F/ S, Н/м2 = Па. Давление обладает двумя важными свойствами: По всему объему жидкости (замкнутому) оно распространяется одинаково, т.е. действует на все частицы жидкости в объеме; Давление всегда направлено по нормали (перпендикулярно) к поверхности воздействия, например, к ограничивающим стенкам сосуда. Первое свойство является следствием сплошности жидкостей, оно лежит в основе закона Паскаля и широко используется в технике (в гидромеханизмах и устройствах, гидроприводах и т. д). Второе используется при расчетах силы давления на твердые стенки и поверхности. Пример 1.3. Гидравлический подъемник (рис. 1.2) состоит из двух гидроцилиндров – большого и малого диаметров, под которыми находится жидкость. При действии силы F1 на малый поршень, создаваемое давление р передается по всему жидкому объему и воздействует на большой поршень, который, в свою очередь, и создает выходное усилие F2, равное    Fo F1 F2 = F1 (S2 /S1). Fo F1 F2 = F1 (S2 /S1).           O F2    a b            dD Рис. 1.2. Схема гидроподъемника  Расчет. Даны: размеры цилиндров d = 100 мм, D = 500 мм, длина плеч рычага а = 400 мм, b = 100 мм, начальное усилие Fo= 10 H. Определить усилие F2 на выходном поршне. Сила, развиваемая этим поршнем, равна F2 = Fo (  )2 = 1250 H. )2 = 1250 H.Здесь сила F1 = Fo[(a + b) / b] = 10 [(0,4 + 0,1) /0,1] = 50 H, сила F2 = =F1(D/d)2 = 50(500/100)2 = 1250 H. 4 Единицы и приборы для измерения давления Основной единицей измерения давления является Паскаль, равный 1 Па = 1Н / 1 м2. На практике используются более крупные единицы: 1 кПа = 103 Па и 1 МПа = 106 Па. Кроме того, в технике и быту широко распространено применение некоторых специфических единиц, прежде всего, 1 бар = 1 атм ≈ 105 Па = 100 кПа = 0,1 МПа. Используются также некоторые единицы измерения, возникшие исторически из способов и приборов измерения. Пьезометр. Это прибор, с помощью которого определяют давление по высоте столба жидкости (рис.1.3). Если конец трубки открыт и сообщается с атмосферой, то прибор измеряет избыточное давление, т.е. внутри бака давление сверх атмосферного и его величина равна  ризб = ρghp(1.4).    рр Пример 1.4. hp Пусть высота столба жидкости (воды) в pизб         трубке пьезометра равна hp= 2,5 м, тогда давление над поверхностью жидкости в резервуаре будет ризб = 1000∙9,8∙2,5 = 24,5 кПа. То-есть, 1 бар ≈ 10 м. вод. столба. Рис. 1.3. Схема пьезометра Вакууметр. Аналогичный принцип измерения используется в приборах вакууметрах, определяющих недостаток до атмосферного давления (вакуум) в системах с пониженным давлением (рис. 1.4).              Пример 1.5. Чашечный вакууметр заполняется жидкостью, на поверхность которой действует атмосферное дав- рвнутр ление; давление внутри емкости ниже атмосфер- ного, т.е. вакуум равен рвак = ратм - рвнутр = ρghвак (1.5). hвак Рис.1.4. Схема вакууметра ратм 5              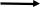   Дифманометр. Для измерения разности давлений между двумя точками применяется дифференциальный жидкостный манометр, чаще всего, заполненный ртутью (рис. 1.5), поэтому единицей измерения являются «миллиметры ртутного столба» (мм рт. ст.). Установим связь этой единицы с рассмотренными ранее, рассмотрев следующий пример. Дифманометр. Для измерения разности давлений между двумя точками применяется дифференциальный жидкостный манометр, чаще всего, заполненный ртутью (рис. 1.5), поэтому единицей измерения являются «миллиметры ртутного столба» (мм рт. ст.). Установим связь этой единицы с рассмотренными ранее, рассмотрев следующий пример.  р1 р2 Δhрт Рис. 1.5. Схема ртутного дифманометра  ρрт Дифманометром измеряется разность давлений, создаваемую клапаном, Δр = р1 – р2 = (ρрт – ρ)gΔhрт. (1.6) Пусть перепад на дифманометре равен Δhрт = 360 мм; тогда разность давлений будет Δр = (13600 – 1000)∙9,8∙0,360 = 44,45 кПа. Отсюда связь единиц измерения давления: 1 бар = 760 мм рт. ст. Итак, все основные единицы измерения давления можно объединить в следующую систему: 1 бар ≈ 1 атм = 10 м. вод ст. = 760 мм рт. ст. = 105 Па = 0,1 МПа. Сила давления на плоскую поверхность. Эпюра давления Общая сила давления со стороны жидкости на ограничивающую плоскую стенку равна произведению давления в центре тяжести стенки на величину смоченной поверхности: Р = рс ∙Sсм . (1.7) При этом, давление рс - это общее избыточное давление в центре тяжести. 6 Пример 1.6. (рис. 1.6)  Емкость заполнена жидкостью b   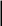 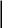 плотностью ρ = 800 кг/м3 до ро 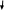    высоты Н = 4 м; угол наклона        стенки «В» равен α = 60о , шири-           на стенок b= 1 м; A hc На поверхности жидкости H давление ро = 10 кПа. CC   B Определить силу давления на обе 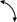 стенки.ρα Рис.1.6. Расчет. Давление в центре тяжести обеих стенок одинаково и равно рс = ро + ρghc= 20∙103 + 800∙9,8∙2 = 35,6 кПа. Сила давления на стенку «А» определится по ф. 1.7: РА = рс ∙(Н  b) = 35,6 ∙103∙4∙1 = 142,4 кН. b) = 35,6 ∙103∙4∙1 = 142,4 кН.Смоченная поверхность у стенки «В» больше: SB = SA/sinα= 4/0,866 = = 4,62 м2. Поэтому сила давления на нее значительнее: РВ = 164,4 кН. Эпюра давления – это график распределения давления по высоте стенки (рис. 1.7). Эпюра избыточного давления имеет, как правило, форму треугольника (AOB), полного давления – форму трапеции (AODC).     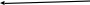    А po С  Рис. 1.7. Эпюры давления на стенки:   I- вертикальную III- наклонную      A     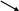  О            В D  BII O 7 Закон Архимеда. Используя зависимость 1.7, легко получить так наз. закон Архимеда: - На тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом.                 Vт На рис. 1.8 показано действие сил дав- ления на грани погруженного в жидкость тела кубической формы. Очевидно, что си- лы, действующие на боковые поверхности, Р1 h1 h2  равны по величине и противоположны по направлению, т.е. взаимно уравновешены. Сила Р1, действующая сверху, равна Р1 = ρgh1∙S, где S– площадь грани. Сила Р2, действующая снизу, равна ρ Р2 = ρgh2∙S. Р2 Разность между этими силами и Рис. 1.8 равна силе Архимеда: Fарх = Р2 – Р1 = ρgS (h2 – h1) = ρgVт, (1.8) где Vт – объем В зависимости от соотношения плотностей жидкости и тела возможны три варианта: - при ρ 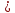 ρт – тело всплывает; ρт – тело всплывает;- при ρ 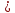 ρт - тело тонет; ρт - тело тонет;- при ρ = ρт – тело находится в покое (безразличном положении). Пример 1.7. Льдина, имеющая размеры а 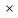 b b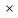 c = 20 c = 20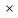 50 50 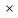 4 м , плавает в морской воде плотностью ρ = 1100 кг/м3; плотность льда ρл = 800 кг/м3. Какой груз можно разместить на льдине до ее полного погружения? 4 м , плавает в морской воде плотностью ρ = 1100 кг/м3; плотность льда ρл = 800 кг/м3. Какой груз можно разместить на льдине до ее полного погружения?Расчет: Объем льдины, погруженный в воду, равен Vпогр = 20∙50∙4∙(800/1100)  290 м3. 290 м3.Разность объемов льдины – полного и погруженного – обеспечит подъемную силу, равную весу груза: G = ρg(Vл  Vпогр) = 1100∙9,8∙(400 −290) = 11,86 МН. Vпогр) = 1100∙9,8∙(400 −290) = 11,86 МН.8 |
