Тема Основные понятия и величины в гидравлике Предмет и методы гидравлики, основные характеристики жидкостей
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
Тема 3. Гидравлические сопротивления и потери напора Вязкость жидкостей и ее оценка. Вязкость жидкостей и ее оценка.Вязкость – это внутреннее трение между жидкими частицами, препятствующее их относительному перемещению, обусловленное их межмолекулярным сцеплением.  И. Ньютон предположил, что ка- y сательное напряжение трения, возни-  кающее между жидкими слоями, про- Закон изменения скорости частиц  порционально градиенту скорости, т.е. производной скорости по высоте слоя Δy        (рис. 3.1):   τ = µ 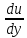 , (3.1) и , (3.1) и   где градиент скорости равен Δи 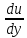 = lim = lim  ; ;при Δу→ 0 Рис. 3.1. - µ - коэффициент динамической вязкости, Па∙с. Сила вязкого трения будет равна Т = τ∙Sк = µ 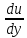 Sк , где Sк - площадь контакта. Sк , где Sк - площадь контакта.На практике удобнее пользоваться другой величиной – кинематическим коэффициентом вязкости ν = µ/ρ , м2/с. (3.2) Важность рассматриваемой характеристики – вязкости – в том, что она является основным источником гидравлических сопротивлений, вызывающих потери энергии потока. Гидравлические сопротивления и потери напора. Гидравлические сопротивления – это препятствия, вызывающие потери энергии потока; они подразделяются на два вида: - сопротивления по длине (линейные); - местные сопротивления (локальные). Названные сопротивления и вызывают соответствующие потери напора. Линейные потери напора. Эти потери вызываются в основном вязкостью жидкости (внутренним трением) и шероховатостью стенок (внешним трением) и вызывают снижение напора по длине трубопровода (рис. 3.2). 13            hl      Но1 Но2 d  υ  L Рис. 3.2. Линейные потери напора по длине трубы На участке трубы постоянного диаметра dи длиной Lпотери напора по длине равняются разности полных напоров на входе и выходе hl = Ho1 – Ho2  и определяются по закону Д а р с и: hl= λ 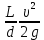 , (3.3) , (3.3)где λ – коэффициент сопротивления по длине, зависящий от режима течения жидкости и шероховатости стенок трубы, υ – скорость потока. Режим течения. Под р е ж и м о м т е ч е н и я понимается характер движения жидких частиц относительно друг друга. Существует два режима течения вязких жидкостей: - ламинарное (слоистое) течение, при котором частицы движутся параллельно друг другу, не перемешиваясь (например, на рис. 3.1); - турбулентное (вихревое) течение, когда частицы активно перемешиваются, перемещаясь поперек оси потока и образуя мелкие вихри. Критерием отличия режимов является ч и с л о Р е й н о л ь д с а: Re = 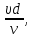 (3.4) (3.4)где ν – коэффициент кинематической вязкости. В технических расчетах принято считать, что если Re 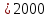 , то течение в трубе является ламинарным, в противоположном случае (Re , то течение в трубе является ламинарным, в противоположном случае (Re 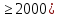 – турбулентным. То есть, ламинарное течение характерно для высоковязких жидкостей в узких каналах, турбулентное – для маловязких жидкостей в трубах (каналах) большого диаметра; при этом, при увеличении скорости течения ламинарное течение переходит в турбулентное. – турбулентным. То есть, ламинарное течение характерно для высоковязких жидкостей в узких каналах, турбулентное – для маловязких жидкостей в трубах (каналах) большого диаметра; при этом, при увеличении скорости течения ламинарное течение переходит в турбулентное.14 Пример 3.1. По трубе диаметром d = 10 мм течет минеральное масло вязкостью ν = 0, 1 см2/с со скоростью υ = 1,5 м/с. Определить режим течения жидкости. Расчет: Подставляем заданные величины в формулу (3.4), выразив их предварительно в единой размерности (СИ): Re = 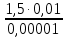 = 1500 , т.е. течение ламинарное. = 1500 , т.е. течение ламинарное.Найти: при какой скорости течения произойдет смена режима течения? Ответ: Режим течения сменится при Re 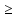 2000, значит, критическая скорость течения равна 2000, значит, критическая скорость течения равнаυкр =  = = 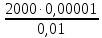 = 2 м/с. = 2 м/с.Определение коэффициента λ. При ламинарном течении коэффициент линейных потерь напора определяется по универсальной формуле: λЛАМ = 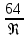 . (3.5) . (3.5) Так, в примере 3.1 коэффициент будет равен λЛАМ= 64/Re = 0,043, а линейные потери на участке трубы длиной L = 10 м составят: hl= λ 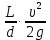 = = 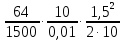 = 4,8 м масл. ст. = 4,8 м масл. ст.Чтобы перевести потери напора в потери давления нужно воспользоваться формулой: Δр = ρghl. (3.6) Допустим, плотность масла равна ρ = 800 кг/м3, тогда потери давления составят Δр = 800∙10∙4,8 = 38400 Па = 38,4 кПа. При турбулентном течении коэффициент λ зависит и от шероховатости стенок труб. Эта величина вводится в расчетные зависимости в форме так наз. относительной шероховатости - Δ/d, где Δ – средняя высота выступов шероховатости, d– внутренний диаметр трубы. Универсальная расчетная формула для турбулентного течения: λТУРБ = 0.11 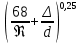 . (3.7) . (3.7)Кроме того, для расчетов широко используются графики и номограммы (см. Приложение I: график Мурина, график Альтшуля). 15 Местные потери напора.  Местные или локальные потери напора вызываются поворотами, сужениями и расширениями русла течения (трубопровода, канала), а также их комбинациями, что имеет место в технических местных сопротивлениях: вентилях, клапанах, задвижках и др.                  hм Рис. 3.3. Местное hм Рис. 3.3. Местноегидравлическое сопротивление ζ υ Потери напора в местных сопротивлениях определяются по формуле: hм = ζ 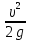 , (3.8) , (3.8)где ζ – коэффициент местного гидравлического сопротивления (МГС), определяемый опытным путем; для основных видов МГС составлены расчетные таблицы (Приложение II), в которых значения коэффициентов даны для развитого турбулентного течения. Пример 3.2. Коэффициент сопротивления вентиля обычно равняется ζв = 3. Каковы будут местные потери напора, если такой вентиль установить на трубе, рассмотренной в примере 3.1, для турбулентного течения (υ = 2 м/с)? Расчет: hм = ζ 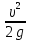 = 3 = 3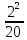 = 0,6 м масл. ст. = 0,6 м масл. ст.Потери давления соответственно будут Δр = ρghм = 800∙10∙0,6 = 4,8 кПа. Общие потери напора. Суммарные общие потери напора в трубопроводе определяются по закону сложения потерь: hw = hl + ∑hм = (λ  + ∑ζi)∙ + ∑ζi)∙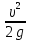 , (3.9) , (3.9)где ∑ζi– сумма коэффициентов всех местных сопротивлений, установленных на данном трубопроводе. 16 Уравнение Бернулли и напорная диаграмма. Основное уравнение потока вязкой жидкости – уравнение Бернулли – теперь записывается с учетом потерь: Z1 +  + +  = Z2 + = Z2 +  + +  + hw . (3.10) + hw . (3.10)Соответственно, и напорная диаграмма потока (рис. 3.4) будет отличаться от соответствующей диаграммы (рис. 2.6) для потока идеальной жидкости.   Z                            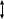     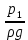 I hw I hw  II    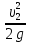  Z1 III  Z2 0 X Рис. 3.4. Напорная диаграмма потока вязкой жидкости Здесь: I– линия полного напора; II – линия пьезометрического напора; III – линия геометрического (геодезического) напора Примечание. Нетрудно заметить, что пространственная ориентация трубопровода ( наклон или подъем трубы ) влияет лишь на изменение геометрического напора; при этом гидростатический напор ( Z + p/ρg) остается неизменным. 17 |
