Фракталы. Реферат . Фракталы . Гоголев Р.. Фракталы. Множества Мандельброта и Жюлиа Автор Гоголев Руслан Игоревич Руденко Ирина Сергеевна Учитель информатики ноу Школаинтернат 25 оао ржд
 Скачать 0.51 Mb.
|
|
Региональная отраслевая техническая олимпиада учащихся профильных классов Научно-практическая конференция Фракталы. Множества Мандельброта и Жюлиа Автор: Гоголев Руслан Игоревич Руководитель: Руденко Ирина Сергеевна Учитель информатики НОУ «Школа-интернат №25 ОАО «РЖД» Секция: информатика г.Иркутск, 2015г. Содержание
Введение Когда большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических конфигураций, которое мы наблюдаем в мире растений и животных? Фракталы – подходящие средства для исследования поставленных вопросов. С образовательной точки зрения проекты, связанные с построением фракталов, имеют немало достоинств. ● Они достаточно просты в реализации (на базовом уровне). ● Они очень красивы (на любом уровне). ● Из них можно “выращивать” настоящие масштабные программные продукты. Но у этих проектов есть и недостатки. ● Алгоритмизация. ● Необходимо знакомство с комплексными числами ● Информация, которая лежит за рамками школьного курса. Цель: освоить технологию построения фракталов с помощью программной среды Lazarus и построить множества Мандельброта и Жюлиа. Задачи: ● Изучить «бесконечно самоподобные» геометрические фигуры; ● Построить множества Мандельброта и Жюлиа. ФракталФрактал – математическое множество, обладающее свойсвом самоподобия, то есть однородности в различных шкалах измерения. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев . Фракталы естественным образом возникают при изучении нелинейныхдинамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа. Пусть  — многочлен,  — комплексное число. Рассмотрим следующую последоватность Нас интересует поведение этой последовательности при стремлении  к бесконечности. Эта последовательность может:● стремиться к бесконечности, ● стремиться к конечному пределу, ● демонстрировать в пределе циклическое поведение, например:  ● вести себя хаотично, то есть не демонстрировать ни один из трёх упомянутых типов поведения. Множества значений , для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.Так, множество Жюлиа — множество точек бифуркации для многочлена  (или другой похожей функции), то есть тех значений , для которых поведение последовательности  может резко меняться при сколь угодно малых изменениях .Другой вариант получения фрактальных множеств — введение параметра в многочлен и рассмотрение множества тех значений параметра, при которых последовательность демонстрирует определённое поведение при фиксированном . Так, множество Мандельброта — это множество всех  , при которых для  и не стремится к бесконечности.Объекты, обладающие фрактальными свойствами, в природе● В живой природе ●Кораллы ●Морские звезды и ежи ●Морские раковины ●Цветы и растения (брокколи, капуста) ●Плоды (ананас) ●Кроны деревьев и листья растений ●В неживой природе: ●Границы географических объектов (стран, областей, городов) ●Береговые линии ●Горные хребты ●Снежинки ●Облака ●Молнии ●Образующиеся на стеклах узоры ●Кристаллы ●Сталактиты, сталагмиты, геликтиты. Множество Мандельброта Мно́жествоМандельброта — это множество таких точек c на комплексной плоскости, для которых итерационная последовательность  при  является ограниченной. То есть, это множество таких c, для которых существует такое действительное R, что неравенство |zn|<Rвыполняется при всех натуральных n.Множество Мандельброта является одним из самых известных фракталов, в том числе за пределами математики, благодаря своим цветным визуализациям. Его фрагменты не строго подобны исходному множеству, но при многократном увеличении определённые части всё больше похожи друг на друга 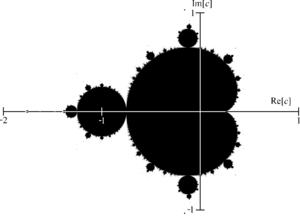 Множество Мандельброта  Множество Мандельброта в 3d Множество Жюлиа Мно́жество Жюлиа́- это множество точек, динамика в окрестности которых в определённом смысле неустойчива по отношению к малым возмущениям начального положения.В случае, если f — полином, рассматривают также заполненное множество Жюлиа — множество точек, не стремящихся к бесконечности. Обычное множество Жюлиа при этом является его границей .  Множество Жюлиа  Множество Жюлиа в 3d Практика Практическое применение Естественные науки[В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких кактурбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов). После создания кривой Коха было предложено использовать ее при вычислении протяженности береговой линии. РадиотехникаФрактальные антенныИспользование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск. ИнформатикаСжатие изображенийСуществуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранитьсжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили. Компьютерная графикаФракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см.Генератор фракталов (программа). Децентрализованные сетиСистема назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети. Экономика и финансыА. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс.Заключение Список литературы |