задачи по ла. задачи (часть 1). 1 Является ли линейным пространством а пустое множество
 Скачать 471.66 Kb. Скачать 471.66 Kb.
|
|
1 Является ли линейным пространством: а) пустое множество; б) множество, состоящее из одного нулевого элемента? 2 Можно ли определить во множестве из двух элементов операции сложения и умножения на число так, чтобы это множество стало линейным пространством? 3 Выяснить, является ли линейным пространством данное множество векторов из п-мерного пространства, и если является, найти его размерность: 1) множество векторов, все координаты которых равны между собой; 2) множество векторов, первая координата которых равна 0; 3) множество векторов, сумма координат которых равна 0; 4) множество векторов, сумма координат которых равна 1; 5) множество векторов плоскости, параллельных данной прямой; 6) множество векторов трехмерного пространства, перпендикулярных данной прямой; 7) множество векторов плоскости, по модулю не превосходящих 1; 8) множество векторов плоскости, образующих угол α с данной прямой (0 90 ) . 4 Доказать, что множество матриц размера m×п образует линейное пространство относительно обычных операций сложения матриц и умножения матрицы на число. Найти размерность и базис этого пространства. 6 Выяснить, является ли данное множество квадратных матриц порядка п линейным пространством, и если является, найти его размерность: 1) множество матриц с нулевой первой строкой; 2) множество диагональных матриц; 3) множество верхних треугольных матриц; 4) множество вырожденных матриц. 7 Выяснить, образует ли данное множество функций на произвольном отрезке [a, b] линейно пространство относительно обычных операций сложения и умножения на число: 1) множество функций, непрерывных на [a, b]; 2) множество функций, дифференцируемых на [a, b]; 3) множество функций, интегрируемых по Риману на [a, b]; 4) множество функций, ограниченных на [a, b]; 6) множество функций, неотрицательных на [a, b]; 7) множество функций таких, что f (a) 0 ; 8) множество функций таких, что f (a) 1; 10) множество функций, монотонно возрастающих на [a, b]; 11) множество функций, монотонных на [a, b]. 8 Доказать, что при любом натуральном п данное множество функций образует конечномерное линейное пространство; найти размерность и указать базис этого пространства: множество многочленов степени не выше п; 2) множество четных многочленов степени не выше п; 3) множество нечетных многочленов степени не выше п; 12 а) Пусть в некотором подпространстве размерности k введен базис. По Утверждению 2 его можно дополнить до базиса в исходном пространстве. Какие координаты будут иметь векторы подпространства в таком базисе? б) Равенство нулю определенных компонент вектора можно рассматривать как систему линейных уравнений, задающую подпространство. Составить систему уравнений, определяющую линейную оболочку данной системы столбцов: 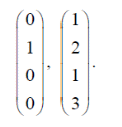 1. Найти размерность и базис линейной оболочки системы многочленов (1 t)3 , t3 , 1, t t2 . 1. Является ли базисом пространства R3 система векторов: 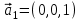 , , 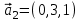 , , 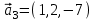 ; ;1. Является ли базисом пространства R3 система векторов 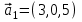 , , 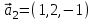 ; ;1.Является ли базисом пространства R3 система векторов 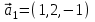 , , 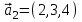 , , 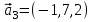 , , 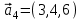 . .1. Найти размерность и базис пространства решений однородной системы: 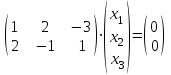 ; ; 1.Найти размерность и базис пространства решений однородной системы: 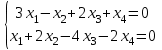 ; ;1.Найти размерность и базис пространства решений однородной системы: 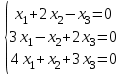 ; ; 1.Найти размерность и базис пространства решений однородной системы: 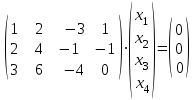 ; ;1.Найти размерность и базис пространства решений однородной системы: 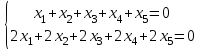 . .1. Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и лежащих на прямой 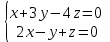 ; ;1.Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и перпендикулярных прямой 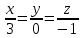 ; ;1.Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и лежащих в плоскости 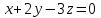 ; ;1.Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и перпендикулярных плоскости 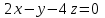 . .1. Найти размерность и указать какой-либо базис пространства многочленов степени не выше n; 1.Найти размерность и указать какой-либо базис пространства квадратных матриц порядка n; 1.Найти размерность и указать какой-либо базис пространства прямоугольных матриц размера 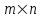 ; ;1. Найти размерность и указать какой-либо базис пространства симметричных матриц порядка n; 1. Найти размерность и указать какой-либо базис пространства диагональных матриц порядка n. 1.Доказать, что система 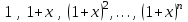 образует базис пространства многочленов степени не выше n. образует базис пространства многочленов степени не выше n.1. Найти размерность и указать какой-либо базис пространства положительных чисел, в котором сумма произвольных чисел 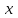 и и 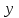 вычисляется как вычисляется как 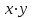 , а произведение вещественного числа , а произведение вещественного числа 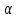 на произвольное положительное число на произвольное положительное число 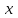 вычисляется как вычисляется как 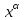 . .1. Построить матрицу перехода 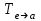 от базиса от базиса 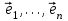 к базису к базису 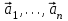 и матрицу обратного перехода, если векторы и матрицу обратного перехода, если векторы 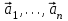 в базисе в базисе 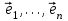 имеют координаты имеют координаты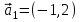 , ,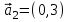 ; ;1.Построить матрицу перехода 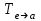 от базиса от базиса 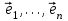 к базису к базису 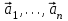 и матрицу обратного перехода, если векторы и матрицу обратного перехода, если векторы 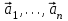 в базисе в базисе 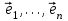 имеют координаты имеют координаты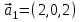 , ,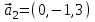 , ,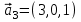 . .1. Найти матрицу перехода от базиса 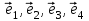 к базису к базису 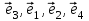 ; ;1. Найти матрицу перехода от базиса 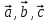 к базису к базису 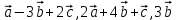 . .1. Дана матрица перехода 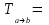 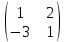 от базиса 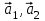 к базису к базису 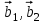 . Найти координаты вектора . Найти координаты вектора 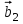 в базисе в базисе 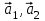 ; ; 1. Дана матрица перехода 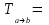 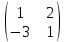 от базиса 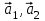 к базису к базису 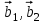 . Найти координаты вектора . Найти координаты вектора 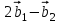 в базисе в базисе 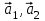 ; ;1. Дана матрица перехода 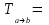 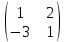 от базиса 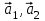 к базису к базису 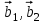 . Найти координаты вектора . Найти координаты вектора 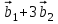 в базисе в базисе 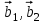 ; ;1. Дана матрица перехода 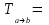 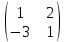 от базиса 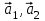 к базису к базису 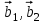 . Найти координаты вектора . Найти координаты вектора 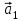 в базисе в базисе 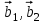 ; ;1. Дана матрица перехода 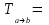 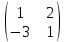 от базиса 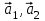 к базису к базису 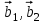 . Найти координаты вектора . Найти координаты вектора 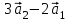 в базисе в базисе 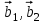 1. Дана матрица перехода 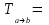 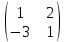 от базиса 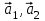 к базису к базису 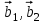 . Найти координаты вектора . Найти координаты вектора 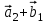 в базисе в базисе 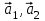 . .1. Используя матрицу перехода от базиса к базису, найти координаты вектора 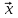 в базисе в базисе 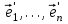 , если в базисе , если в базисе 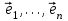 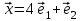 , ,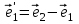 , ,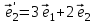 ; ;1. Используя матрицу перехода от базиса к базису, найти координаты вектора 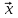 в базисе в базисе 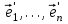 , если в базисе , если в базисе 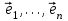 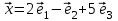 , , 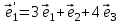 , , 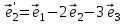 , , 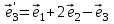 . .1. Построить матрицу перехода 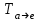 от базиса от базиса 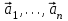 к базису к базису 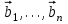 по данным разложениям векторов по данным разложениям векторов 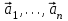 и и 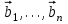 в базисе в базисе 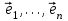 : : 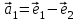 , ,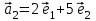 , ,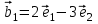 , ,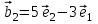 ; ;1. Используя матрицу перехода от базиса к базису, найти координаты вектора 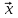 в базисе в базисе 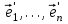 , если в базисе , если в базисе 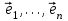 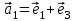 , , 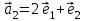 , , 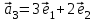 , , 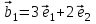 , , 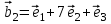 , , 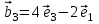 . .Построить матрицу перехода 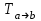 от базиса от базиса 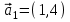 , , 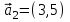 к базису к базису 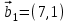 , ,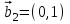 и матрицу обратного перехода и матрицу обратного перехода 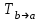 . . 1. Построить матрицу перехода от базиса 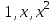 к базису к базису 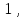 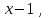 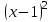 в пространстве многочленов степени не выше в пространстве многочленов степени не выше 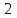 . .1. В пространстве многочленов степени не выше 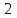 найти разложение вектора найти разложение вектора 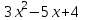 по базису по базису 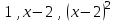 . .Найти размерность и какой-нибудь базис подпространства, порожденного векторами 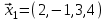 , , 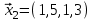 , , 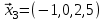 , , 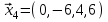 , , 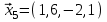 . .1. Найти размерность и какой-либо базис линейной оболочки векторов 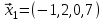 , ,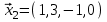 , ,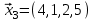 , ,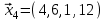 , ,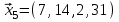 . .1. Является ли подпространством в указанном пространстве множество векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R2; 1. Является ли подпространством в указанном пространстве множество диагональных матриц в пространстве квадратных матриц того же порядка; 1. Является ли подпространством в указанном пространстве множество невырожденных матриц в пространстве симметричных матриц того же порядка; 1. Является ли подпространством в указанном пространстве множество дифференцируемых на интервале 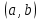 функций в пространстве функций, непрерывных на отрезке функций в пространстве функций, непрерывных на отрезке 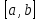 . .1. Найти размерность и какой-либо базис подпространства решений однородной системы: 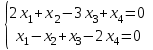 ; ; 1. Найти размерность и какой-либо базис подпространства решений однородной системы: 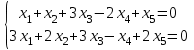 ; ;1. Найти размерность и какой-либо базис подпространства решений однородной системы: 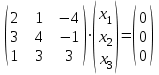 . .Найти размерность суммы и пересечения подпространств, порожденных векторами 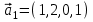 , ,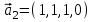 и и 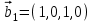 , , 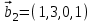 . Является ли эта сумма прямой суммой? . Является ли эта сумма прямой суммой?1. Найти размерность суммы и пересечения линейных оболочек векторов 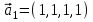 , ,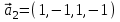 , ,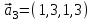 и и 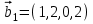 , , 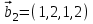 , ,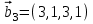 . Является ли их cумма прямой? . Является ли их cумма прямой?1. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 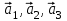 и и 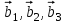 , если , если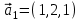 , ,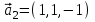 , ,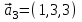 , ,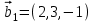 , , 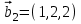 , , 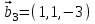 ; ;1. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 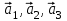 и и 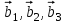 , если , если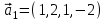 , ,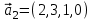 , ,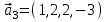 , , 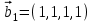 , , 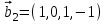 , ,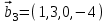 . .Является ли прямой сумма этих подпространств? 1. Найти базис суммы и пересечения линейных оболочек 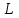 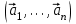 и и 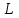 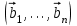 , если , если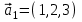 , ,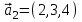 , ,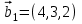 , ,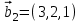 ; ;Является ли прямой сумма этих подпространств? 1. Найти базис суммы и пересечения линейных оболочек 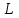 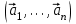 и и 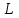 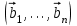 , если , если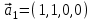 , ,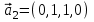 , ,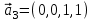 , , 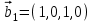 , , 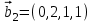 , ,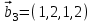 . .Является ли прямой сумма этих подпространств? 1.Ортогонализировать систему векторов: 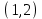 , ,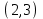 ; ; 1.Ортогонализировать систему векторов: 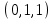 , ,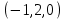 , ,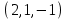 ; ;1.Ортогонализировать систему векторов: 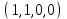 , ,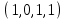 , ,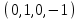 . .1. Построить ортонормированный базис линейной оболочки векторов: 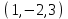 , ,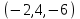 ; ; 1. Построить ортонормированный базис линейной оболочки векторов: 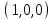 , ,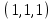 , ,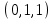 ; ;1. Построить ортонормированный базис линейной оболочки векторов: 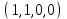 , ,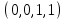 , ,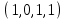 , ,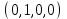 . .1. Дополнить до ортогонального базиса пространства Еn систему векторов: а) 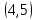 ; б) ; б) 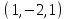 , ,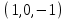 ; ;1. Дополнить до ортогонального базиса пространства Еn систему векторов: 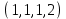 , ,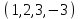 , ,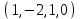 ; ; 1. Дополнить до ортогонального базиса пространства Еn систему векторов: 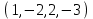 , ,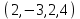 . .1. Дополнить до ортонормированного базиса пространства Еnсистему векторов: 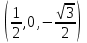 ; ; 1. Дополнить до ортонормированного базиса пространства Еnсистему векторов: 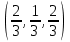 , ,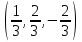 ; ;1. Дополнить до ортонормированного базиса пространства Еnсистему векторов: 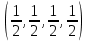 , ,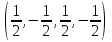 . .1. Построить матрицу Грама для системы векторов: а) 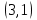 , ,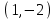 ; б) ; б) 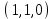 , ,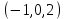 , ,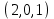 ; ;1. Построить матрицу Грама для системы векторов: 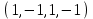 , ,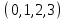 . .1. Вычислить скалярное произведение векторов 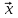 и и 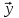 , заданных своими координатами в базисе , заданных своими координатами в базисе 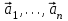 , если , если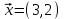 , ,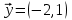 , ,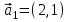 , ,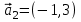 ; ; 1. Вычислить скалярное произведение векторов 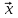 и и 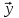 , заданных своими координатами в базисе , заданных своими координатами в базисе 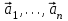 , если , если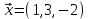 , ,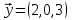 , ,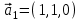 , ,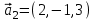 , , 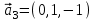 . .1. Вычислить длины векторов 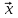 , ,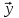 и угол между ними, если даны следующие разложения по базису и угол между ними, если даны следующие разложения по базису 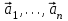 и ортонормированному базису и ортонормированному базису 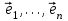 : :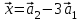 , ,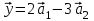 , ,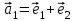 , ,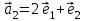 ; ;1. Вычислить длины векторов 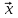 , ,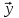 и угол между ними, если даны следующие разложения по базису и угол между ними, если даны следующие разложения по базису 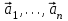 и ортонормированному базису и ортонормированному базису 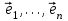 : :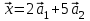 , ,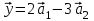 , ,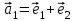 , ,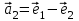 ; ;1. Вычислить длины векторов 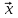 , ,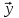 и угол между ними, если даны следующие разложения по базису и угол между ними, если даны следующие разложения по базису 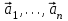 и ортонормированному базису и ортонормированному базису 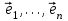 : :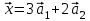 , ,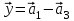 , ,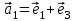 , ,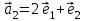 , , 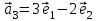 . .1. Найти площадь параллелограмма, построенного на векторах: а) 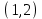 , ,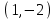 ; б) ; б) 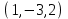 , ,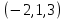 ; ;1. Найти площадь параллелограмма, построенного на векторах 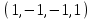 , ,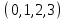 . .1. Вершины треугольника 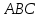 заданы своими координатами: заданы своими координатами: 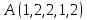 , ,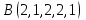 , ,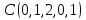 . Найти . Найтиа) площадь треугольника 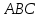 ; ;б) длину высоты, опущенной из вершины 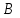 . .1. Найти объем параллелепипеда, построенного на векторах: 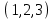 , ,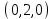 , ,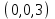 ; ;1. Найти объем параллелепипеда, построенного на векторах: 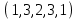 , ,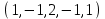 , ,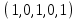 . .Основание параллелепипеда, построенного на векторах 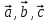 , лежит в плоскости векторов , лежит в плоскости векторов 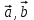 . Найти высоту параллелепипеда, проведенную к основанию, если в ортонормированном базисе . Найти высоту параллелепипеда, проведенную к основанию, если в ортонормированном базисе 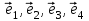 справедливо разложение справедливо разложение 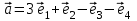 , , 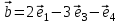 , , 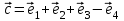 . .1. Вершины пирамиды 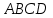 заданы своими координатами: заданы своими координатами: 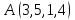 , , 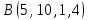 , , 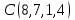 , ,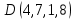 . Найти объем пирамиды, длину высоты, опущенной из вершины . Найти объем пирамиды, длину высоты, опущенной из вершины 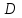 на основание на основание 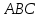 , и угол наклона бокового ребра , и угол наклона бокового ребра 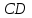 к плоскости основания. к плоскости основания. 1. Найти размерность и базис ортогонального дополнения к линейной оболочке векторов: 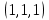 , ,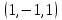 ; ; 1. Найти размерность и базис ортогонального дополнения к линейной оболочке векторов: 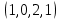 , ,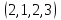 , ,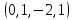 ; ;1. Найти размерность и базис ортогонального дополнения к линейной оболочке векторов: 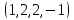 , ,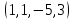 , ,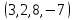 . .1. Найти размерность и базис ортогонального дополнения к подпространству, заданному системой 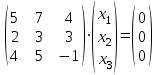 ; ; 1. Найти размерность и базис ортогонального дополнения к подпространству, заданному системой 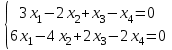 ; ;1. Найти размерность и базис ортогонального дополнения к подпространству, заданному системой 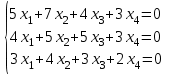 Найти ортогональную проекцию 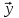 и ортогональную составляющую и ортогональную составляющую 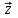 вектора вектора 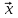 относительно подпространства, порожденного векторами 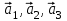 , если , если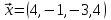 , ,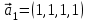 , ,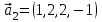 ; ;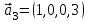 ; ;Найти ортогональную проекцию 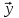 и ортогональную составляющую и ортогональную составляющую 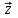 вектора вектора 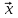 относительно подпространства, порожденного векторами 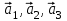 , если , если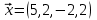 , ,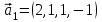 , ,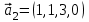 ; ;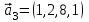 . .1. Найти ортогональную проекцию 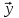 и ортогональную составляющую и ортогональную составляющую 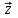 вектора вектора 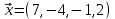 относительно подпространства, заданного системой относительно подпространства, заданного системой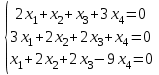 . .1. Найти ортогональную проекцию 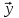 и ортогональную составляющую и ортогональную составляющую 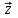 вектора вектора 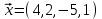 относительно ортогонального дополнения к линейной оболочке векторов относительно ортогонального дополнения к линейной оболочке векторов 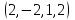 , ,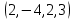 . .1.Найти расстояние от вектора 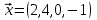 до подпространства L и угол между ними, если до подпространства L и угол между ними, если 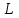 задано системой задано системой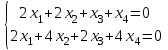 . .1. Найти расстояние от вектора 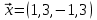 до линейной оболочки до линейной оболочки 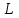 векторов векторов 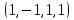 , ,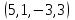 и угол между и угол между 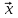 и и 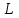 . . 1. Найти угол между вектором 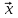 и подпространством, порожденным векторами и подпространством, порожденным векторами 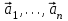 , если , если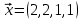 , ,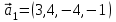 , ,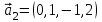 ; ; 1. Найти угол между вектором 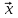 и подпространством, порожденным векторами и подпространством, порожденным векторами 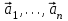 , если , если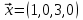 , ,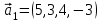 , ,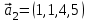 ; ;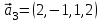 . . |
