Теория множест. Вариант 2 Теория множеств

• Название: Вариант 2 Теория множеств
• Дата: 02.05.2023
• Размер: 138.59 Kb.
• Имя файла: Теория множест.docx
• Тип: Решение; #1103262

Вариант 2

Теория множеств

№ 1. Найти все подмножества множества {1, 2, 3 }.

Решение:

Выпишем одноэлементные подмножества: {1}, {2}, {3}, затем двухэлементные: {1, 2}, {1, 3}, {2, 3}, трехэлементные: {1, 2, 3} и множество, не содержащее ни одного элемента (пустое множество) – .

Количество подмножеств множества, состоящего из n элементов равно . В нашем примере множество состоит из трех элементов, значит количество подмножеств равно   =8.
№ 2. А – множество студентов в одной из групп факультета, а В – множество отличников на факультете. Какие множества студентов описывают множества: А В; А\В; В\А?

Решение:

Пересечением множеств А и В называется множество А В, состоящее из всех элементов, которые принадлежат одновременно множеству А и В:

А В = {х | х А и х В}.

Тогда А В – это множество отличников данной группы.

Разностью множеств A и B называется множество А\В элементов, принадлежащих A и не принадлежащих B.

Тогда А\В – множество студентов данной группы, не являющихся отличниками.

В\А – множество отличников факультета за исключением отличников данной группы.
№ 3. Множества А и В есть подмножества множества I (рис.)


А

В

I


Заштриховать на рис. следующие множества: 1) А В; 2) А В; 3) ; 4)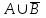

Решение:

1) А В – объединение множеств А и В (все точки обоих множеств):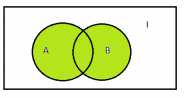



2) А В – пересечение множеств А и В (общие точки двух множеств):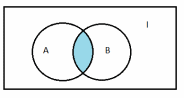



3) – дополнение множества А (точки, не принадлежащие множеству А):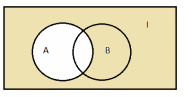



4) 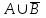– объединение множества А и дополнения множества В:



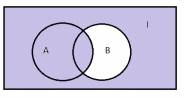№ 4. Дано множество К={a;b;{c,d};{e;f;m}}. Определите, какие из следующих высказываний истинны и почему:

а) {a;{c;d}} K;

б) {c;d} K;

в){{c;d}} K;

г){c;d} K.

Решение: Если любой элемент множества А принадлежит так же и множеству В, то А называют подмножеством В. Записывают А  В. Знак  называют знаком включения. Знак  обозначает принадлежность какого-либо элемента к множеству. Поэтому высказывания а), в) и г) являются истинными, а высказывание б) – ложным. Действительно, множество {a;{c;d}}, состоящее из двух элементов a и {c;d} является подмножеством В. Множество {{c;d}}, состоящее из одного элементa {c;d} является подмножеством множества К. Элемент {c;d} принадлежит множеству К. А вот множество {c;d}, состоящее из двух элементов с и d не является подмножеством множества К, потому что отдельные элементы с и d не являются элементами множества К.

№ 5. Найдите разность множеств P и S, если:

P={x|x Z, -4 x 6} , S={ x|x N, 3 x 10}. Здесь Z – множество целых чисел, N - множество натуральных чисел.

Решение:

Разностью множеств P и S называется множество элементов, принадлежащих P и не принадлежащих S. Обозначают P\S и читают "разность P и S". .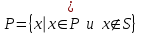



Получаем, что разность множеств P и S – это все точки отрезка за исключением четырех точек х = 3,4,5,6.

№ 6. Найдите дополнение к множеству В до множества А, если

а) А={11;12;43;54;7}, B={7;12}.

Решение:



Это множество называют дополнением множества   до множества  . (только когда множество В полностью принадлежит множеству А).

Тогда .

б) А – множество учащихся некоторого класса; В – множество отличников в этом классе.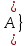

– множество учащихся данного класса, не являющихся отличниками.

№ 7. Даны множества А= {a,b,c},B={1,2} C={2,3,4}.

Запишите множества 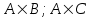и .

Решение:

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А  В. Таким образом А  В = {(x;y) | x  A, y  B}. Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

А  В={(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}.

А  С={(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4), (c, 2), (c, 3), (c, 4)}.

В  С={(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.

№ 8. Запишите множество различных цифр в записи числа 235 535. Запишите кортеж цифр этого числа. Какова длина этого кортежа?

Решение:

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.

Множество различных цифр в записи числа 235 535 имеет вид: {2,3,5}.

Кортеж числа 235 535 имеет вид (2; 3; 5; 5; 3; 5). Его длина равна 6.

№ 9. Пусть Х={”мама”;“папа”;“рама”;“яма”}; Y={а,м,р,п,я}. Составьте декартово произведение . Отметьте в нем пары, связанные соответствием «В слово х входит буква у».

Решение:

Декартово произведение = { (”мама”, а), (”мама”, м), (”мама”, р), (”мама”, п), (”мама”, я), (“папа”, а), (“папа”, м), (“папа”, р), (“папа”, п), (“папа”, я), (“рама ”, а), (“рама ”, м), (“рама ”, р), (“рама ”, п), (“рама ”, я), (“яма ”, а), (“яма ”, м), (“яма ”, р), (“яма ”, п), (“яма ”, я)}.

Выделим подчеркиванием среди выписаных пары, связанные соответствием «В слово х входит буква у».

№10. А – множество прямых на плоскости. Выясните, какие из следующих отношений в множесве А являются отношениями эквивалентности.

а) « прямая а перпендикулярна прямой b»

б) “ прямая а паралельна прямой b”

в) “ прямая а пересекает прямую b”.

Решение:

Отношение эквивалентности ( ) на множестве   — это бинарное отношение, для которого выполнены следующие условия:

1. 
   Рефлексивность:   для любого   в  ,
   
2. 
   Симметричность: если  , то  ,
   
3. 
   Транзитивность: если   и  , то  .
   

а) «прямая а перпендикулярна прямой b» не является отношением эквивалентности, т.к. это отношение не рефлексивно: прямая не является перпендикулярной сама себе.

б) “ прямая а паралельна прямой b” - это отношение эквивалентности:
1) а параллельна а (рефлексивность)
2) а параллельна b ⇒ b параллельна а (симметричность)
3) а параллельна b, b параллельна с ⇒ а параллельна с (транзитивность).

в) “прямая а пересекает прямую b” – не является отношением эквивалентности, т.к. это отношение не транзитивно: если а параллельна с, а b пересекает обе прямые, то (a,b) и (b,с) находятся в отношении, а (а,с) - нет.


№11. На рис. изображены графы различных соответствий. Какие из этих соответствий являются отображениями?

X Y X Y X Y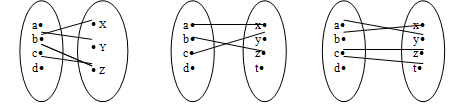



Решение:

Отображением (функцией)  f из A в B называется правило, которое каждому элементу множества A сопоставляет некоторый элемент множества B. 

Отношение между элементами множеств Х и Y называется отображением ХвY, если каждому элементу х из множества Хсоответствует только один элемент множества Y. Этот элемент называют образом элементах при данном отображении:  f(x).На графе такого отображения из каждой точки множества Х будет выходить только одна стрелка.

Следовательно, отображением является только второе соответствие, т.к. у него каждому элементу из Х соответствует только один элемент Y (ax, bz, cy). Соответствия на первом и третьем графах не являются отображениями, так как некоторым элементам Х соответствуют по два-три элемента Y.